|
| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants | |
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 27 Fév 2011, 17:02 Dim 27 Fév 2011, 17:02 | |
| - M.Marjani a écrit:
- Je ne vois pas où l'erreur si f(2x)=f(x^2) , 2x ou x^2 n'appartiennent pas à X?
L'erreur est de prendre x=3, car x est censé être supérieur à 4. | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 27 Fév 2011, 18:00 Dim 27 Fév 2011, 18:00 | |
| - Dijkschneier a écrit:
Problème 67 : (** : deux étoiles)
Soient E,F,G et H quatre ensembles, f une application de E vers F et g une application de G vers H.
On considère l'application k de 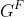 vers vers 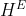 définie par : définie par : =g\circ%20u%20\circ%20f) où la notation où la notation 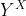 désigne l'ensemble des fonctions définies sur X et à valeurs dans Y. désigne l'ensemble des fonctions définies sur X et à valeurs dans Y.
i) Montrer que si f est surjective et g est injective, alors k est injective
ii) Montrer que si f est injective et g est surjective, alors k est surjective.
Vous ne devez proposer une solution que si vous avez la réponse à i) et à ii)
Solution au problème 67 :i) Soient u et v de G^F (c'est-à-dire deux fonctions définies sur F et à valeurs dans G) telles que k(u)=k(v) =k(v)%20&\Rightarrow%20g\circ%20u%20\circ%20f%20=%20g%20\circ%20v%20\circ%20f%20\\%20&\Rightarrow%20\forall%20x%20\in%20E%20:%20g\circ%20u%20\circ%20f(x)%20=%20g%20\circ%20v%20\circ%20f(x)%20\\%20&\Rightarrow%20\forall%20x%20\in%20E%20:%20u%20\circ%20f(x)%20=%20v%20\circ%20f(x)%20\text{%20(car%20g%20est%20injective)}%20 (1) \end{align*}) Soit 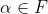 et 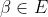 tel que f(beta)=alpha (ce beta existe car f est surjective) Pour x=beta dans (1), il vient u(f(beta))=v(f(beta)), et donc u(alpha)=v(alpha). Donc pour tout alpha de F : u(alpha)=v(alpha) Ce qui veut dire que u=v. ii) Soit y de H^E. On recherche x de G^F tel que k(x)=y. k(x)=y <===> pour tout a de E : g(x(f(a)))=y(a) On construit la fonction x de cette manière : - x est définie sur F et à valeurs dans G - si alpha appartient à f(E), alors on définit x(alpha)=b, tel que b appartienne à G et est tel que g(b)=y(b') (ce b existe car g est surjective), et tel que b' appartienne à E et est tel f(b')=alpha (ce b' existe car alpha appartient à f(E)) - si alpha n'appartient pas à f(E), alors on choisit pour x(alpha) n'importe quelle valeur (par exemple, une constante) Vérifions que cette fonction x est bonne : Soit a de E. On a : g(x(f(a)))=g(b)=y(b'), car f(a) appartient à f(E) Or, d'après la définition de b', on a aussi : f(b')=f(a) Par injectivité de f, on a alors : b'=a Par conséquent, on a bien : g(x(f(a)))=y(a). Ainsi, pour tout a de E, g(x(f(a)))=y(a), et donc : 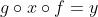 , et donc %20=%20y) , ce qui montre bien la surjectivité de k. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 27 Fév 2011, 18:48 Dim 27 Fév 2011, 18:48 | |
| - Mehdi.O a écrit:
- J'ai une solution que j'estime douteuse, mais je l'ai relu plusieurs fois, je n'ai trouvé aucune erreur. La voici :
Tout d'abord puisque Le cercle est inscrit dans le carré ABCD, donc E,F,G et H sont respectivement les milieux de [AB],[BC],[CD] et [AD].
Le quadrilatère NGFE est inscriptible, ainsi <MNG=<FNG=<GEF=45°.
D'autre part : <AMF=180°-<MAF-<MFA=180°-(90°-<GAD-<FAB)-(90°-<DFC-<AFB)=180°-(90°-22.5°-22.5°)-(180°-67.5°-67.5)=90°
Ainsi Le triangle MNG est rectangle, il s'ensuit qu'il est isocèle rectangle.
Donc K=MN²/2. Maintenant, nous avons : <NDG=<FDC=arctan(1V5),ainsi sin(<NDG)=sin(<MDG)=MG/DG=MN/DG=2MN/DC, donc MN²=DC²/4.sin²(<NDG)
il s'ensuit que S=8/(sin²(<NDG).K=8/(sin²(arctan(1/2)).K
ainsi n=40
CQFD  Très bien, sauf quelques fautes vers la fin. Je te reproche aussi le fait de sauter quelques étapes importantes. Franchement, ce n'était pas la question telle qu'elle est présentée. (La question était: démontrez que S=40K). Il y a un indice qui le montre: mon utilisation du terme "entier" au lieu de "réél". Mon prochain message, dans la rubrique "géométrie", sera consacré à un site d'où cet exercice est extrait. | |
|   | | yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 28 Fév 2011, 21:36 Lun 28 Fév 2011, 21:36 | |
| - Dijkschneier a écrit:
- nmo a écrit:
- Dijkschneier a écrit:
- Classique ET simple...
Comment tu as procédé?
Par ailleurs, je vais chercher un exercice à la hauteur. Si on définit la fonction f(x)=sqrt(20+sqrt(20-x)), alors notre équation n'est rien d'autre que f(f(x))=x, à résoudre dans [0,20]
Et on peut remarquer qu'il suffit de résoudre f(x)=x dans [0,20] puisque les points fixes de f sont aussi les points fixes de f(f(x)), et que le graphe de f(f(x)) coupe une seule fois la droite d'équation y=x. j'ai pas compris pk, pouvez vous un peu expliquer!je'en srai tres reconnaisant.merci d'avance amicalement  | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 01 Mar 2011, 18:21 Mar 01 Mar 2011, 18:21 | |
| @yasserito : il faut préciser ce que tu n'as pas compris.
@Mehdi.O : il me semble que c'est à toi de proposer le nouveau problème... | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 01 Mar 2011, 18:53 Mar 01 Mar 2011, 18:53 | |
| Problème 74 :
Trouvez toutes les fonctions définies sur IR et vérifiant :
f(x-f(y))=1-x-y
Je sais que c'est facile, mais je n'ai aucun bon problème à proposer
Dernière édition par Mehdi.O le Mar 01 Mar 2011, 19:13, édité 1 fois | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 01 Mar 2011, 19:01 Mar 01 Mar 2011, 19:01 | |
| Solution au problème 74 :
Soit f une fonction vérifiant l'EF.
Soit P(x,y) l'assertion : f(x-f(y))=1-x-y.
P(x+f(0),0) ==> f(x)=1-(x+f(0)-0=1-x-f(0)
Ainsi, f est de la forme : f(x)=1-x+c
Inversement, si f(x)=1-x+c, alors l'EF devient : 1-(x-f(y))+c = 1-x-y
<=> 1-x+f(y)+c=1-x-y
<=> f(y)+c = -y
<=> f(y) = -y - c
<=> 1-y+c = -y-c
<=> 2c=-1
<=> c=-1/2
Par suite : f(x)=1/2 - x
Synthèse :
La seule solution à l'EF est la fonction : x -> 1/2 -x
Dernière édition par Dijkschneier le Mar 01 Mar 2011, 19:27, édité 2 fois | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 01 Mar 2011, 19:18 Mar 01 Mar 2011, 19:18 | |
| - Dijkschneier a écrit:
- Solution au problème 74 :
Soit f une fonction vérifiant l'EF.
Soit P(x,y) l'assertion : f(x-f(y))=1-x-y.
P(x+f(0),0) ==> f(x)=1-(x+f(0)-0=1-x-f(0)
Ainsi, f est de la forme : f(x)=1-x+c
Inversement, si f(x)=1-x+c, alors l'EF devient : 1-(x-f(y))+c = 1-x-y
<=> 1-x+f(y)+c=1-x-y
<=> f(y)+c = 1-y
<=> f(y) = 1-y-c
<=> 1-y+c = 1-y-c
<=> c=0
Synthèse :
La seule solution à l'EF est la fonction : x -> 1-x
Problème 75 : Ton résultat est faux, à cause d'uen faute d'inattention : 1-x+f(y)+c=1-x-y<=>f(y)+c=-y<=>1-y+c+c=-y<=>c=-1/2 ainsi f(x)=1/2-x ce qui est une solution bien sûr  | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 01 Mar 2011, 19:19 Mar 01 Mar 2011, 19:19 | |
| A toi l'honneur, de poster un exercice  | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 01 Mar 2011, 19:29 Mar 01 Mar 2011, 19:29 | |
| Merci, j'ai corrigé.
Problème 75 : (* : une étoile)
Soient a et b des entiers naturels tels que a>b, et x,y et z des entiers naturels.
Montrer que si xyz=2a(a²+3b²), alors x et y et z ne peuvent pas être tous les trois égaux. | |
|   | | az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 01 Mar 2011, 19:51 Mar 01 Mar 2011, 19:51 | |
| voici un exercice   :  donner la valeur de x + y | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 01 Mar 2011, 19:56 Mar 01 Mar 2011, 19:56 | |
| Cher az360,
tu dois lire d'abord les règles, on ne doit aps poster des exerices arbitrairement car cela nuit le bon cours de ce topic.
En ce qui concerne ton probleme, il est classique :
En multipliant respectivement par (V(x²+1)-x) et (V(y²+1)-y) on trouve y+V(y²+1)=V(x²+1)-x et x+V(x²+1)=V(y²+1)-y en sommant on trouve 2(x+y)=0, donc x+y=0
CQFD | |
|   | | az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 01 Mar 2011, 20:04 Mar 01 Mar 2011, 20:04 | |
| ^^ je suis désolé Mehdi.O  . | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 06 Mar 2011, 19:45 Dim 06 Mar 2011, 19:45 | |
| - Dijkschneier a écrit:
- Merci, j'ai corrigé.
Problème 75 : (* : une étoile)
Soient a et b des entiers naturels tels que a>b, et x,y et z des entiers naturels.
Montrer que si xyz=2a(a²+3b²), alors x et y et z ne peuvent pas être tous les trois égaux. Solution 75 :Soit a,b les naturels qui vérifient l'énoncé. On suppose que x =y =z et démontrant que le cube d'un naturel non nul ne peut en aucun cas égale à 2a(a²+3b²). Si x^3 = 2a(a²+3b²) Alors x est congru à 0 modulo 2 cela implique : \Leftrightarrow%208k^3=6a^3-6a^3+2a(a^2+3b^2)) (k^2+ak+a^2)=3a(a-b)(a+b)) D'autre coté, =3a(a^2-b^2)\Rightarrow%20\exists%20m\in%20\mathbb{N*}\:%20/\:%20a(a^2-b^2)=4m) donc a,b ont la même parité. Et si ((2k%27+1)^2+3(2m%27+1)^2)) équiv (2(2k%27^2+2k+2m^2+2m)+1)) qui est bien une contradiction, donc a,b sont tous les deux pairs. Cela conduit à \in%20\mathbb{(N*)}^2\:%20/\:%204k^3=2k%27(4k%27^2+3*4l^2)\Leftrightarrow%20k^3=2(k%27^2+3l^2)) donc k pair et k'>l, on remarquera qu'on peut répéter cette phase n fois, et que x^3 =8k^3 =8*(8(k'')^3) =... jusqu'à k''_{n}£{0,1,8} donc a^2 = 4k'^2 = ... = (2^{2n})*k'{n} et si veut-on qu'il sera juste pour x^3 on doit appliquer une disjonction de cas sur k''_{n}£{0,1,8} pour trouver dans chaque fois une contradiction. Ainsi l'hypothèse est fausse. En attendant d'une confirmation, voici un nouveau problème. Problème 76 : *Montrer que 798 devise y*x^{19}-x*y^{19} quelque soit x,y des entiers naturels . | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 11 Mar 2011, 17:12 Ven 11 Mar 2011, 17:12 | |
| - M.Marjani a écrit:
- Cela conduit à
\in%20\mathbb{(N*)}^2\:%20/\:%204k^3=2k%27(4k%27^2+3*4l^2)\Leftrightarrow%20k^3=2(k%27^2+3l^2)) donc k pair et k'>l, on remarquera qu'on peut répéter cette phase n fois, et que x^3 =8k^3 =8*(8(k'')^3) =... jusqu'à k''_{n}£{0,1,8} donc a^2 = 4k'^2 = ... = (2^{2n})*k'{n} et si veut-on qu'il sera juste pour x^3 on doit appliquer une disjonction de cas sur k''_{n}£{0,1,8} pour trouver dans chaque fois une contradiction. Ainsi l'hypothèse est fausse. donc k pair et k'>l, on remarquera qu'on peut répéter cette phase n fois, et que x^3 =8k^3 =8*(8(k'')^3) =... jusqu'à k''_{n}£{0,1,8} donc a^2 = 4k'^2 = ... = (2^{2n})*k'{n} et si veut-on qu'il sera juste pour x^3 on doit appliquer une disjonction de cas sur k''_{n}£{0,1,8} pour trouver dans chaque fois une contradiction. Ainsi l'hypothèse est fausse. Cela me rappelle bien ce type de raisonnement: http://fr.wikipedia.org/wiki/M%C3%A9thode_de_descente_infinie. Je pense que ton raisonnement est bon. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 11 Mar 2011, 17:58 Ven 11 Mar 2011, 17:58 | |
| - nmo a écrit:
- M.Marjani a écrit:
- Cela conduit à
\in%20\mathbb{(N*)}^2\:%20/\:%204k^3=2k%27(4k%27^2+3*4l^2)\Leftrightarrow%20k^3=2(k%27^2+3l^2)) donc k pair et k'>l, on remarquera qu'on peut répéter cette phase n fois, et que x^3 =8k^3 =8*(8(k'')^3) =... jusqu'à k''_{n}£{0,1,8} donc a^2 = 4k'^2 = ... = (2^{2n})*k'{n} et si veut-on qu'il sera juste pour x^3 on doit appliquer une disjonction de cas sur k''_{n}£{0,1,8} pour trouver dans chaque fois une contradiction. Ainsi l'hypothèse est fausse. donc k pair et k'>l, on remarquera qu'on peut répéter cette phase n fois, et que x^3 =8k^3 =8*(8(k'')^3) =... jusqu'à k''_{n}£{0,1,8} donc a^2 = 4k'^2 = ... = (2^{2n})*k'{n} et si veut-on qu'il sera juste pour x^3 on doit appliquer une disjonction de cas sur k''_{n}£{0,1,8} pour trouver dans chaque fois une contradiction. Ainsi l'hypothèse est fausse. Cela me rappelle bien ce type de raisonnement:
http://fr.wikipedia.org/wiki/M%C3%A9thode_de_descente_infinie.
Je pense que ton raisonnement est bon. Merci. Pensez à résoudre le dernier problème que j'ai proposé. | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 11 Mar 2011, 18:29 Ven 11 Mar 2011, 18:29 | |
| - M.Marjani a écrit:
- D'autre coté,
=3a(a^2-b^2)\Rightarrow%20\exists%20m\in%20\mathbb{N*}\:%20/\:%20a(a^2-b^2)=4m) donc a,b ont la même parité. donc a,b ont la même parité. ??! | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 11 Mar 2011, 19:13 Ven 11 Mar 2011, 19:13 | |
| - M.Marjani a écrit:
- Problème 76 : *
Montrer que 798 devise y*x^{19}-x*y^{19} quelque soit x,y des entiers naturels . Je réponds: Tout ma solution repose sur le lemme suivant, appelé le petit théorème de Fermat: Soit a un entier relatif et p un nombre premier. Si p ne divise pas a, alors ) . Maintenant, je passe à notre exercice: On a d'un premier côté: 1,2,3,19 sont les diviseurs premiers de 798. Et encore: ) . Donc il faut démontrer que ) , ) , ) , et ) . Premièrement, démontrons qu'on a ) .==>(1) On distingue quatres cas, mai vu la symétriques des rôles entre x et y on se ramène à étudier les deux cas suivants seulement: *Cas premier: l'un des entier x et y est multiple de 19 ou bien tous les deux. Si 19 divise x, alors 19 divise ) . Si 19 divise y, alors 19 divise ) . *Cas second: aucun des entiers x et y n'est divisible par 19. Selon le lemme, on prends p=19, qui est bien premier. On a ) soit ) . De même ) . Ainsi \equiv0(19)) soit ) . Donc 19 divise 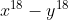 . Et par conséquent 19 divise ) . *Synthèse: On a \in\mathbb{N}):19/xy(x^{18}-y^{18})) . Deuxièmement, démontrons qu'on a ) .==>(2) On distingue quatres cas, mai vu la symétriques des rôles entre x et y on se ramène à étudier les deux cas suivants seulement: *Cas premier: l'un des entier x et y est multiple de 7 ou bien tous les deux. Si 7 divise x, alors 7 divise ) . Si 7 divise y, alors 7 divise ) . *Cas second: aucun des entiers x et y n'est divisible par 7. Selon le lemme, on prends p=7, qui est bien premier. On a ) soit ) . Donc ^3\equiv1(7)) soit ) . De même ) . Ainsi \equiv0(7)) soit ) . Donc 7 divise 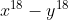 . Et par conséquent 7 divise ) . *Synthèse: On a \in\mathbb{N}):7/xy(x^{18}-y^{18})) . Troisièmement, démontrons qu'on a ) .==>(3) On distingue quatres cas, mai vu la symétriques des rôles entre x et y on se ramène à étudier les deux cas suivants seulement: *Cas premier: l'un des entier x et y est multiple de 3 ou bien tous les deux. Si 3 divise x, alors 3 divise ) . Si 3 divise y, alors 3 divise ) . *Cas second: aucun des entiers x et y n'est divisible par 3. Selon le lemme, on prends p=3, qui est bien premier. On a ) soit ) . Donc ^9\equiv1(3)) soit ) . De même ) . Ainsi \equiv0(3)) soit ) . Donc 3 divise 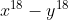 . Et par conséquent 3 divise ) . *Synthèse: On a \in\mathbb{N}):3/xy(x^{18}-y^{18})) . Quatrièmement, démontrons qu'on a ) .==>(4) On distingue quatres cas, mai vu la symétriques des rôles entre x et y on se ramène à étudier les deux cas suivants seulement: *Cas premier: l'un des entier x et y est multiple de 3 ou bien tous les deux. Si 2 divise x, alors 2 divise ) . Si 2 divise y, alors 2 divise ) . *Cas second: aucun des entiers x et y n'est divisible par 2. Selon le lemme, on prends p=2, qui est bien premier. On a ) soit ) . Donc ^{18}\equiv1(2)) soit ) . De même ) . Ainsi \equiv0(2)) soit ) . Donc 2 divise 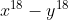 . Et par conséquent 2 divise ) . *Synthèse: On a \in\mathbb{N}):2/xy(x^{18}-y^{18})) . Finalement, et selon 1, 2, 3, et 4, on a \in\mathbb{N}):2\times3\times7\times19/xy(x^{18}-y^{18})) car ces entiers sont premiers entre eux. Donc \in\mathbb{N}):798/xy(x^{18}-y^{18})) . Ce qui met fin à la démonstration. P.S: J'ai préféré utilisé le lemme sur le quatrième cas même s'il est trivial. Vous remarquez aussi la ressemblance entre chaque étape, car je n'aipas voulu dire tout simplement "les autres cas se traitent de la même manière. J'attends une confirmation. | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 11 Mar 2011, 19:26 Ven 11 Mar 2011, 19:26 | |
| - nmo a écrit:
- M.Marjani a écrit:
- Problème 76 : *
Montrer que 798 devise y*x^{19}-x*y^{19} quelque soit x,y des entiers naturels . Je réponds:
Tout ma solution repose sur le lemme suivant, appelé le petit théorème de Fermat:
Soit a un entier relatif et p un nombre premier.
Si p ne divise pas a, alors ) . .
Maintenant, je passe à notre exercice:
On a d'un premier côté: 1,2,3,19 sont les diviseurs premiers de 798.
Et encore: ) . .
Donc il faut démontrer que ) , , ) , , ) , et , et ) . .
Premièrement, démontrons qu'on a ) .==>(1) .==>(1)
On distingue quatres cas, mai vu la symétriques des rôles entre x et y on se ramène à étudier les deux cas suivants seulement:
*Cas premier: l'un des entier x et y est multiple de 19 ou bien tous les deux.
Si 19 divise x, alors 19 divise ) . .
Si 19 divise y, alors 19 divise ) . .
*Cas second: aucun des entiers x et y n'est divisible par 19.
Selon le lemme, on prends p=19, qui est bien premier.
On a ) soit soit ) . .
De même ) . .
Ainsi \equiv0(19)) soit soit ) . .
Donc 19 divise 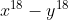 . .
Et par conséquent 19 divise ) . .
*Synthèse:
On a \in\mathbb{N}):19/xy(x^{18}-y^{18})) . .
Deuxièmement, démontrons qu'on a ) .==>(2) .==>(2)
On distingue quatres cas, mai vu la symétriques des rôles entre x et y on se ramène à étudier les deux cas suivants seulement:
*Cas premier: l'un des entier x et y est multiple de 7 ou bien tous les deux.
Si 7 divise x, alors 7 divise ) . .
Si 7 divise y, alors 7 divise ) . .
*Cas second: aucun des entiers x et y n'est divisible par 7.
Selon le lemme, on prends p=7, qui est bien premier.
On a ) soit soit ) . .
Donc ^3\equiv1(7)) soit soit ) . .
De même ) . .
Ainsi \equiv0(7)) soit soit ) . .
Donc 7 divise 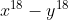 . .
Et par conséquent 7 divise ) . .
*Synthèse:
On a \in\mathbb{N}):7/xy(x^{18}-y^{18})) . .
Troisièmement, démontrons qu'on a ) .==>(3) .==>(3)
On distingue quatres cas, mai vu la symétriques des rôles entre x et y on se ramène à étudier les deux cas suivants seulement:
*Cas premier: l'un des entier x et y est multiple de 3 ou bien tous les deux.
Si 3 divise x, alors 3 divise ) . .
Si 3 divise y, alors 3 divise ) . .
*Cas second: aucun des entiers x et y n'est divisible par 3.
Selon le lemme, on prends p=3, qui est bien premier.
On a ) soit soit ) . .
Donc ^9\equiv1(3)) soit soit ) . .
De même ) . .
Ainsi \equiv0(3)) soit soit ) . .
Donc 3 divise 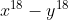 . .
Et par conséquent 3 divise ) . .
*Synthèse:
On a \in\mathbb{N}):3/xy(x^{18}-y^{18})) . .
Quatrièmement, démontrons qu'on a ) .==>(4) .==>(4)
On distingue quatres cas, mai vu la symétriques des rôles entre x et y on se ramène à étudier les deux cas suivants seulement:
*Cas premier: l'un des entier x et y est multiple de 3 ou bien tous les deux.
Si 2 divise x, alors 2 divise ) . .
Si 2 divise y, alors 2 divise ) . .
*Cas second: aucun des entiers x et y n'est divisible par 2.
Selon le lemme, on prends p=2, qui est bien premier.
On a ) soit soit ) . .
Donc ^{18}\equiv1(2)) soit soit ) . .
De même ) . .
Ainsi \equiv0(2)) soit soit ) . .
Donc 2 divise 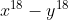 . .
Et par conséquent 2 divise ) . .
*Synthèse:
On a \in\mathbb{N}):2/xy(x^{18}-y^{18})) . .
Finalement, et selon 1, 2, 3, et 4, on a \in\mathbb{N}):2\times3\times7\times19/xy(x^{18}-y^{18})) car ces entiers sont premiers entre eux. car ces entiers sont premiers entre eux.
Donc \in\mathbb{N}):798/xy(x^{18}-y^{18})) . .
Ce qui met fin à la démonstration.
P.S: J'ai préféré utilisé le lemme sur le quatrième cas même s'il est trivial.
Vous remarquez aussi la ressemblance entre chaque étape, car je n'aipas voulu dire tout simplement "les autres cas se traitent de la même manière.
J'attends une confirmation. Très bien. A toi de poster un nouvel exercice ! | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 11 Mar 2011, 23:46 Ven 11 Mar 2011, 23:46 | |
| - Dijkschneier a écrit:
- M.Marjani a écrit:
- D'autre coté,
=3a(a^2-b^2)\Rightarrow%20\exists%20m\in%20\mathbb{N*}\:%20/\:%20a(a^2-b^2)=4m) donc a,b ont la même parité. donc a,b ont la même parité. ??! J'ai passé un peu vitement.. Elle se traite facilement mais longue. Il suffira ainsi de vérifier quand a est pair et b impair.
Tout qui se cache derrière ce problème c'est le fait de remarquer que x^3 = 2a(a² + 3b²) = (a - b)^3 + (a + b)^3
Et puis appliquer ce qu'à trouver Fermat. " L'équation x^n = y^n + z^n / n>2 n'a pas de solutions dans IN ".
Dernière édition par M.Marjani le Ven 11 Mar 2011, 23:56, édité 3 fois | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 11 Mar 2011, 23:51 Ven 11 Mar 2011, 23:51 | |
| - M.Marjani a écrit:
- Tout qui se cache derrière cet exercice, c'est le fait de remarquer que x^3 = 2a(a² + 3b²) = (a - b)^3 + (a + b)^3
Et puis appliquer ce qu'à trouver Fermat. " L'équation x^n = y^n + z^n / n>2 n'a pas de solutions dans IN ". Bien. Je te propose d'éditer ta première solution et de corriger. | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 12 Mar 2011, 14:30 Sam 12 Mar 2011, 14:30 | |
| Bon puisque personné n'a posté d'exercice, je me charge d'en poster un nouveau :
Problème 77 :
a et b et c sont des mesures des côtés d'un triangle, tel que a+b+c=2.
Montrez que : a²+b²+c²+2abc<2
| |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 12 Mar 2011, 17:12 Sam 12 Mar 2011, 17:12 | |
| Solution au problème 77 :
Comme a,b et c sont les côtés d'un triangle, alors on peut écrire a=x+y et cycliquement où x,y et z sont des réels positifs.
Puis on définit les quantités habituelles p = a+b+c, q=ab+ac+bc et r=abc
La condition de l'énoncé signifie p=1.
On doit prouver que ((p²-2q)+q)+(pq-r) < 1, ce qui est équivalent à r>0 étant donné la condition p=1, ce qui est trivial.
| |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 12 Mar 2011, 17:53 Sam 12 Mar 2011, 17:53 | |
| Et que chacun se sente libre de proposer de nouveaux problèmes. | |
|   | | boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 12 Mar 2011, 18:17 Sam 12 Mar 2011, 18:17 | |
| Salut
JE poste une autre solution d'exo 77
a>b+c d'ou 2a>2 a>1 de meme b>1 et c>1 d'ou (a-1)(1-b)(1-c)<0
a+b+c-ab-ac-bc+abc-1<0
1-ab-ac-bc+abc<0
d'une autre part (a+b+c)²=a²+b²+c²+2(ab+ac+bc)=4
ab+ac+bc=(4-a²-b²-c²)/2
l'inégalité devient 1-(4-a²-b²-c²)/2 + abc<0
2+a²+b²+c²-4+2abc<0
a²+b²+c²+2abc<2
AMICALEMENT . | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|   | | | | Préparations aux olympiades de première (2010-2011) |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
