|
| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants | |
| Auteur | Message |
|---|
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 25 Avr 2011, 00:05 Lun 25 Avr 2011, 00:05 | |
| | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 25 Avr 2011, 18:03 Lun 25 Avr 2011, 18:03 | |
| Les solutions proposées au problème 95 sont justes. Je propose un nouvel exercice: Problème 96:Soit ABCD un quadrilatère inscriptible. Les longueurs de ses côté sont a, b, c, et d et S sa surface. Infirmez ou confirmez les propostions suivantes: 1) 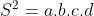 . 2)Si p est son demi-périmètre, .(p-b).(p-c).(p-d)) . 3)Si R est le rayon de son cercle inscrit, .(ca+bd).(ab+cd)}{16R^2}) . 4)Si 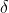 est un angle formé par l'intersection de ses diagonales, ) . Bonne chance. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 29 Avr 2011, 16:49 Ven 29 Avr 2011, 16:49 | |
| Voici un exercice de plus: Problème 97:Soit a et b deux réels tel que a<b. Déterminez toutes les applications f définie de [a,b] vers [a,b] et satisfait la relation -f(y)|\ge|x-y|) pour tous les réels x et y de l'ensemble [a,b]. Bonne chance. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 29 Avr 2011, 18:25 Ven 29 Avr 2011, 18:25 | |
|
Dernière édition par M.Marjani le Sam 30 Avr 2011, 11:08, édité 3 fois | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 29 Avr 2011, 18:36 Ven 29 Avr 2011, 18:36 | |
| - M.Marjani a écrit:
- Solution 97:
|f(x) - f(y)| = |x-y| : f(x)=f(y) ==> x=y donc f injective, et f(x)=y <==> |y - f(y)| = |x - y|
y-f(y) = x - y <==> x = 2y - f(y) Ou y-f(y) = y - x <==> f(y)=x , donc f est aussi surjective .
D'autre part, P(x+y , y) |f(x+y) + f(y)| = |x| , P(x, 0) : |f(x) + f(0)| = |x| , P(0) ==> f(0)=0, d’où on tire f(x) = x ou f(x) = -x .
|f(x) - f(y)| > |x-y| : On a |x - y| < |f(x) - f(y)| =< |f(x)| - |f(y)| et posant f(0)=c tel que c de [a,b].
P(x ,0): |x|+|c| < |f(x)| pour tout x de [a,b] (*) et P(y ,0): |y| < |c| - f(y)| => |f(x)| < |c|-|x| pour tout x de [a,b] (**)
De (*) et (**) on déduit que |x| + |c| < |f(x)| < |c| - |x| , mais |x| + |c| >= |c| - |x| d’où la contradiction ..
Réciproquement, f(x) = x et f(x) = -x répondent aux données .. D’où le résultat.
@nmo: Merci pour les théorèmes qui sont trop connus et importants dans un quadrilatère convexe .
Si ma solution est juste, et st si cela ne vous dérange pas, je poste un nouveau problème en attendant d'une démonstration élémentaire des résultats présentés . Qui te garantit que (x+y)€[a,b]. Pour ce qui est des problèmes de nmo, c'est vrai ce sont des propriétés dans un quadrilatère convexe, leur démonstration est du moins facile, elle consiste juste à de petites chasses d'angles et appliquer des théorèmes fondamentaux ( notamment la loi des sinus et Al-Kashi). Sinon le problème 97 reste toujours sans solution ... | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 30 Avr 2011, 11:05 Sam 30 Avr 2011, 11:05 | |
| - Mehdi.O a écrit:
- M.Marjani a écrit:
- Solution 97:
|f(x) - f(y)| = |x-y| : f(x)=f(y) ==> x=y donc f injective, et f(x)=y <==> |y - f(y)| = |x - y|
y-f(y) = x - y <==> x = 2y - f(y) Ou y-f(y) = y - x <==> f(y)=x , donc f est aussi surjective .
D'autre part, P(x+y , y) |f(x+y) + f(y)| = |x| , P(x, 0) : |f(x) + f(0)| = |x| , P(0) ==> f(0)=0, d’où on tire f(x) = x ou f(x) = -x .
|f(x) - f(y)| > |x-y| : On a |x - y| < |f(x) - f(y)| =< |f(x)| - |f(y)| et posant f(0)=c tel que c de [a,b].
P(x ,0): |x|+|c| < |f(x)| pour tout x de [a,b] (*) et P(y ,0): |y| < |c| - f(y)| => |f(x)| < |c|-|x| pour tout x de [a,b] (**)
De (*) et (**) on déduit que |x| + |c| < |f(x)| < |c| - |x| , mais |x| + |c| >= |c| - |x| d’où la contradiction ..
Réciproquement, f(x) = x et f(x) = -x répondent aux données .. D’où le résultat.
@nmo: Merci pour les théorèmes qui sont trop connus et importants dans un quadrilatère convexe .
Si ma solution est juste, et st si cela ne vous dérange pas, je poste un nouveau problème en attendant d'une démonstration élémentaire des résultats présentés .
Qui te garantit que (x+y)€[a,b].
Pour ce qui est des problèmes de nmo, c'est vrai ce sont des propriétés dans un quadrilatère convexe, leur démonstration est du moins facile, elle consiste juste à de petites chasses d'angles et appliquer des théorèmes fondamentaux ( notamment la loi des sinus et Al-Kashi).
Sinon le problème 97 reste toujours sans solution ... Certes, cette solution est erroné sans (x+y)€[a,b]. Ce problème mérite plus que 8 min de réflexion :d . Cet exercice se résous en utilisant les notions des limites .. Il semble que Mehdi.O s'en charge pour vous proposer une solution : ) | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 30 Avr 2011, 15:11 Sam 30 Avr 2011, 15:11 | |
| - M.Marjani a écrit:
- Mehdi.O a écrit:
- M.Marjani a écrit:
- Solution 97:
|f(x) - f(y)| = |x-y| : f(x)=f(y) ==> x=y donc f injective, et f(x)=y <==> |y - f(y)| = |x - y|
y-f(y) = x - y <==> x = 2y - f(y) Ou y-f(y) = y - x <==> f(y)=x , donc f est aussi surjective .
D'autre part, P(x+y , y) |f(x+y) + f(y)| = |x| , P(x, 0) : |f(x) + f(0)| = |x| , P(0) ==> f(0)=0, d’où on tire f(x) = x ou f(x) = -x .
|f(x) - f(y)| > |x-y| : On a |x - y| < |f(x) - f(y)| =< |f(x)| - |f(y)| et posant f(0)=c tel que c de [a,b].
P(x ,0): |x|+|c| < |f(x)| pour tout x de [a,b] (*) et P(y ,0): |y| < |c| - f(y)| => |f(x)| < |c|-|x| pour tout x de [a,b] (**)
De (*) et (**) on déduit que |x| + |c| < |f(x)| < |c| - |x| , mais |x| + |c| >= |c| - |x| d’où la contradiction ..
Réciproquement, f(x) = x et f(x) = -x répondent aux données .. D’où le résultat.
@nmo: Merci pour les théorèmes qui sont trop connus et importants dans un quadrilatère convexe .
Si ma solution est juste, et st si cela ne vous dérange pas, je poste un nouveau problème en attendant d'une démonstration élémentaire des résultats présentés .
Qui te garantit que (x+y)€[a,b].
Pour ce qui est des problèmes de nmo, c'est vrai ce sont des propriétés dans un quadrilatère convexe, leur démonstration est du moins facile, elle consiste juste à de petites chasses d'angles et appliquer des théorèmes fondamentaux ( notamment la loi des sinus et Al-Kashi).
Sinon le problème 97 reste toujours sans solution ...
Certes, cette solution est erroné sans (x+y)€[a,b]. Ce problème mérite plus que 8 min de réflexion :d .
Cet exercice se résous en utilisant les notions des limites ..
Il semble que Mehdi.O s'en charge pour vous proposer une solution : ) En fait, je n'ai même pas lu le problème quand j'ai posté mon message, j'ai juste jeté un oeil sur votre solution  . Actuellement, je suis débordé par des DS, donc je ne pourrais avoir du temps pour travailler ce problème qui me semble intéressant, je vous laisse la main  . | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 30 Avr 2011, 18:55 Sam 30 Avr 2011, 18:55 | |
| - Mehdi.O a écrit:
- Pour ce qui est des problèmes de nmo, c'est vrai ce sont des propriétés dans un quadrilatère convexe, leur démonstration est du moins facile, elle consiste juste à de petites chasses d'angles et appliquer des théorèmes fondamentaux ( notamment la loi des sinus et Al-Kashi).
Voici un lien qui peut aider à trouver les démonstrations des trois dernières propositions: http://fr.wikipedia.org/wiki/Quadrilat%C3%A8re_inscriptible. Cependant, est ce que la première est juste? Franchement, c'est une propriété que j'ai connu dans un site, et j'ai bien aimé avoir une preuve. Et pour le problème 97, une chose est correcte, voire certaine: il existe deux fonctions qui répondent au problème. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 07 Mai 2011, 20:02 Sam 07 Mai 2011, 20:02 | |
| - nmo a écrit:
- Voici un exercice de plus:
Problème 97:
Soit a et b deux réels tel que a<b.
Déterminez toutes les applications f définie de [a,b] vers [a,b] et satisfait la relation -f(y)|\ge|x-y|) pour tous les réels x et y de l'ensemble [a,b]. pour tous les réels x et y de l'ensemble [a,b].
Bonne chance. Il paraît que personne n'a trouvé la solution, je propose la mienne: Soit g une application définie par g(x)=a+b-f(x). Soient x et y deux réels de l'ensemble [a,b]. Démontrons que g est définie de [a,b] vers [a,b], on a: \le b&\Leftrightarrow -b\le-f(x)\le-a\\&\Leftrightarrow a+b-b\le a+b-f(x)\le a+b-b\\&\Leftrightarrow a\le g(x)\le b\end{align*}) . Donc g est définie de [a,b] vers [a,b]. Maintenant, soit f une solution éventuelle du problème, on a: -f(y)|\ge|x-y|&\Leftrightarrow |a+b-f(y)-(a+b-f(x))|\ge|x-y|\\&\Leftrightarrow |g(y)-g(x)|\ge|x-y|\\&\Leftrightarrow |g(x)-g(y)|\ge|x-y|\end{align*}) . Il s'ensuit que g est une solution pour l'équation fonctionnelle. On suppose maintenant, sans perdre de généralité que \ge f(a)) . On prend x=a et y=b, il vient dans l'équation fonctionnelle que -f(b)|\ge|a-b|) . Soit -f(a)\ge b-a) .==>(1) Et d'autre part, on a: \le b\text{ et }a\le f(a)\le b&\Rightarrow a\le f(b)\le b\text{ et }-b\le -f(a)\le-a\\&\Rightarrow a-b\le f(b)-f(a)\le b-a\\&\Leftrightarrow -(b-a)\le f(b)-f(a)\le b-a\\&\Leftrightarrow f(b)-f(a)\le |b-a|\\&\Leftrightarrow f(b)-f(a)\le b-a\end{align*}) . Et en vertu de 1, il s'ensuit que -f(a)=b-a) . Soit -a+b-f(b)=0) .==>(2) Et d'autre part, on a aussi: \le b\text{ et }a\le f(b)\le b&\Rightarrow 0\le f(a)-a\text{ et }0\le b-f(b)\end{align*}) . Revenons à 2, il vient: -a=0) et -b=0) . Donc =a) et =b) . On prend y=a, il vient dans l'équation fonctionnelle que: -f(a)|\ge|x-a|&\Leftrightarrow |f(x)-a|\ge|x-a|\\&\Leftrightarrow f(x)-a\ge x-a\\&\Leftrightarrow f(x)\ge x\end{align*}) . On prend y=b, il vient dans l'équation fonctionnelle que: -f(b)|\ge|x-b|&\Leftrightarrow |f(x)-b|\ge|x-b|\\&\Leftrightarrow b-f(x)\ge b-x\\&\Leftrightarrow x\ge f(x)\end{align*}) . Les deux dernières résultats, affirment que =x) , pour tout x de [a,b]. Inversement, soit f la fonction définie par: f(x)=x. Cette application vérifie bel et bien l'équation fonctionnelle. Ainsi l'identité sur [a,b] est solution à l'équation fonctionnelle. Et aussi la fonction g définie par =a+b-f(x)) , soit =a+b-x) , est solution à l'équation fonctionnelle. On en déduit que le problème admet deux solutions, qui sont l'identité sur [a,b] et 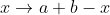 . Sauf erreur. En attente d'une confirmation. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 07 Mai 2011, 22:45 Sam 07 Mai 2011, 22:45 | |
| - nmo a écrit:
- nmo a écrit:
- Voici un exercice de plus:
Problème 97:
Soit a et b deux réels tel que a<b.
Déterminez toutes les applications f définie de [a,b] vers [a,b] et satisfait la relation -f(y)|\ge|x-y|) pour tous les réels x et y de l'ensemble [a,b]. pour tous les réels x et y de l'ensemble [a,b].
Bonne chance. Il paraît que personne n'a trouvé la solution, je propose la mienne:
Soit g une application définie par g(x)=a+b-f(x).
Soient x et y deux réels de l'ensemble [a,b].
Démontrons que g est définie de [a,b] vers [a,b], on a:
\le b&\Leftrightarrow -b\le-f(x)\le-a\\&\Leftrightarrow a+b-b\le a+b-f(x)\le a+b-b\\&\Leftrightarrow a\le g(x)\le b\end{align*}) . .
Donc g est définie de [a,b] vers [a,b].
Maintenant, soit f une solution éventuelle du problème, on a:
-f(y)|\ge|x-y|&\Leftrightarrow |a+b-f(y)-(a+b-f(x))|\ge|x-y|\\&\Leftrightarrow |g(y)-g(x)|\ge|x-y|\\&\Leftrightarrow |g(x)-g(y)|\ge|x-y|\end{align*}) . .
Il s'ensuit que g est une solution pour l'équation fonctionnelle.
On suppose maintenant, sans perdre de généralité que \ge f(a)) . .
On prend x=a et y=b, il vient dans l'équation fonctionnelle que -f(b)|\ge|a-b|) . .
Soit -f(a)\ge b-a) .==>(1) .==>(1)
Et d'autre part, on a:
\le b\text{ et }a\le f(a)\le b&\Rightarrow a\le f(b)\le b\text{ et }-b\le -f(a)\le-a\\&\Rightarrow a-b\le f(b)-f(a)\le b-a\\&\Leftrightarrow -(b-a)\le f(b)-f(a)\le b-a\\&\Leftrightarrow f(b)-f(a)\le |b-a|\\&\Leftrightarrow f(b)-f(a)\le b-a\end{align*}) . .
Et en vertu de 1, il s'ensuit que -f(a)=b-a) . .
Soit -a+b-f(b)=0) .==>(2) .==>(2)
Et d'autre part, on a aussi:
\le b\text{ et }a\le f(b)\le b&\Rightarrow 0\le f(a)-a\text{ et }0\le b-f(b)\end{align*}) . .
Revenons à 2, il vient: -a=0) et et -b=0) . .
Donc =a) et et =b) . .
On prend y=a, il vient dans l'équation fonctionnelle que:
-f(a)|\ge|x-a|&\Leftrightarrow |f(x)-a|\ge|x-a|\\&\Leftrightarrow f(x)-a\ge x-a\\&\Leftrightarrow f(x)\ge x\end{align*}) . .
On prend y=b, il vient dans l'équation fonctionnelle que:
-f(b)|\ge|x-b|&\Leftrightarrow |f(x)-b|\ge|x-b|\\&\Leftrightarrow b-f(x)\ge b-x\\&\Leftrightarrow x\ge f(x)\end{align*}) . .
Les deux dernières résultats, affirment que =x) , pour tout x de [a,b]. , pour tout x de [a,b].
Inversement, soit f la fonction définie par: f(x)=x.
Cette application vérifie bel et bien l'équation fonctionnelle.
Ainsi l'identité sur [a,b] est solution à l'équation fonctionnelle.
Et aussi la fonction g définie par =a+b-f(x)) , soit , soit =a+b-x) , est solution à l'équation fonctionnelle. , est solution à l'équation fonctionnelle.
On en déduit que le problème admet deux solutions, qui sont l'identité sur [a,b] et 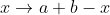 . .
Sauf erreur.
En attente d'une confirmation. Oui. Trés bonne solution. Il te reste une qui vérifie l'équation fonctionelle et compliqué, f(x) = -x . | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 07 Mai 2011, 23:04 Sam 07 Mai 2011, 23:04 | |
| f(x)=-x n'est pas une solution.
Car sinon x€[a,b]=>f(x)€[-b,-a] Contradiction | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 08 Mai 2011, 00:30 Dim 08 Mai 2011, 00:30 | |
| - Mehdi.O a écrit:
- f(x)=-x n'est pas une solution.
Car sinon x€[a,b]=>f(x)€[-b,-a] Contradiction Quel est le probléme dans ce que tu dis ? " x€[a,b] => f(x)€[-b,-a] " est forcement juste si -b=a mon cher . T'as commis une faute . Si -b=a nous obtiendrons b un réel positive, et c'est ainsi que l'intervalle ]-b, b[ devrait être discuté sauf erreur . | |
|   | | yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 08 Mai 2011, 10:19 Dim 08 Mai 2011, 10:19 | |
| Je crois que nmo la deja prouve, tant qu'il a prouver que a+b-x est une solution a l'equation. on peut prendre a=-b comme tu as dit et deduire la fonction x-->-x.
sauf erreur
| |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 08 Mai 2011, 10:33 Dim 08 Mai 2011, 10:33 | |
| Non, c'est faux. a et b sont supposés être fixes, donc on ne peut pas leur donner des valeurs! | |
|   | | yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 08 Mai 2011, 11:14 Dim 08 Mai 2011, 11:14 | |
|
Dernière édition par yasserito le Dim 08 Mai 2011, 13:23, édité 1 fois | |
|   | | boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 08 Mai 2011, 11:45 Dim 08 Mai 2011, 11:45 | |
| c'est un peu hors sujet mais j'ai une question pour ceux qui ont passé les olympiades du TC l’année dernière , cb de phase vous avez passé ?? | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 08 Mai 2011, 11:54 Dim 08 Mai 2011, 11:54 | |
| En ce qui me concerne, j'en ai passé trois si on peut dire, car la première se fait au sein de l'établissement pour choisir les élèves aptes de se présenter aux olympiades régionaux.
En outre, cela ne sert absolument à rien vu que d'emblée on ne prend pas en considération le passage en tronc commun pour participer aux olympiades de première.
Il me semble que le même scénario se répète cette année, vu que ces six épreuves qu'on a passé ne servent absolument à rien. On en choisira d'autres à nouveau en Terminale.
Bref, c'est le Maroc ! | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 08 Mai 2011, 13:47 Dim 08 Mai 2011, 13:47 | |
| - nmo a écrit:
- Mehdi.O a écrit:
- Pour ce qui est des problèmes de nmo, c'est vrai ce sont des propriétés dans un quadrilatère convexe, leur démonstration est du moins facile, elle consiste juste à de petites chasses d'angles et appliquer des théorèmes fondamentaux ( notamment la loi des sinus et Al-Kashi).
Voici un lien qui peut aider à trouver les démonstrations des trois dernières propositions:
http://fr.wikipedia.org/wiki/Quadrilat%C3%A8re_inscriptible.
Cependant, est ce que la première est juste?
Franchement, c'est une propriété que j'ai connu dans un site, et j'ai bien aimé avoir une preuve. Je démontre la fausseté de la formule S²=a.b.c.d . Prenons par exemple un trapèze isocèle ABCD de bases [AB] et [CD]. Le quadrilatère ABCD est inscriptible par définition. Choisissons AB=2, BC=3, CD=5, et DA=3. Selon la formule précédante, on a S²=3*5*3*2=90.==>(1) Or, on sait que \times h}{2}) tel que h est la hauteur de ce trapèze. On sait que: ^2+h^2=BC^2) . Donc ^2=9-(\frac{3}{2})^2=9-\frac{9}{4}=\frac{27}{4}) . Donc 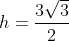 . On écrit: \times h}{2}=\frac{(2+5)\times\frac{3\sqrt{3}}{2}}{2}=\frac{7\times 3\sqrt{3}}{2\times2}=\frac{21\sqrt{3}}{4}) . Et puis: ^2) .==>(2) On voit largement une contradiction entre 1 et 2. D'où la fausseté de la formule. Sauf erreur. - Mehdi.O a écrit:
- Il me semble que le même scénario se répète cette année, vu que ces six épreuves qu'on a passé ne servent absolument à rien. On en choisira d'autres à nouveau en Terminale.
Non, je te fait part de ce que je sait: les notes de ces six tests sont pris en considération car: -Si par exemple un élève a pu se califier seul dans un établissement, alors cet établissement est qualifié l'année prochaine et 10 élèves vont pouvoir participer avec l'élève qualifié de première, c'est le cas de cette année. -Par contre, si personne n'a atteint le sixième test, l'établissement est disqualifié et personne ne participera l'année prochaine de cet établissement. | |
|   | | Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 08 Mai 2011, 14:19 Dim 08 Mai 2011, 14:19 | |
| - nmo a écrit:
- nmo a écrit:
- Mehdi.O a écrit:
- Pour ce qui est des problèmes de nmo, c'est vrai ce sont des propriétés dans un quadrilatère convexe, leur démonstration est du moins facile, elle consiste juste à de petites chasses d'angles et appliquer des théorèmes fondamentaux ( notamment la loi des sinus et Al-Kashi).
Voici un lien qui peut aider à trouver les démonstrations des trois dernières propositions:
http://fr.wikipedia.org/wiki/Quadrilat%C3%A8re_inscriptible.
Cependant, est ce que la première est juste?
Franchement, c'est une propriété que j'ai connu dans un site, et j'ai bien aimé avoir une preuve. Je démontre la fausseté de la formule S²=a.b.c.d .
Prenons par exemple un trapèze isocèle ABCD de bases [AB] et [CD].
Le quadrilatère ABCD est inscriptible par définition.
Choisissons AB=2, BC=3, CD=5, et DA=3.
Selon la formule précédante, on a S²=3*5*3*2=90.==>(1)
Or, on sait que \times h}{2}) tel que h est la hauteur de ce trapèze. tel que h est la hauteur de ce trapèze.
On sait que: ^2+h^2=BC^2) . .
Donc ^2=9-(\frac{3}{2})^2=9-\frac{9}{4}=\frac{27}{4}) . .
Donc 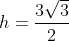 . .
On écrit: \times h}{2}=\frac{(2+5)\times\frac{3\sqrt{3}}{2}}{2}=\frac{7\times 3\sqrt{3}}{2\times2}=\frac{21\sqrt{3}}{4}) . .
Et puis: ^2) .==>(2) .==>(2)
On voit largement une contradiction entre 1 et 2.
D'où la fausseté de la formule.
Sauf erreur.
- Mehdi.O a écrit:
- Il me semble que le même scénario se répète cette année, vu que ces six épreuves qu'on a passé ne servent absolument à rien. On en choisira d'autres à nouveau en Terminale.
Non, je te fait part de ce que je sait: les notes de ces six tests sont pris en considération car:
-Si par exemple un élève a pu se califier seul dans un établissement, alors cet établissement est qualifié l'année prochaine et 10 élèves vont pouvoir participer avec l'élève qualifié de première, c'est le cas de cette année.
-Par contre, si personne n'a atteint le sixième test, l'établissement est disqualifié et personne ne participera l'année prochaine de cet établissement. On ne peut pas prendre de tels valeurs, en outre qui garantit qu'un tel quadrilatère existe? Pour clarifier, c'est comme si on donnait un triangle ds valeurs AB=1 et AC=2 et BC=4 c'est complètent paradoxal, vu que l'inégalité triangulaire n'a pas lieu. J'espère que tu as compris ma remarque. | |
|   | | boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 08 Mai 2011, 16:11 Dim 08 Mai 2011, 16:11 | |
| Merci pour les infos Mr Mehdi  | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 10 Mai 2011, 01:18 Mar 10 Mai 2011, 01:18 | |
| Merci pour les informations nmo !
Et pertinente remarque Mehdi . L'existence d'un tel quadrilatére est trés importante dans ce cas.
Mais l'idée générale reste de prouver sa fauseté en un contre exemple.
Probléme 98 :
Résoudre en |N l'équation suivante : 2^p + 3^p = a^n quand n >= 2 et p un nombre premiér. | |
|   | | Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 10 Mai 2011, 18:57 Mar 10 Mai 2011, 18:57 | |
| - M.Marjani a écrit:
Probléme 98 :
Résoudre en |N l'équation suivante : 2^p + 3^p = a^n quand n >= 2 et p un nombre premiér. - Spoiler:
V_5(2^p+3^p)=V_5(a^n) = V_(5)(2+3)+V_5(p)=1+V_5(p)>0 ==> 5|a (car 5 |2+3 et dapres LTE)
donc V_5(a^n)=n =V_5(2+3)+V_5(p)
si p ne divise pas 5 donc n=V_5(2+3)=1
si p=5 a^n=2^5+3^5 ==> n=1
donc toujours pas de solutions .
sauf erreur ! | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 10 Mai 2011, 21:53 Mar 10 Mai 2011, 21:53 | |
| Joli Sporovitch :d 2éme Solution au probléme 98 :- Spoiler:
C'est à vous .
Dernière édition par M.Marjani le Mer 11 Mai 2011, 20:13, édité 4 fois | |
|   | | Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 11 Mai 2011, 13:37 Mer 11 Mai 2011, 13:37 | |
| - M.Marjani a écrit:
- Joli Sporovitch :d
 au lieu de 0[2] . au lieu de 0[2] .
C'est à vous . j'ai pa tres bien lu ce que t'as écrit mais ya-il une différence entre 0[2] et 2[2]  Probleme 99 : résoudre dans Z l'équation : x^3+x²+x=y²+y | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 12 Mai 2011, 01:22 Jeu 12 Mai 2011, 01:22 | |
| - Sporovitch a écrit:
- M.Marjani a écrit:
- Joli Sporovitch :d
 au lieu de 0[2] . au lieu de 0[2] .
C'est à vous . j'ai pa tres bien lu ce que t'as écrit mais ya-il une différence entre 0[2] et 2[2]  Oui oui, j'ai voullu écrire encore 2[p] au lieu de 2[2] , c'est normal aprés l'application de Fermat :p bonne remarque et j'ai réctifié . - Citation :
- Probleme 99 :
résoudre dans Z l'équation :
x^3+x²+x=y²+y
Si 0=y on aura le couple (0 ,0) solution vérifiant l'équation. Aussi x^3 + x² + x = y² + y <==> (y-x)(x+y+1) = x^3 .
Donc y - x | x^3 et x+y+1 | x^3 et car x|x^3 que y|x^3 et y + 1|x^3, et du fait que PGCD(y, y+1) = 1 alors |y|=1 .
Ou bien -2 = y qui ne vérifie point l'équation. Et ce sera cette fois (0, -1) notre deuxiéme et dernier couple. CQFD?
| |
|   | | Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|   | | | | Préparations aux olympiades de première (2010-2011) |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
