Préparations aux olympiades de première (2010-2011)

M.Marjani a écrit:

Sporovitch a écrit:

M.Marjani a écrit:

Joli Sporovitch :d

au lieu de 0[2] .

C'est à vous .

j'ai pa tres bien lu ce que t'as écrit mais ya-il une différence entre 0[2] et 2[2]

Oui oui, j'ai voullu écrire encore 2[p] au lieu de 2[2] , c'est normal aprés l'application de Fermat :p bonne remarque et j'ai réctifié .

Citation :

Probleme 99 :
résoudre dans Z l'équation :
x^3+x²+x=y²+y

Si 0=y on aura le couple (0 ,0) solution vérifiant l'équation. Aussi x^3 + x² + x = y² + y <==> (y-x)(x+y+1) = x^3 .
Donc y - x | x^3 et x+y+1 | x^3 et car x|x^3 que y|x^3 et y + 1|x^3, et du fait que PGCD(y, y+1) = 1 alors |y|=1 .
Ou bien -2 = y qui ne vérifie point l'équation. Et ce sera cette fois (0, -1) notre deuxiéme et dernier couple. CQFD?

C'est faux le fait que PGCD(y,y+1)=1 implique tout simplement que 1|x^3 ce qui est clairement vrai.
En outre conclure que |y|=1 est faux!

Sporovitch a écrit:

Probleme 99 :
résoudre dans Z l'équation :
x^3+x²+x=y²+y

M.Marjani a écrit:

Si 0=y on aura le couple (0 ,0) solution vérifiant l'équation. Aussi x^3 + x² + x = y² + y <==> (y-x)(x+y+1) = x^3 .
Donc y - x | x^3 et x+y+1 | x^3 et car x|x^3 que y|x^3 et y+1|x^3, et du fait que PGCD(y, y+1) = 1 alors |y|=1 .
Ou bien -2 = y qui ne vérifie point l'équation. Et ce sera cette fois (0, -1) notre deuxiéme et dernier couple. CQFD?

Mehdi.O a écrit:

C'est faux le fait que PGCD(y,y+1)=1 implique tout simplement que 1|x^3 ce qui est clairement vrai.
En outre conclure que |y|=1 est faux!

|y|=1 ==> y=1 ou -1=y n'est ce pas ? Donc |y|=1 vient de -1=y qu'on ne peut pas dire qu'elle vérifie y+1|x^3 [la division par 0 est impossible] et le couple (0,0) est déjà discuté, c'est pourquoi je ne l'ai pas prise en considération dans la deuxiéme ligne). Donc 1=x qui est clairement impossible vu que y(y+1) = 3 et que y(y+1) est pair.
Cela répond à ta question ?

On n'a pas |y|=1 ...
Révise ta solution.

Mehdi.O a écrit:

On n'a pas |y|=1 ...
Révise ta solution.

Je sais qu'on l'a pas, et je pense que tous le sait Tous ce qui reste c'est de lire attentivement mon dernier message. Il vaut mieux voir |y|=1 comme si -1=y et elle ne vient plus au hasard.

Probléme 100 :

Si c'étaient a,b,c des réels strictement positives et qui vérifient abc =< 1 alors montrer que:

a/b + b/c + c/a >= a + b + c

M.Marjani a écrit:

Mehdi.O a écrit:

On n'a pas |y|=1 ...
Révise ta solution.

Je sais qu'on l'a pas, et je pense que tous le sait Tous ce qui reste c'est de lire attentivement mon dernier message. Il vaut mieux voir |y|=1 comme si -1=y et elle ne vient plus au hasard.

Probléme 100 :

Si c'étaient a,b,c des réels qui vérifient abc =< 1 alors montrer que:

a/b + b/c + c/a >= a + b + c

L'énoncé est ou bien faux,ou bien incomplet: prendre a=2;b=(-1/4);c=(1/2)

W.Elluizi a écrit:

M.Marjani a écrit:

Mehdi.O a écrit:

On n'a pas |y|=1 ...
Révise ta solution.

Je sais qu'on l'a pas, et je pense que tous le sait Tous ce qui reste c'est de lire attentivement mon dernier message. Il vaut mieux voir |y|=1 comme si -1=y et elle ne vient plus au hasard.

Probléme 100 :

Si c'étaient a,b,c des réels positives qui vérifient abc =< 1 alors montrer que:

a/b + b/c + c/a >= a + b + c

L'énoncé est ou bien faux,ou bien incomplet: prendre a=2;b=(-1/4);c=(1/2)

Oui . C'est édité ! Normalement les trois variables doivent être strictement positives .
Je m'en excuse pour l'erreur, qui est due à l'origine oû se trouve l'exercice . Et Merci pour votre attention .

M.Marjani a écrit:

Citation :

Probleme 99 :
résoudre dans Z l'équation :
x^3+x²+x=y²+y

Si 0=y on aura le couple (0 ,0) solution vérifiant l'équation. Aussi x^3 + x² + x = y² + y <==> (y-x)(x+y+1) = x^3 .
Donc y - x | x^3 et x+y+1 | x^3 et car x|x^3 que y|x^3 et y + 1|x^3, et du fait que PGCD(y, y+1) = 1 alors |y|=1 .
Ou bien -2 = y qui ne vérifie point l'équation. Et ce sera cette fois (0, -1) notre deuxiéme et dernier couple. CQFD?

Ce qui est en rouge est faux, car du fait que y-x divise x^3 on ne peut pas affirmer que y divise x^3.
Tu confonds avec la réciproque qui est vrai: si a divise a.k+b alors a divise b.
A ce que je vois, il n'existe que tes deux solutions (0,0) et (0,-1) qui doivent être prouvés plus rigoureusement.

Sporovitch a écrit:

M.Marjani a écrit:

Joli Sporovitch :d

au lieu de 0[2] .

C'est à vous .

j'ai pa tres bien lu ce que t'as écrit mais ya-il une différence entre 0[2] et 2[2]
Probleme 99 :
résoudre dans Z l'équation :
x^3+x²+x=y²+y

Solution du problème :
Je ne pourrais surement pas donner de solution plus élégante que celle déjà présenter , mais bon j'essai quand même :
le cas de 0 est clair .si x et y différent de 0
on a x|y ou x|y+1
si x|y on écrit y=kx l'équation devient donc :
x^3+x²+x=k²x²+kx <==> x²+x+1=k²x+k ==> x|k-1 on pose k=k'x+1 <==> x²+x+1=(k'x+1)²x+k'x+1 <==> x+1=(k'x+1)²+k' <==>
x=k'²x²+2k'x + k' ==> x|k' et k'|x donc x=|k'| .
x=x^(4)+2x^2+x ou x=x^(4)-2x^2 -x
x^4+2x^2=0 | x^3-2x-2=0
x=0 absurde | x(x²-2)=2 absurde

si x|(y+1) y=kx-1
x^3+x²+x=(kx-1)²+kx-1 <==> x²+x+1= k²x-k ==> x|k+1 k=k'x-1 <==> x²+x+1=(k'x-1)²x-k'x+1 <==> x+1=(k'x-1)²-k'<==>

x+1=k'²x²-2k'x+1-k' <==> x= k'²x²-2k'x-k' ==> x=|k'|
x=x^4-2x^2-x ou x=x^4+2x^2+x et on fait comme pour l'autre . S=(0,0);(0,-1)
SAUF ERREUR ( solution un peu longue je trouve )

darkpseudo a écrit:

Sporovitch a écrit:

Probleme 99 :
résoudre dans Z l'équation :
x^3+x²+x=y²+y

Solution du problème :
Je ne pourrais surement pas donner de solution plus élégante que celle déjà présenter , mais bon j'essai quand même :
le cas de 0 est clair .si x et y différent de 0
on a x|y ou x|y+1
si x|y on écrit y=kx l'équation devient donc :
x^3+x²+x=k²x²+kx <==> x²+x+1=k²x+k ==> x|k-1 on pose k=k'x+1 <==> x²+x+1=(k'x+1)²x+k'x+1 <==> x+1=(k'x+1)²+k' <==>
x=k'²x²+2k'x + k' ==> x|k' et k'|x donc x=|k'| .
x=x^(4)+2x^2+x ou x=x^(4)-2x^2 -x
x^4+2x^2=0 | x^3-2x-2=0
x=0 absurde | x(x²-2)=2 absurde
si x|(y+1) y=kx-1
x^3+x²+x=(kx-1)²+kx-1 <==> x²+x+1= k²x-k ==> x|k+1 k=k'x-1 <==> x²+x+1=(k'x-1)²x-k'x+1 <==> x+1=(k'x-1)²-k'<==> x+1=k'²x²-2k'x+1-k' <==> x= k'²x²-2k'x-k' ==> x=|k'|
x=x^4-2x^2-x ou x=x^4+2x^2+x et on fait comme pour l'autre . S=(0,0);(0,-1)
SAUF ERREUR ( solution un peu longue je trouve )

Cette solution me plaît largement.
Très bien darkpseudo.

Celui qui résout un exercice, qu'il poste un problème.

PROBLEME 101 :

Résoudre dans Q^3 :
x^3+2y^3+4z^3=6xyz

M.Marjani a écrit:

Si 0=y on aura le couple (0 ,0) solution vérifiant l'équation. Aussi x^3 + x² + x = y² + y <==> (y-x)(x+y+1) = x^3 .
Donc y - x | x^3 et x+y+1 | x^3 et car x|x^3 que y|x^3 et y + 1|x^3, et du fait que PGCD(y, y+1) = 1 alors |y|=1 .
Ou bien -2 = y qui ne vérifie point l'équation. Et ce sera cette fois (0, -1) notre deuxiéme et dernier couple. CQFD?

Une révolution dans le Monde d'arithémtiques

ELHANSIFIDANCIWLEXCELENCI a écrit:

je crois que Mehdi.A a raison mais je ne suis pas sur
merci de confirmer ma theorie

Merci de joindre une preuve complète et claire à ce que tu viens de dire !

Mr. ELHANSIFIDANCIWLEXCELENCI ! Veuillez jetez un coup d'oeil sur les deux liens suivants qui montrent la différence entre THEORIE et THEOREME:
http://fr.wikipedia.org/wiki/Th%C3%A9orie
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me
C'est quoi cette histoire de règle graduée???

PS: C'est mon 100e message!!!

T'as entendu ELHANSIFIDANCIWLEXCELENCI Olalaalaala faut faire la différence , XD et puis joli l'effort fourni sur l'orthographe , sinon j'éspère quand te reverra bientot

ELHANSIFIDANCIWLEXCELENCI a écrit:

je n'arriv po a metre au point une preuv clère neanmoin je crois que la theorie de la regle graduee pourra nous etre d'un interet (2min)
nous attendons bien sur la confirmation de nos leaders (monsieur marjani, metaich, spitikha, etc)

Je ne pense pas que la théorie de la régle graduée peut t'aider vu que les transformations géometriques sont pas triviales dans ce cas !
Or Penser à la théorie de la vie courante me semble plus efficace meme si c'est peu difficil je l'ai résolu hier (45 min)

nmo a écrit:

M.Marjani a écrit:

Citation :

Probleme 99 :
résoudre dans Z l'équation :
x^3+x²+x=y²+y

Si 0=y on aura le couple (0 ,0) solution vérifiant l'équation. Aussi x^3 + x² + x = y² + y <==> (y-x)(x+y+1) = x^3 .
Donc y - x | x^3 et x+y+1 | x^3 et car x|x^3 que y|x^3 et y + 1|x^3, et du fait que PGCD(y, y+1) = 1 alors |y|=1 .
Ou bien -2 = y qui ne vérifie point l'équation. Et ce sera cette fois (0, -1) notre deuxiéme et dernier couple. CQFD?

Ce qui est en rouge est faux, car du fait que y-x divise x^3 on ne peut pas affirmer que y divise x^3.
Tu confonds avec la réciproque qui est vrai: si a divise a.k+b alors a divise b.
A ce que je vois, il n'existe que tes deux solutions (0,0) et (0,-1) qui doivent être prouvés plus rigoureusement.

Oups ! trés grave ! Je m'en excuse vraiment une deuxiéme fois .. oui je l'ai confondu avec y-x|x^3 et y-x|y^3 Il n'y a plus de maths à minuit :d


Et bien joué Othmane

M.Marjani a écrit:

Probléme 100 :
Si c'étaient a,b,c des réels strictement positives et qui vérifient abc =< 1 alors montrer que:
a/b + b/c + c/a >= a + b + c

On a selon l'inégalité arithmético-géométrique: .
Soit .
Et on a d'autre part, selon l'énoncé du problème:
.
Soit en résumé .==>(1)
Et par analogie, on se ramène à .==>(2)
Et à .==>(3)
En sommant 1, 2, et 3 on trouve: Soit en résumé .
Donc .
Soit en résumé .
CQFD.

darkpseudo a écrit:

Résoudre dans Q^3 :
x^3+2y^3+4z^3=6xyz

Ton problème est numéroté 101.
Merci de rectifier.
P.S: c'est le problème courant.

nmo a écrit:

M.Marjani a écrit:

Probléme 100 :
Si c'étaient a,b,c des réels strictement positives et qui vérifient abc =< 1 alors montrer que:
a/b + b/c + c/a >= a + b + c

On a selon l'inégalité arithmético-géométrique: .
Soit .
Et on a d'autre part, selon l'énoncé du problème:
.
Soit en résumé .==>(1)
Et par analogie, on se ramène à .==>(2)
Et à .==>(3)
En sommant 1, 2, et 3 on trouve: Soit en résumé .
Donc .
Soit en résumé .
CQFD.

Trés jolie. Bien.

pr ce qui concerne ; j'ai enfin trouvé une autre solution qui est vraiment elegante en utilisant
the socks theoreme qui est un peut dificile aà comprendre mais je pense que notre savant marjani peut vous expliquez cette complex theoreme (qui est en realité une teorie)

Salut tout le monde je voudrais rejoindre les préparations aux olympiades . Pourriez vous m'expliquer comment je peux poster les réponses en mode mathématique.

darkpseudo a écrit:

PROBLEME 101 :
Résoudre dans Q^3 :
x^3+2y^3+4z^3=6xyz

Je réponds, même si je ne suis pas certains de ma solution:
Je vais me sevir de l'identité remarquable: .
Si on a .
Alors .
Et par conséquent, ou bien , ou bien .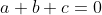
Le deuxième cas est facile, on considère donc le cas où .
Donc , , et .
Ainsi 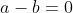, 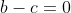, et .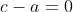
Soit 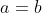, 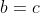, et .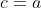
Et finalement .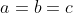
Je reviens à notre problème:
On prends 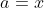, , et .
Ainsi l'équation proposée entraine ou bien ou bien .
Cas premier: .
Si y est différent de 0, alors .
Ce qui est absurde, car .
Il en résulte que y=0, et par conséquent x=z=0.
Cas second: .
Je démontre d'abord l'équivalence suivante: .
Soit r un nombre irrationnel:
-Supposons que , et démontrons que k=0.
On a .
Il existe daonc un nombre rationnel q tel que .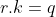
Supposons par l'absurde que k est différent de zéro.
Ainsi .
Et par conséquent r est un nombre rationnel, ce qui est absurde.
On en conclut que k=0.
-L'autre implication est tout à fait triviale.
Il en résulte que .
On a .
Donc .
Soit .
On sait d'ores et déjà que est un nombre rationnel.
Et selon l'équivalence que je viens de démontrer, il vient que .
Soit .
Si z est différent de zéro, on aura une contradiction pareille à la première.
Donc z=0, et cela conduit à y=0.
Il s'ensuit que x=0 lui aussi.
Réciproquement le triplet satisfait l'équation proposée.
Conclusion:
L'équation adment donc une solution unique qui n'est autre que le triplet .
Sauf erreur.

Je propose une inégalité faisant intervenir des entiers naturels:
Problème 102:
Soit n un entier naturel non nul.
Démontrez que: .
Bonne chance.

tu dois citer que n est un entier naturel car on parle de factoriel que pour les entiers naturels. Pour démontrer on utilisera le raisonnement par récurrence je vais essayé de la résoudre aujourd'hui.