| | Marathon de l'arithmétique |  |
|
+38Liquid diablo902 judicecharatein mohamed diai kaj mima manazerty expert_run 0000 n.naoufal Calculus helloall Mehdi.O nmo Mehdi.A yasserito louis majdouline Sporovitch Matherror mizmaz Abdek_M Poincaré King M.Marjani marouan777 kholoud-tetouanie master {}{}=l'infini M.AlMokhtar Sylphaen oussama1305 Othmaann soukki tarask Dijkschneier darkpseudo kira Math=life 42 participants |
|
| Auteur | Message |
|---|
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 24 Avr 2011, 16:19 Dim 24 Avr 2011, 16:19 | |
| - Dijkschneier a écrit:
- Problème 18 : (* : une étoile)
Trouver toutes les solutions positives à l'équation diophantienne : x²+21y²=10^4 - Spoiler:
Il est clair que x et y ont la meme parité s'ils sont tous les 2 impaire on aura : 10^4=1+21[8]=6[8] contradiction.
donc ils sont tous les deux pairs , on pose x=2a ; y=2b <==> a²+21b²=2500 de meme a et b sont pairs donc a=2p ; b=2q
<==> p²+21q²=625 ==> q²=<29 ==> q£ {0,1,2,3,4,5} ==> (p=10 ,q=5) ; (p=17 ,q=4) ;( p=25 ,q=0)
donc les solutions de l'équation initiale sont : (40,20);(68,16) ; (100,0)
Problème 19 : (***) soit m>1 et PGCD(x;y)=1 (Montrer qu'il existe une infinité d'entiers x ;y tel que x|y²+m et y|x²+m
Dernière édition par Sporovitch le Lun 25 Avr 2011, 19:18, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 24 Avr 2011, 17:59 Dim 24 Avr 2011, 17:59 | |
| - Sporovitch a écrit:
Problème 19 : (**)
Soit A la somme des chiffres du nombre  et B la somme des chiffres du nombre A . Trouver la somme des chiffres du nombre B (le système de numération utilisé est le sytème décimal). et B la somme des chiffres du nombre A . Trouver la somme des chiffres du nombre B (le système de numération utilisé est le sytème décimal). Celui là est bien connu et a été déjà proposé sur ce forum. Peut-être serait-il préférable de le changer ? | |
|
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 24 Avr 2011, 18:58 Dim 24 Avr 2011, 18:58 | |
| - Dijkschneier a écrit:
- Celui là est bien connu et a été déjà proposé sur ce forum.
Peut-être serait-il préférable de le changer ? Peux-tu donner la réponse? ou au moins donner le lien. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 24 Avr 2011, 20:06 Dim 24 Avr 2011, 20:06 | |
| L'idée c'est de voir à quoi est congru s(s(s(4444^4444))) modulo 9, puis de montrer avec des majorations que s(s(s(4444^4444))) est fait d'un seul chiffre (ou de deux, je ne me rappelle plus)
s(x) désigne la somme des chiffres de x. | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 24 Avr 2011, 20:18 Dim 24 Avr 2011, 20:18 | |
| Où est passé le problème de Sporovitch ?
| |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 24 Avr 2011, 20:44 Dim 24 Avr 2011, 20:44 | |
| Solution au problème 20 disparu .... On procède par disjonction de cas : Si p=2 alors a^4=4(1-b^4)>0 => b=1 ou b=0 si b=1 alors a=0 d'où (0,1,2) est une solution . si b=0 alors a^4=4 impossible. Si p>=3posons d=a^b , dx=a , dy=b avec x^y=1 en substituant on aura d^4 (x^4+4y^4)=p^2 d'où d^4 divise p^2 alors d=1 on sait que a^4+4b^4=(a^2+2b^2-2ab)(a^2+2b^2+2ab)=p^2 on a les cas suivants : 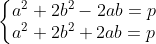 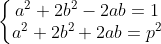 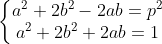 1er cas 1er cas on a a²+2b²+2ab=a²+2b²-2ab d'où ab=0 si a=0 alors 2b²=p (impossible puisque p est impair) si b=0 alors a²=p (impossible puisque p est premier) 2ème cas => (a-b)²=1-b²>=0 => b =0 ou b=1 si b=0 alors a²=1=p² impossible si b=1 alors 1-p²=4a>=0 impossible puisque p>=3 3ème cas de manière analogue à la précédente b=0 ou b=1 si b=0 on trouve une contradiction si b=1 on trouve une autre (comme fait dans le deuxième cas) Donc la seule solution est a=0 , b=1 et p=2. Edit : P.S: le d=1 n'a pas servi et on aurait pu éviter le troisième cas en remarquant que a²+2b²+2ab>=a²+2b²-2ab ... | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Lun 25 Avr 2011, 19:20 Lun 25 Avr 2011, 19:20 | |
| Problème 19 édité !
PS: il ny'avé po de problème 20 je sais pas d'ou tarask a vu le probleme 20 ? | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Lun 25 Avr 2011, 19:45 Lun 25 Avr 2011, 19:45 | |
| - Sporovitch a écrit:
- Problème 19 édité !
PS: il ny'avé po de problème 20 je sais pas d'ou tarask a vu le probleme 20 ? Je l'avais confondu avec un posté dans la section des premières (celui de Germain) . Je m'en excuse ! | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mar 26 Avr 2011, 14:49 Mar 26 Avr 2011, 14:49 | |
| - Sporovitch a écrit:
Problème 19 : (***)
soit m>1 et PGCD(x;y)=1
(Montrer qu'il existe une infinité d'entiers x ;y tel que
x|y²+m et y|x²+m Solution au problème 19 :- Spoiler:
1) x|y²+m et y|x²+m avec pgcd(x,y)=1 <===> xy | x²+y²+m avec pgcd(x,y)=1
2) Soit (x,y) un couple d'entiers positifs vérifiant xy | x²+y²+m et pgcd(x,y)=1 et x<y (ce couple existe, on peut prendre par exemple x=1 et y = m+1 > 1 = x).
Écrivons x²+y²+m=xyk, et fixons k. Notons qu'alors on a nécessairement k>2, étant donné que xyk = x²+y²+m >= 2xy + m.
Maintenant, on peut aussi écrire : x²-xyk + (y²+m)=0.
Considérons le trinôme X²-Xyk+(y²+m). Ce trinôme admet une racine x, et l'autre racine x' vérifie les relations : x+x'=yk et xx'=(y²+m).
La première relation assure que x' est un entier et que pgcd(x',y)=pgcd(yk-x,y)=pgcd(x,y)=1, et la seconde qu'il est strictement positif.
De plus, on a x'>y, car cela est équivalent à x+x' > x+y, ou encore à yk > x+y, ou encore à y(k-1)>x, ce qui est vrai étant donné que k>1 et y>x.
Ainsi, on peut répéter le processus avec le couple (y,x'), et cela produit au final une suite strictement croissante de couples solutions, et permet de conclure.
Remarque : la condition m>1 n'a pas été utilisée, alors merci de vérifier ma solution.
| |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mar 26 Avr 2011, 15:28 Mar 26 Avr 2011, 15:28 | |
| Problème 20 : (* : une étoile)
Trouver tous les entiers naturels n tels qu'il existe deux entiers a et b qui vérifient : n²=a+b et n^3 = a²+b² | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mar 26 Avr 2011, 20:46 Mar 26 Avr 2011, 20:46 | |
| on sait que (a+b)²<=2(a²+b²) ainsi n^4<=2n^3 si n=0 =>a=0 et b=0 si n=/=0 ainsi on a n<=2 alors n=2 ou n=1 n=2 est le cas d'egalite de l'inegalite (a+b)²<=2(a²+b²) qui est bien sur a =b ainsi a=b=2 n=1 alors a+b=a²+b²=1 ainsi ab=0 alors (a=0 et b=1) ou (b=0 et a=1)... sauf erreur  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 01 Mai 2011, 16:55 Dim 01 Mai 2011, 16:55 | |
| Problème 21 : (** : deux étoiles) Prouver que : (\exists%20k%20\in%20\mathbb{N})%20:%20s(k^2)=s(k)^2=n^2%C2%B2) , où s est la fonction qui à un entier associe la somme de ses chiffres. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mar 03 Mai 2011, 21:18 Mar 03 Mai 2011, 21:18 | |
| Vous pouvez trouver une solution ici : http://www.artofproblemsolving.com/Forum/viewtopic.php?f=57&t=404745
Problème 22 : (** : deux étoiles)
Soient b,n > 1 deux entiers. On suppose que pour tout k > 1, il existe un entier a_k tel que b - (a_k)^n est divisible par k. Prouver que b=A^n, pour un certain entier A. | |
|
  | |
Abdek_M
Maître

 Nombre de messages : 162 Nombre de messages : 162
Age : 31
Localisation : France
Date d'inscription : 18/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mar 03 Mai 2011, 23:38 Mar 03 Mai 2011, 23:38 | |
| Solution:Soit  un diviseur premier de  et soit  la plus grande puissance telle que  ,alors d'après l'hypothèse il existe un entier  tel que  comme  alors  donc  est un diviseur premier de  posons donc  ou  est un entier non divisible par  et comme  alors  , et d'autre part  donc cela impose que  et donc  finalement  et Ainsi pour tout diviseur premier  de  ,  est un multiple de  et d'ou le resultat voulu. Je propose ce joli problème :
Montrer que tout entier naturel n peut s'ecrire comme la difference de deux entiers naturels qui ont le même nombre de diviseurs premiers. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mer 04 Mai 2011, 23:52 Mer 04 Mai 2011, 23:52 | |
| Solution : - Spoiler:
Posons d(n)=le nombres de diviseur premier de n . Si n est paire alors d(2n)=d(n) et n=2n-n Donc n vérifie la propriété (P) : n peut s'ecrire comme la difference de deux entiers naturels qui ont le même nombre de diviseurs premiers. Soit 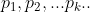 la suite des nombres premiers avec p 1=3 . On va montrer que si n est impaire et ne vérifie pas la propriété (P) alors : 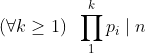 On raisonne par récurrence . Soit n un entier impaire Si n n'est pas divisible par 3 alors d(3n)=d(2n)=d(n)+1 et 3n-2n=n donc n vérifie la propriété (P) , Par conséquent si n ne vérifie pas (P) alors 3|n . Supposons que 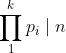 et montrons que : 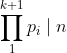 Pour cela on suppose que p k+1 ne divise pas n et on montre que n vérifie (P) . supposons que p k+1 ne divise pas n . Posons : 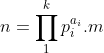 Avec m un entier qui est soit ègal à 1 soit que tous ses diviseur premiers sont supérieur ou égal à p k+2. On sait que : 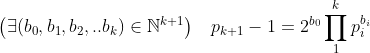 avec b 0 différent de 0 . Et puisque : 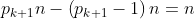 Et : 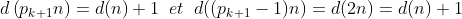 alors n vérifie (P) . Enfin on a démontré que si n ne vérifie pas (P) il est divisible par tous les nombres premier . par conséquent tous les entiers >0 vérifient la propriété (P) .
Problème 24 : Soit a 1,a 2..a n des entiers strictement positifs et deux à deux distincts.(n>2) Montrer qu'il existe deux indices distincts i et j t.q a i+a j ne divise aucun des nombres 3a 1,3a 2..3a n | |
|
  | |
Abdek_M
Maître

 Nombre de messages : 162 Nombre de messages : 162
Age : 31
Localisation : France
Date d'inscription : 18/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Sam 07 Mai 2011, 11:56 Sam 07 Mai 2011, 11:56 | |
| Raisonnons par recurrence , l'initialisation est facilement traitée, maintenant soient  des entiers positifs deux à deux distincts , si pour tout  et  ,  alors pour tout  ,  donc pour tout  ,  ainsi comme les relations de divisiblités sont homogènes on peut remplacer les  par les  et du coup sans perte de generalité on peut travailler avec des  tel qu'il existe  non divisible par  et supposons  par l'abrsurde supposons que l'hypothèse est fausse pour n+1 ainsi il existe  tel que  et comme  alors  et donc  , pour tout  il existe  tel que  ainsi pour tout  compris entre 1 et n+1 il existe un entier  tel que ,  il est immédiat que les  ne peuvent pas dépasser  maintenant si il existe  tel que  et  il en resulte que  ,maintenant appliquons l'hypothèse de recurrence sur tous les  sauf  ainsi on peut dire qu'il existe r1 et r2 tels que  pour tout  différent de  en particulier comme  alors  car  et donc l'hypothèse est vrai dans ce cas ce qui est absurde...le cas ou  alors  est la seule valeur possible i.e  et ainsi on peut refaire la même chose en appliquant l'hypothèse tous les  sauf  ce qui est absurde...sinon alors donnons nous une application  définie par  il est donc clair que  est bien définie sur l'ensemble des  dans  si  n'est pas surjective ,alors par le principe des tiroirs il existe  et  distincts tel que  i.e  en supposons  alors cela implique que  ce qui est impossible car  , ....donc prenons un élement  tel que  comme  et que  alors  ce qui est absurde... | |
|
  | |
Abdek_M
Maître

 Nombre de messages : 162 Nombre de messages : 162
Age : 31
Localisation : France
Date d'inscription : 18/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 08 Mai 2011, 11:54 Dim 08 Mai 2011, 11:54 | |
| Problème 25 Existe-il un entier positif  ayant exactement 2011 diviseurs premiers et  divise  ? | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Lun 23 Mai 2011, 23:18 Lun 23 Mai 2011, 23:18 | |
|
Dernière édition par Dijkschneier le Ven 27 Mai 2011, 15:12, édité 2 fois (Raison : Problème non convenable) | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mar 24 Mai 2011, 14:38 Mar 24 Mai 2011, 14:38 | |
| Pour le problème 25 :
On démontre par une récurrence assez aisé que le nombre (2^(3^n)+1) est divisible par 3^n , ensuite par une autre récurrence que (2^(3^n)+1) admet n diviseurs premiers distincts le reste est trivial .
PS: l'idée des puissances de 3 m'as été donné par un ami donc c'est pas vraiment ma solution .
Amicalement
Dernière édition par darkpseudo le Jeu 26 Mai 2011, 18:33, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Jeu 26 Mai 2011, 18:26 Jeu 26 Mai 2011, 18:26 | |
| - Citation :
- ensuite par une autre récurrence que (2^(3^n)+1) admet n diviseurs premiers distincts
En fait, ce n'est pas vrai. | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Jeu 26 Mai 2011, 18:45 Jeu 26 Mai 2011, 18:45 | |
| Pour n =1 c'est vrai supposons que c'est vrai pour n et prouvons le pour n+1 . On a :  de plus :  D'ou leurs PGCD = 3 et vu que 9 divise le second , alors notre rapport accepte bien un diviseur premier différent des n autres CQFD . | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Jeu 26 Mai 2011, 19:04 Jeu 26 Mai 2011, 19:04 | |
| Au moins un, mais pas exactement 1. | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Jeu 26 Mai 2011, 19:09 Jeu 26 Mai 2011, 19:09 | |
| J'ai jamais dis exactement  . | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 05 Juin 2011, 19:56 Dim 05 Juin 2011, 19:56 | |
| Donc comme problème 26, je propose :
Problème 26 : (*** : trois étoiles)
On définit une suite (a_n)_(n>=0) de la façon suivante :
a_0 = 1
a_(n+1) = (a_n)/2 si a_n est pair
a_(n+1) = a_n + d si a_n est impair
Trouver tous les entiers strictement positifs d tels qu'il existe un entier i non nul tel que a_i = 1.
| |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 05 Juin 2011, 20:47 Dim 05 Juin 2011, 20:47 | |
| - Spoiler:
Solution au prob 26 :
Si d est paire alors (an)n≥0 est une progression arithmétique de raison d ( strictement croissante ) .
On montre que si d est impaire alors il existe i>0 t.q ai=1
Pour d=1 le résultat est vrai ..
Soit d>1 un entier impaire , on montre que :
-Si an est paire alors an < 2d
-Si an est impaire alors an <d
On raisonne par récurrence , puisque le résultat est vrai pour n=0 supposons que pour tous les entier m≤n on ait :
-am est paire =>am < 2d
-am est impaire => am <d
1) si an est paire alors an+1 = an /2 <d
Donc si an+1 est paire ou impaire la propriété est vrai
2) si an est impaire alors an+1=an+d <2d
et an+1 est paire ..
Donc on a prouvé que la suite d'entier ( an)n≥0 est bornée(car an>0 .. d'après le principe de tiroir il existe un entier k<2d t.q a2d=ak
Si k=0 on a fini sinon on montre que ak-1=a2d-1
si ak-1≠a2d-1 alors on aura soit :
ak-1+d=a2d-1 /2 ou a2d-1+d=ak-1 /2
ce qui implique que ak-1>2d ou a2d-1>2d ce qui est impossible ..
On continue ainsi pour trouver :
a2d-k=a0=1 .. ce qui achève la preuve .
Problème 27 : La suite d'entier a 1, a 2, a 3... est définit comme suit : a 1=1 et pour n>1 a n est le plus petit entier strictement supérieur à a n-1 t.q a i+ a j ≠ 3a k pour tous i,j,k dans {1,2,...n} non nécessairement distincts . Déterminer a 2011
Dernière édition par Sylphaen le Mar 07 Juin 2011, 16:35, édité 1 fois | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  | |
| |
|
  | |
| | Marathon de l'arithmétique |  |
|
