| | Marathon de l'arithmétique |  |
|
+38Liquid diablo902 judicecharatein mohamed diai kaj mima manazerty expert_run 0000 n.naoufal Calculus helloall Mehdi.O nmo Mehdi.A yasserito louis majdouline Sporovitch Matherror mizmaz Abdek_M Poincaré King M.Marjani marouan777 kholoud-tetouanie master {}{}=l'infini M.AlMokhtar Sylphaen oussama1305 Othmaann soukki tarask Dijkschneier darkpseudo kira Math=life 42 participants |
|
| Auteur | Message |
|---|
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Lun 14 Fév 2011, 19:42 Lun 14 Fév 2011, 19:42 | |
| Solution : - Spoiler:
Pour le premier on a d'après le théorème des nombres premiers : \sim&space;\frac{p_{n}}{Ln(p_{n})}&space;\Rightarrow&space;\prod_{1}^{n}\sqrt&space;{\pi&space;(p_{i})}\sim&space;\sqrt{n!}\sim&space;\frac&space;{\sqrt&space;{\prod&space;p_{i}&space;}}{\prod&space;Ln(p_i)}%3E)  Il suffit de prouver que 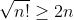 qui découle directement du fait que n>5 Pour la seconde il suffit de passer par le théorème des nombres premiers d'utilisé l'exp et d'étudié la fonction e(x)-x^2
| |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Lun 14 Fév 2011, 20:55 Lun 14 Fév 2011, 20:55 | |
| Solution du problème de sylphaen : On a : [img]http://latex.codecogs.com/gif.download?\frac{a^2}{b}+\frac{b^2}{a}-1%3C&space;\left&space;[&space;\frac{a^2}{b}&space;\right&space;]+\left&space;[&space;\frac{b^2}{a}&space;\right&space;]\leq&space;\left&space;[&space;\frac{a^2}{b}+\frac{b^2}{a}&space;\right&space;][/img] d'un coté on a : [img]http://latex.codecogs.com/gif.download?\frac{a^2}{b}+\frac{b^2}{a}-1%3C&space;\left&space;[&space;\frac{a^2+b^2}{ab}&space;+ab&space;\right&space;]&space;\Rightarrow&space;\frac{a^2}{b}+\frac{b^2}{a}-1%3C\frac{a^2+b^2}{ab}&space;+ab[/img] ^2+ab) D' autre coté on a : [img]http://latex.codecogs.com/gif.download?\left&space;[&space;\frac{a^2+b^2}&space;{ab}\right&space;]+ab&space;\leq&space;\left&space;[\frac{a^3+b^3}&space;{ab}&space;\right&space;][/img] Si cette inégalité est stricte avec 2 de plus on obtient une contradiction avec la première inégalité et donc il n'y a que 2 cas : [img]http://latex.codecogs.com/gif.download?\left&space;[&space;\frac{a^3+b^3}{ab}&space;\right&space;]=\left&space;[&space;\frac{a^2+b^2}{ab}&space;\right&space;]+ab&space;\&space;ou&space;\left&space;[&space;\frac{a^3+b^3}{ab}&space;\right&space;]=\left&space;[&space;\frac{a^2+b^2}{ab}&space;\right&space;]+ab&space;+&space;1[/img] Une étude au cas par cas permet de déterminé les solutions de ces deux équations , je dois partir maintenant donc je terminerais la rédaction plus tard . Si quelqu'un pouvais me passé un bon site de Latex svp , car le mien foir énormément . Amicalement . | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Jeu 07 Avr 2011, 23:45 Jeu 07 Avr 2011, 23:45 | |
| Redonnons du souffle à ce marathon avec un nouveau problème qui m'a été proposé par Youssef durant le stage... et qui est bien connu.
Et puisqu'aucune numérotation de problèmes n'a été donnée jusqu'à maintenant, le problème suivant serait noté arbitrairement : problème 10. Le prochain sera bien entendu le problème 11.
Problème 10 : (** : deux étoiles)
Soit x et y deux entiers et p un nombre premier congru à 3 modulo 4.
Montrer que p|x²+y² <==> p|x et p|y | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Ven 08 Avr 2011, 00:36 Ven 08 Avr 2011, 00:36 | |
| x^2 congru à -y^2 mod p donc x^(p-1) congru à (-1)^((p-1)/2)*y^(p-1) mod p
et puisque (p-1)/2 est impair x^(p-1) congru à -y^(p-1) mod p
Et si on suppose que p ne divise pas x (symétrie de role ) on a x^(p-1) congru à 1 mod p
et donc p|1 ou p|2 qui sont tout les deux des contradictions avec l'énoncé .
Problème 11 :
Prouvez que si p^n|(a^p-1) alors p^(n-1)|a-1 | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Ven 08 Avr 2011, 13:19 Ven 08 Avr 2011, 13:19 | |
| Je n'ai pas très bien compris le p divise 1 ou p divise 2, mais je voudrais noter qu'à partir du moment que l'on a y^(p-1) = -1 (mod p), avec (p-1) pair, on peut déduire que -1 est un résidu quadratique, ce qui permet de conclure avec le critère d'Euler (ou avec le lemme de Gauss) que p est congru à 1 modulo 4, contradiction... Solution au problème 11 :Puisque 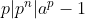 , alors d'après le lemme LTE, on a : %20=%20v_p%20(a-1)%20+%201) , qui permet de conclure que %20\geq%20n-1)
Dernière édition par Dijkschneier le Ven 08 Avr 2011, 19:03, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Ven 08 Avr 2011, 13:29 Ven 08 Avr 2011, 13:29 | |
| Par ailleurs, est-ce que le problème 10 n'est pas un cas particulier du théorème des deux carrés de Fermat ? | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Ven 08 Avr 2011, 13:46 Ven 08 Avr 2011, 13:46 | |
| Je n'est pas voulu utilisé les résidu quadratique pour que la solution soit accessible à tous ; Pour ta question on a p ne divise pas x ==> x^(p-1) = 1 [p] ( Fermat ) et donc
1 = -(y^(p-1)) [p] si p| y on a 1 = 0 mod [p] et si p ne divise pas y on a part Fermat -y^(p-1) =-1[p]
et donc 1=-1[p] CAD p|2 .
Pour ta seconde question cette exercice n'en est qu'une application direct . | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 10 Avr 2011, 16:11 Dim 10 Avr 2011, 16:11 | |
| Problème 12 : (** : deux étoiles)
Trouver tous les rationnels r et les entiers z (de Z) tels que : 2^z + 2 = r². | |
|
  | |
Matherror
Maître
 Nombre de messages : 81 Nombre de messages : 81
Age : 32
Date d'inscription : 09/04/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 10 Avr 2011, 16:59 Dim 10 Avr 2011, 16:59 | |
| - Dijkschneier a écrit:
- Problème 12 : (** : deux étoiles)
Trouver tous les rationnels r et les entiers z (de Z) tels que : 2^z + 2 = r². z # 0 car 1+2 = 3 n'est pas le carré d'un rationnel. Z+ et Z- désignent l'ensemble des entiers supérieurs strictement (resp. inférieurs strictement) à 0. z appartient à Z+ : Alors r s'écrit 4k² où k est un entier. Donc 2^(z-1) + 1 = 2k² Donc 2^(z-1) est impair. Donc z = 1. D'où les couples (2,1) et (-2,1) sont solutions. z appartient à Z- : On pose n = -z. Alors 2^(n+1) + 1 = r².2^n. Alors r s'écrit p/q avec p entier, pgcd(p,q) = 1 et q =2^k où k est un entier positif ou nul. Donc 2^(n+1) + 1 = p².2^(n-2k). Donc 2^(n-2k) = 1 et p² = 2^(n+1) + 1. Donc (p-1)(p+1) = 2^(2k+1). Donc p - 1 = 2^i et p+1 = 2^j avec i+j = 2k+1. Donc 2^j = 2^i + 2. D'où i = 1 et j = 2. D'où k = 1 et n = 2 et p² = 9. D'où les couples (3/2, -2) et (-3/2, -2) sont solutions. Conclusion : l'ensemble des solutions est {(2,1), (-2,1), (3/2, -2), (-3/2, -2)}. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 10 Avr 2011, 17:06 Dim 10 Avr 2011, 17:06 | |
| | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mar 12 Avr 2011, 11:55 Mar 12 Avr 2011, 11:55 | |
| Pour plus de concision, merci de "spoiler" les futures solutions.
Problème 13 : (* : une étoile)
Montrer que pour tout entier a > 2, a^(a-1)-1 n'est pas sans facteur carré. | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mar 12 Avr 2011, 13:02 Mar 12 Avr 2011, 13:02 | |
| Solution du problème 13 : - Spoiler:
soit p un diviseur premier de a-1 ( non nécessairement distinct de a-1 ) on a :
p|a-1 et p ne divise pas a donc par LTE :
vp(a^(a-1)-1) = 2vp(a-1) et donc p^(2k)|a^(a-1)-1 CQFD . Sauf erreur .
| |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mar 12 Avr 2011, 14:41 Mar 12 Avr 2011, 14:41 | |
| Pourquoi tu précises darkpseudo que p ne divise pas a ? Problème 14 : (* : une étoile) Soit F_n le n-ième nombre de Fermat. Prouver que : 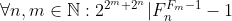 | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mar 12 Avr 2011, 15:55 Mar 12 Avr 2011, 15:55 | |
| C 'est une condition de LTE  on doit avoir p|a-b et p ne divise pas a et p ne divise pas b Solution du problème 14 : - Spoiler:
ON doit montrer que
2^(2^m)|sigma(i=0-->F(m-1)-1)Fn^(Fm-1-i) , vu que m et n ont un rôle symétrique à gauche c'est qu'ils l'ont aussi à droite donc on peut supposer que n>=m dans ce cas F(n)=1[2^(2^m)]
donc : sigma(i=0-->Fm-1-1)Fn^(Fm-1-i)=Fm-1[2^(2^m)] et Fm-1=2^(2^m) CQFD .
| |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mar 12 Avr 2011, 16:41 Mar 12 Avr 2011, 16:41 | |
| | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mar 12 Avr 2011, 16:54 Mar 12 Avr 2011, 16:54 | |
| J'ai juste écris 2^(2^m)*2^(2^n) et je me suis débarassé du 2^(2^n) en utilisant le fait que a^n-1 =(a-1)(sigma i=0->n-1 a^(n-i)) ensuite il est clair que si a=1[b] alors a^i=1[b] et aussi si n>=m on a 2^m|2^n et donc 2^(2^m)|2^(2^n) en sommant on obtient le résultat. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mar 12 Avr 2011, 17:07 Mar 12 Avr 2011, 17:07 | |
| Je ne comprends toujours pas  Pourquoi tu supposes que n >= m ? | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mar 12 Avr 2011, 21:50 Mar 12 Avr 2011, 21:50 | |
| Ok j'ai supposé n>=m pour avoir :  J'ai le droit de supposer ceci car  est une expression symétrique . Sinon je pense que ceci est la méthode la plus courte je pense . Amicalement ( Et bonne rentrée by the way ) | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mar 12 Avr 2011, 22:33 Mar 12 Avr 2011, 22:33 | |
| Désolé mais j'ai toujours pas compris ta solution puisque ça manque un peu de Latex...
De toute façon, la solution directe à laquelle je m'attendais était d'utiliser la formule du binôme... | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mar 12 Avr 2011, 22:44 Mar 12 Avr 2011, 22:44 | |
| C'est pas juste LTe ? 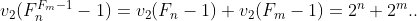 Voici un autre exo :p Déterminer les entiers n>1 qui vérifie la condition : Pour tous a,b premier avec n . 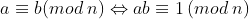 | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Ven 15 Avr 2011, 16:56 Ven 15 Avr 2011, 16:56 | |
| - Sylphaen a écrit:
Problème 15 :
Déterminer les entiers n>1 qui vérifie la condition :
Pour tous a,b premier avec n .
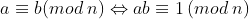 Solution au problème 15 :- Spoiler:
1) [ pour tous a,b premiers avec n : 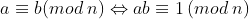 ] <===> [ pour tout a premier avec n : a²=1 (mod n) ] 2) Si n est premier avec 2, c'est qu'on a : 2²=1 (mod n), d'où n|3, d'où n=3. Inversement, n=3 marche. Si n n'est pas premier avec 2, en d'autres termes, s'il est pair, alors écrivons 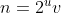 où v est impair, et remarquons qu'alors, v+2 est premier avec n (en effet, si d=pgcd(n,v+2) est différent de 1, alors -2^uv=2^{u+1}) , donc d est pair, donc v+2 a un diviseur pair, ce qui est impossible vue que v, et donc v+2 est impair). D'où : (v+2)²=1 (mod n), donc (v+2)²=1 (mod v), donc 2²=1 (mod v), donc v|3, donc v=1 ou v=3. Cela veut dire que n=2^u ou n=3.2^u et dans les deux cas, 5 est premier avec n, ce qui permet d'écrire 5²=1 (mod n), et donc n|24, et donc n=2 ou n=3 ou n=4 ou n=6 ou n=8 ou n=12 ou n=24. Inversement, tous ces nombres marchent. Synthèse :Les entiers n>1 recherchés sont les éléments de l'ensemble : {2,3,4,6,8,12,24}
| |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Sam 16 Avr 2011, 23:55 Sam 16 Avr 2011, 23:55 | |
| Problème 16 : (* : une étoile)
Trouver tous les entiers naturels a et b tels que ab | a^3 + b^3 | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Sam 23 Avr 2011, 14:17 Sam 23 Avr 2011, 14:17 | |
| Solution au problème 16 :- Spoiler:
Notons d=pgcd(a,b), et écrivons a=da' et b=db' avec pgcd(a',b')=1.
ab | a^3 + b^3 ===> a'b' | d(a'^3 + b'^3)
Or, a' | a'b' | d(a'^3 + b'^3), d'où a' | db'^3, et puisque pgcd(a',b'^3)=1, il vient a' | d
De même : b' | d
Puisque en plus pgcd(a',b')=1, on en déduit que a'b' | d
Inversement, si a et b sont deux entiers strictement positifs, et que l'on écrit d=pgcd(a,b), et a=da' et b=db' avec pgcd(a',b')=1, et que a'b' | d, alors on a : a'b' | d(a'^3 + b'^3), ce qui est équivalent à : ab | a^3 + b^3
Synthèse :
Les entiers a et b recherchés sont ceux pour lesquels a'b' | d, lorsque d=pgcd(a,b) et a=da' et b=db' avec pgcd(a',b')=1.
Que l'on peut aussi reformuler : les entiers a et b recherchés sont ceux de la forme a=a'²b't et b=a'b'²t avec pgcd(a',b')=1 et t arbitraire.
Problème 17 : (** : deux étoiles) Trouver tous les quadruplets (a,b,p,n) d'entiers strictement positifs tels que p est premier et : a^3 + b^3 = p^n
Dernière édition par Dijkschneier le Sam 23 Avr 2011, 20:44, édité 1 fois | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Sam 23 Avr 2011, 18:29 Sam 23 Avr 2011, 18:29 | |
| - Dijkschneier a écrit:
Problème 17 : (** : deux étoiles)
Trouver tous les quadruplets d'entiers strictement positifs tels que p est premier et :
a^3 + b^3 = p^n CURRENT LIFE THEOREM kills it immediately !! | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Sam 23 Avr 2011, 18:59 Sam 23 Avr 2011, 18:59 | |
| - Sporovitch a écrit:
- Dijkschneier a écrit:
Problème 17 : (** : deux étoiles)
Trouver tous les quadruplets d'entiers strictement positifs tels que p est premier et :
a^3 + b^3 = p^n CURRENT LIFE THEOREM kills it immediately !! Shhh ! Tu n'es pas censé le dire en plein public !  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  | |
| |
|
  | |
| | Marathon de l'arithmétique |  |
|
