| | Marathon de l'arithmétique |  |
|
+38Liquid diablo902 judicecharatein mohamed diai kaj mima manazerty expert_run 0000 n.naoufal Calculus helloall Mehdi.O nmo Mehdi.A yasserito louis majdouline Sporovitch Matherror mizmaz Abdek_M Poincaré King M.Marjani marouan777 kholoud-tetouanie master {}{}=l'infini M.AlMokhtar Sylphaen oussama1305 Othmaann soukki tarask Dijkschneier darkpseudo kira Math=life 42 participants |
|
| Auteur | Message |
|---|
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Ven 03 Sep 2010, 23:27 Ven 03 Sep 2010, 23:27 | |
| - Sylphaen a écrit:
- Problème 7 :
Soit p un nombre premier >2 et n un entier>1 MQ l'équation :
2p+3p=an n'admet pas de solution dans Z Quel est l'inconnu : a ou n ? | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Ven 03 Sep 2010, 23:42 Ven 03 Sep 2010, 23:42 | |
| | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 05 Sep 2010, 00:52 Dim 05 Sep 2010, 00:52 | |
| Bonsoir tout le monde  Ben je crois que les 24 heures se sont écoulées  J'avais la solution qui n'est pas la mienne parce que j'ai déjà fait face à ton exercice dans un document mais je voulais que les autres participent ....  Amicalement Sylphaen  | |
|
  | |
{}{}=l'infini
Expert sup

 Nombre de messages : 1164 Nombre de messages : 1164
Age : 32
Date d'inscription : 25/09/2008
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 05 Sep 2010, 14:21 Dim 05 Sep 2010, 14:21 | |
| - Sylphaen a écrit:
- Voici la soluce :
- Spoiler:
Soit k un entier>0 t.q p=nk+1 on a :
p |(n-1)(n²+n+1) => p |n²+n+1 puisque p>n-1
donc :
p| k(n²+n+1) -(n+1)(nk+1)=k-n-1
Il est facile de vérifie que pour n,k>1 on a : |nk+1|>|k-n-1| alors on doit avoir k=n+1 d'où :
4p-3=(2n+1)²
CQFD ..
pas forcément 6 / 2*9 ( 6 >2 ) mais 6 ne divise pas 9 ..... | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 05 Sep 2010, 14:43 Dim 05 Sep 2010, 14:43 | |
| | |
|
  | |
{}{}=l'infini
Expert sup

 Nombre de messages : 1164 Nombre de messages : 1164
Age : 32
Date d'inscription : 25/09/2008
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 05 Sep 2010, 15:10 Dim 05 Sep 2010, 15:10 | |
| oui , il a raison je me suis trompé , je m'excuse  | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 05 Sep 2010, 16:12 Dim 05 Sep 2010, 16:12 | |
| slm ,
SOLUTION :
b1 clair que p impaire ===> 2^p+3^p=5(2^p-1-3.2^p-2+......+3^p-1)
5 divise 2^p+3^p , 25 aussi !
0=2^p+3^p=5.p.2^p-1 (car 2=-3 (mod 5))
donc 5 divise p ===> 5=p
mais 2^5+3^5=275 == n'est po une puissance parfaite !
alors 2^p+3^p n'est pas une puisssance parfaite ====> n=1 ===> contradictoir car n>1
alors pas de soluc !
| |
|
  | |
kholoud-tetouanie
Habitué
 Nombre de messages : 23 Nombre de messages : 23
Age : 31
Localisation : tetouan
Date d'inscription : 15/08/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 05 Sep 2010, 16:34 Dim 05 Sep 2010, 16:34 | |
| - Spoiler:
- master a écrit:
- slm ,
SOLUTION :
b1 clair que p impaire ===> 2^p+3^p=5(2^p-1-3.2^p-2+......+3^p-1)
5 divise 2^p+3^p , 25 aussi !
0=2^p+3^p=5.p.2^p-1 (car 2=-3 (mod 5))
donc 5 divise p ===> 5=p
mais 2^5+3^5=275 == n'est po une puissance parfaite !
alors 2^p+3^p n'est pas une puisssance parfaite ====> n=1 ===> contradictoir car n>1
alors pas de soluc !
Pierre Bornsztein  P_173
Dernière édition par kholoud-tetouanie le Lun 06 Sep 2010, 00:11, édité 1 fois | |
|
  | |
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 05 Sep 2010, 16:57 Dim 05 Sep 2010, 16:57 | |
| - master a écrit:
- slm ,
SOLUTION :
b1 clair que p impaire ===> 2^p+3^p=5(2^p-1-3.2^p-2+......+3^p-1)
5 divise 2^p+3^p , 25 aussi !
0=2^p+3^p=5.p.2^p-1 (car 2=-3 (mod 5))
donc 5 divise p ===> 5=p
mais 2^5+3^5=275 == n'est po une puissance parfaite !
alors 2^p+3^p n'est pas une puisssance parfaite ====> n=1 ===> contradictoir car n>1
alors pas de soluc !
svp quelqu'un peut m'zxpliquer ce qui est en rouge ??? | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 05 Sep 2010, 18:14 Dim 05 Sep 2010, 18:14 | |
| @ KHOLOUD : ^^ je sais po si c'est ca la soluc de pierre Bronzstein mais j'ai deja travaille cet exo ! je rappell plus ou xd ^^ ! ths pour l'info ! | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 05 Sep 2010, 22:22 Dim 05 Sep 2010, 22:22 | |
| - master a écrit:
- @ KHOLOUD : ^^ je sais po si c'est ca la soluc de pierre Bronzstein mais j'ai deja travaille cet exo ! je rappell plus ou xd ^^ ! ths pour l'info !
 Bornzstein, pas Bronzstein. Ca lui plairait pas, je crois. | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 05 Sep 2010, 23:56 Dim 05 Sep 2010, 23:56 | |
| keske tu voulais dir Mr.Oussama !!!! Bornzstein ou Bronzstein c'est po l'essentiel !
c b1 vu qu'il n ya po de réponse pour l"exo du sylphaen ! c pour cela je l'ai posté, meme la soluc de cet exo est tatoué dans ma mémoire ! je rappelle plu ou je l'ai travaillé !
P.S prochaine fois etre plus sympa dans tes msg svp !
A+ Bon jeu !
| |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Ven 10 Sep 2010, 22:28 Ven 10 Sep 2010, 22:28 | |
| Bon, ce genre de discussions ne fait qu'aggraver la situation de ce forum qui vit dernièrement des temps de misère  Voilà cet exercice pour remettre le marathon en ordre :  Bonne chance  | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Sam 11 Sep 2010, 23:11 Sam 11 Sep 2010, 23:11 | |
| Personne ?  je vais pas poster une solution .... | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 12 Sep 2010, 02:13 Dim 12 Sep 2010, 02:13 | |
| @Marouane777:
Contre exemple: T'as dis que 2^n+1 = 3+kn
n=4 ===> 2^n+1 = 3 +kn => 2^4+1 = 3 +4k
=> k=(17-3) / 4 = 14/4 qui n'apartient pas à IN ... donc k n'apartient à IN.
Donc la solution que vous venez de nous donner est fausse, désolé et essaye autrement.
EDIT: Marouane777 a supprimé son poste. | |
|
  | |
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 12 Sep 2010, 02:28 Dim 12 Sep 2010, 02:28 | |
| oui c'est fait.mais la suppression etait avant ta remarque =) | |
|
  | |
King
Maître

 Nombre de messages : 125 Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 12 Sep 2010, 02:34 Dim 12 Sep 2010, 02:34 | |
| La relation de Marouan777 est vrai si et seulement si l'entier est premier.
A 2H du matin, il y a de fortes chances de commettre des fautes comme ça, ça arrive c'est normal... | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 12 Sep 2010, 04:02 Dim 12 Sep 2010, 04:02 | |
| @ Marouane: Comme l'a dis King que c'est déjà 2h .. :d
Ma premiére participation : )
Ma Solution: (Du probléme n° 8):
* n^2 | 2^n + 1 (n Impaire) alors (n-1)(n+1) | 2^n ==> n-1 | 2^n ou n+1 | 2^n
n=2k+1 ==> 4k(k+1) | 2^{2k+1} == (2t=k(k+1) ==> 2k(k+1) | 4^k=2*2^{k-1}
=> k(k+1) | 2^{k-1} ,( k=1 --> n=3 solution évidente..)
* k(k+1) | 2^{k-1} => k²+k - t*2^{k-1) = 0 on aura donc aprés Delta et simplifications que t*2^{k-1}=a²-1 ===> t*2^{k-1}=8k' , alors k(k+1) | 8k'
* On a met: n=2k+1 ==> k=(n-1)/2 alors (n-1)(n+1)/(2*2) = 8k' ==> n²=4*8k'+1 qui est juste si et si que k'=0 (t=0) ==> |k|=1 ==> n=3
* Donc S={3} | |
|
  | |
King
Maître

 Nombre de messages : 125 Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 12 Sep 2010, 04:29 Dim 12 Sep 2010, 04:29 | |
| - M.Marjani a écrit:
- @ Marouane: Comme l'a dis King que c'est déjà 2h .. :d
Ma premiére participation : )
Ma Solution: (Du probléme n° 8):
* n^2 | 2^n + 1 (n Impaire) alors (n-1)(n+1) | 2^n ==> n-1 | 2^n ou n+1 | 2^n
n=2k+1 ==> 4k(k+1) | 2^{2k+1} == (2t=k(k+1) ==> 2k(k+1) | 4^k=2*2^{k-1}
=> k(k+1) | 2^{k-1} ,( k=1 --> n=3 solution évidente..)
* k(k+1) | 2^{k-1} => k²+k - t*2^{k-1) = 0 on aura donc aprés Delta et simplifications que t*2^{k-1}=a²-1 ===> t*2^{k-1}=8k' , alors k(k+1) | 8k'
* On a met: n=2k+1 ==> k=(n-1)/2 alors (n-1)(n+1)/(2*2) = 8k' ==> n²=4*8k'+1 qui est juste si et si que k'=0 (t=0) ==> |k|=1 ==> n=3
* Donc S={3} ??? | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 12 Sep 2010, 12:59 Dim 12 Sep 2010, 12:59 | |
| ma soluc : si n pair on aura : pair|impaire ==> ce qui est impossible , donc n est impaire . n a un facteur premier et impaire , suppose que ce facteur est P , alors  il ya un lemme et son nom est :"Lifting Exponents Lemma" qui définie ||x||_p comme plus grande puissance de P qui divise X , cela signifie que si  alors  ,mais  , par cette lemme on prouve ca : x,n,y £N^3 , et p est nombre premier impaire t.q : p|x+y mais  et  , alors on a :  ce qui conduit a :  si P#3 ==>  ===> contradictoire car nous avions  alors p=3 , nous supposons que p peut etre un facteur principale de n , nous avons n=3 alors S={3} | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 12 Sep 2010, 13:12 Dim 12 Sep 2010, 13:12 | |
| - master a écrit:
- ma soluc :
si n pair on aura : pair|impaire ==> ce qui est impossible , donc n est impaire .
n a un facteur premier et impaire , suppose que ce facteur est P , alors 
il ya un lemme et son nom est :"Lifting Exponents Lemma" qui définie ||x||_p comme plus grande puissance de P qui divise X , cela signifie que si  alors alors
 ,mais ,mais  , par cette lemme on prouve ca : , par cette lemme on prouve ca :
x,n,y £N^3 , et p est nombre premier impaire t.q : p|x+y mais  et et  , alors on a : , alors on a :

ce qui conduit a :

si P#3 ==> ===> contradictoire car nous avions ===> contradictoire car nous avions 
alors p=3 , nous supposons que p peut etre un facteur principale de n , nous avons n=3
alors S={3} Je viens de lire les grandes lignes de ta démonstration , faute de temps , et je crois qu'elle est juste , mais j'ai une question si vous le permettez Master , "lifting exponents" fait-il partie du programme des olympiades ?  | |
|
  | |
King
Maître

 Nombre de messages : 125 Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 12 Sep 2010, 15:15 Dim 12 Sep 2010, 15:15 | |
| En effet, "lifting exponents" ou les valuations p-adiques font partie du programme des Olymps. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 12 Sep 2010, 15:20 Dim 12 Sep 2010, 15:20 | |
| - tarask a écrit:
- Bon, ce genre de discussions ne fait qu'aggraver la situation de ce forum qui vit dernièrement des temps de misère

Voilà cet exercice pour remettre le marathon en ordre :

Bonne chance  Solution : - Lemme utilisée:
Lemme1 : Soit n>1 un entier alors n| 2 n+1 => 3|n . Preuve : Soit p>2 le plus petit diviseur premier de n et soit k l'ordre de 2 modulo p alors on a : 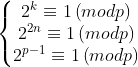 Cela implique qu'on ait : k | p-1 et k|2n donc k | PGCD(p-1,2n)=2 puisque p-1 est premier à n . Si k=1 on doit avoir 2≡1[p] ce qui est impossible donc k=2 et 4≡1[p] et donc p=3 . Fin du lemme1 . Lemme2:Notons v_p{n} la valuation_p_adique de n . Soit a un entier>0 et premier avec 3 et 2 et k un entier positif alors on a : 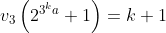 Preuve : On procède par récurrence , pour k=0 on doit prouver que : 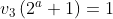 Ce qui est trivial avec les congruences modulo 9 .. Maintenant supposons que cette proposition est vrai au rang k et prouvant qu'elle est vrai aussi au rang k+1 . On a : 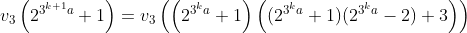  Ce qui achève la preuve ..
- Spoiler:
Maintenant revenons à notre problème . Clairement n doit être impair ..Soit k la valuation 3_adique de n , alors il existe un entier a non divisible par 3 ni par 2 t.q : n=3 ka et on a : 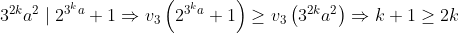 et puisque n est divisible par 3 (lemme1) alors on a : k=1 . donc n=3a avec a premier à 6 . Supposons qu'on a a>1 alors a admet un diviseur premier supérieur à 5.soit p le plus petit diviseur premier de a et s l'ordre de 8 modulo p alors on a : 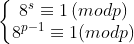 on a aussi : p| 8 a+1 => 8 2a≡1[p] et donc : s|p-1 et s|2a => s| pgcd(p-1,2a)=2=> s=1,2 dans les2 cas on obtient p=7 mais on a : 8 a+1≡2[7] ce qui crée une contradiction et donc a=1 .finalement le seul entier qui répond au problème est n=3. Désolé si c'est long -_- sinon je veux bien voir ta solution Tarask si tu veux
| |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 12 Sep 2010, 15:42 Dim 12 Sep 2010, 15:42 | |
| - Sylphaen a écrit:
- tarask a écrit:
- Bon, ce genre de discussions ne fait qu'aggraver la situation de ce forum qui vit dernièrement des temps de misère

Voilà cet exercice pour remettre le marathon en ordre :

Bonne chance 
Solution :
- Lemme utilisée:
Lemme1 : Soit n>1 un entier alors n| 2 n+1 => 3|n . Preuve : Soit p>2 le plus petit diviseur premier de n et soit k l'ordre de 2 modulo p alors on a : 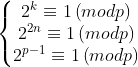 Cela implique qu'on ait : k | p-1 et k|2n donc k | PGCD(p-1,2n)=2 puisque p-1 est premier à n . Si k=1 on doit avoir 2≡1[p] ce qui est impossible donc k=2 et 4≡1[p] et donc p=3 . Fin du lemme1 . Lemme2:Notons v_p{n} la valuation_p_adique de n . Soit a un entier>0 et premier avec 3 et 2 et k un entier positif alors on a : 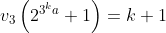 Preuve : On procède par récurrence , pour k=0 on doit prouver que : 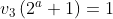 Ce qui est trivial avec les congruences modulo 9 .. Maintenant supposons que cette proposition est vrai au rang k et prouvant qu'elle est vrai aussi au rang k+1 . On a : 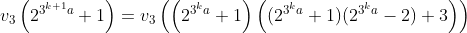  Ce qui achève la preuve ..
- Spoiler:
Maintenant revenons à notre problème . Clairement n doit être impair ..Soit k la valuation 3_adique de n , alors il existe un entier a non divisible par 3 ni par 2 t.q : n=3 ka et on a : 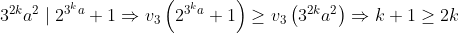 et puisque n est divisible par 3 (lemme1) alors on a : k=1 . donc n=3a avec a premier à 6 . Supposons qu'on a a>1 alors a admet un diviseur premier supérieur à 5.soit p le plus petit diviseur premier de a et s l'ordre de 8 modulo p alors on a : 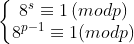 on a aussi : p| 8 a+1 => 8 2a≡1[p] et donc : s|p-1 et s|2a => s| pgcd(p-1,2a)=2=> s=1,2 dans les2 cas on obtient p=7 mais on a : 8 a+1≡2[7] ce qui crée une contradiction et donc a=1 .finalement le seul entier qui répond au problème est n=3. Désolé si c'est long -_- sinon je veux bien voir ta solution Tarask si tu veux
Bon après-midi tout le monde  merci pour votre intérêt  @Sylphaen : En effet c'est l'IMO 1990 , je cherchais des méthodes d'arithmétique efficaces et j'ai trouvé ce pdf (d'où j'ai pris l'exercice  ) et que je me permets de partager avec vous : http://reflections.awesomemath.org/2007_3/Lifting_the_exponent.pdf J'espère que ça fera l'affaire sylphaen , pour la solution propre à moi , je n'en ai pas à cet instant , je n'ai pas consacré de temps pour l'exercice  chose que je ferai plutard  | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Dim 12 Sep 2010, 20:22 Dim 12 Sep 2010, 20:22 | |
| Ah oik , Merci pour ton intérêt toi aussi .En tous cas je n'ai pas de problèmes intéressants à proposer pour le moment , je vous laisse faire .. ;p | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  | |
| |
|
  | |
| | Marathon de l'arithmétique |  |
|
