Marathon de l'arithmétique

Désolé les amis mais j'ai pas de problème à vous proposer
Je laisse quelqu'un d'autre le faire

EX N°:

Spoiler:

Bonne chance

Math=life a écrit:

EX N°:

Spoiler:

Bonne chance

@ Math=life :Avez-vous une solution ?

Problème facile :
Résoudre les deux équations diophantiennes dans N^3 :
1)x²y+y²z+z²x=3xyz
2)x^3+y^3=(x+y)²

C'est un exercice à la portée , donc n'hésitez pas à y répondre

1) Selon l'IAG, on a x²y + y²z + z²x >= 3xyz avec égalité ssi x²y=y²z=z²x, i.e., x²=yz et y²=xz et z²=xy.
Puisque on est dans le cas d'égalité, alors x²=yz et y²=xz et z²=xy, et en sommant : x²+y²+z²=xy+xz+yz.
Or on a x²+y²+z²>=xy+xz+yz avec égalité ssi x=y=z, et puisqu'on est dans le cas d'égalité, alors x=y=z.
Inversement, tous les triplets d'entiers naturels (k,k,k) sont solutions à l'équation diophantienne.
2) x^3+y^3=(x+y)² <=> x²+y²-xy = x+y.
Or x²+y²-xy >= xy d'après l'IAG, donc x+y >= xy.
Or xy croit plus rapidement que x+y lorsque x et y sont entiers >=2, donc x+y >= xy ne doit être vérifiée que pour de petites valeurs.
En effet, si x et y sont >= 2 :
x+y >= xy
<=> x(1-y) + y - 1 >= -1
<=> (y-1)(1-x) >= -1
<=> (x-1)(y-1)<=1
<=> (x,y)=(2,2)
Et on vérifie à la main que si x ou y sont < 2, alors les seuls couples qui marchent sont :
(0,0), (1,0), (0,1), (1,1), (1,2), (2,1)
Par conséquent, les solutions sont tous les couples (m,n) d'entiers naturels tels que m,n <= 2.

Dijkschneier a écrit:

1) Selon l'IAG, on a x²y + y²z + z²x >= 3xyz avec égalité ssi x²y=y²z=z²x, i.e., x²=yz et y²=xz et z²=xy.
Puisque on est dans le cas d'égalité, alors x²=yz et y²=xz et z²=xy, et en sommant : x²+y²+z²=xy+xz+yz.
Or on a x²+y²+z²>=xy+xz+yz avec égalité ssi x=y=z, et puisqu'on est dans le cas d'égalité, alors x=y=z.
Inversement, tous les triplets d'entiers naturels (k,k,k) sont solutions à l'équation diophantienne.
2) x^3+y^3=(x+y)² <=> x²+y²-xy = x+y.
Or x²+y²-xy >= xy d'après l'IAG, donc x+y >= xy.
Or xy croit plus rapidement que x+y lorsque x et y sont entiers >=2, donc x+y >= xy ne doit être vérifiée que pour de petites valeurs.
En effet, si x et y sont >= 2 :
x+y >= xy
<=> x(1-y) + y - 1 >= -1
<=> (y-1)(1-x) >= -1
<=> (x-1)(y-1)<=1
<=> (x,y)=(2,2)
Et on vérifie à la main que si x ou y sont < 2, alors les seuls couples qui marchent sont :
(0,0), (1,0), (0,1), (1,1), (1,2), (2,1)
Par conséquent, les solutions sont tous les couples (m,n) d'entiers naturels tels que m,n <= 2.

Parfait !
La première solution est la même que la mienne .
Pour la deuxième , voilà ma solution pour les intéressés :
x^3+y^3=(x+y)² <=> x²+y²-xy = x+y
Notons que si (x,y) appartient à S alors (y,x) aussi.
posons maintenant x+y=u et x-y=v alors l'équation devient équivalente à 3v²=4u-u²
or 3v² est positif alors on devrait avoir 4u-u²>=0 soit u £ {0,1,2,3,4}
en testant ces cas-là , on retrouve aisément les solutions précédemment trouvées par Dijkschneier .

P.S: A toi de poster un exercice

Très bien tarask.
Je suis désolé mais je n'ai pas de problème en arithmétique à proposer pour le moment.

Dijkschneier a écrit:

Très bien tarask.
Je suis désolé mais je n'ai pas de problème en arithmétique à proposer pour le moment.

Pas grave , je m'en charge
Voici un que je viens de trouver et qui semble intéressant :
Soit p un nombre premier >=3 , montrez , sans avoir recourt au théorème de Dirichlet , qu'il existe une infinité de nombre premiers de la forme 2pk+1 .
Hard luck

: désigne nombres premiers

problème: 1
montrer que on a :
problème: 2
montrer que :
1- et
2- et

Poincaré a écrit:

: désigne nombres premiers

problème: 1
montrer que on a :
problème: 2
1- et
2- et

Bonsoir "poincaré "
Sans vouloir être impoli , mon problème n'est pas encore résolu .
Tu dois lire les règles avant de poster
Gentiment

pardon Je ne faisais pas attention
quand on complete ton problème puis on peux voir mon problème

Solution du problème de Tarask
Supposons qu'il n'existe qu'un nombre fini de nombres premiers de la forme maintenant soit un entier tel que est impair et premier avec il suffit de prendre tel que et qui existe selon le theoreme chinois et soit un diviseur premier de il est clair donc que est impair et n'est pas parmi les c'est à dire que il s'ensuit que si est l'ordre de alors il en resulte que donc d'aprés le théoreme de Fermat et comme alors en contradiction avec le fait que est exclut des

Bonsoir :
Pour le problème de Tarask vu que Dirichlet fait de très bien l'affaire je ne me suis pas cassé la tête pour trouvé une autre solution .

Pour les problèmes de Poincaré :
Problème 1 :
procédons par récurrence :
Pour 0 c'est juste supposons que c'est vrai pour n et montrons que c'est vrai pour n-1
On a 64|5^n-8n^2+4-1 donc si elle divise 64|5^(n+1)-8(n+1)^2+4n+3 c'est que 64 | 4*5^n-16n-4 = 4( 5^n-4n-1) et donc ceci implique que 16| 5^n-4n-1 <==> 16| 4*(5^(n-1) -n)+ 4 * ( 5^(n-2)+5^(n-3)+....+1) <==> 4 |( 5^(n-1)+5^(n-2)....+1-n) qui est clairement vrai .


Pour le second :
si p est premier c'est qu'il est congru à 2 ou 1 modulo 3 or 8p-1 est lui aussi congru à 2 ou 1 modulo 3 :
si p est congru à 2 c'est que 8p-1 est divisible par 3 ce qui est contradictoire , donc p est congru à 1 et dans ce cas 8p-1 est lui aussi congru à 1 et donc 8p+1 est divisible par 3 ce qui conclut .

Pour le troisième
p^2 est toujours congru à 1 modulo 3 donc 8p^2+1 est toujours divisible par 3

Et prière de poster des exercices un peu moins à la portée .

Abdek_M a écrit:

Solution du problème de Tarask
Supposons qu'il n'existe qu'un nombre fini de nombres premiers de la forme maintenant soit un entier tel que est impair et premier avec il suffit de prendre tel que et qui existe selon le theoreme chinois et soit un diviseur premier de il est clair donc que est impair et n'est pas parmi les c'est à dire que il s'ensuit que si est l'ordre de alors il en resulte que donc d'aprés le théoreme de Fermat et comme alors en contradiction avec le fait que est exclut des

Bonsoir , je n'est pas compris quelques chose , comment pouvons nous être sûr de l'existence de P_n+1 ??

darkpseudo a écrit:

Abdek_M a écrit:

Solution du problème de Tarask
Supposons qu'il n'existe qu'un nombre fini de nombres premiers de la forme maintenant soit un entier tel que est impair et premier avec il suffit de prendre tel que et qui existe selon le theoreme chinois et soit un diviseur premier de il est clair donc que est impair et n'est pas parmi les c'est à dire que il s'ensuit que si est l'ordre de alors il en resulte que donc d'aprés le théoreme de Fermat et comme alors en contradiction avec le fait que est exclut des

Bonsoir , je n'est pas compris quelques chose , comment pouvons nous être sûr de l'existence de P_n+1 ??

même question ...

je crois que c'est immédiat puisque tout entier naturel >1 admet un diviseur premier..

:p qui peut être lui même , au fait la faute vient de moi , j'aurais du posé la question plus rigoureusement .
Qui nous dit que tout les lambda^p-1 ne sont pas premier , et donc dans ce cas on aurait p | lambda^p-2 ( sauf erreur ) ce qui inclue que p ne divise pas lambda^p-1 .
Je sais que ça paraît plus ou moins illogique que tout ces nombres soit premiers , mais une preuve est une preuve et ce cas doit être étudié à mon humble avis .

Je ne vois pas ou est le problème, si p n'est pas un diviseur de lambda^p -1 alors ou est la contradiction ?? et même si lambda^p -1 est premier la solution restera toujours valable...il vaut mieux lire attentivement la solution...

Si lambda^p-1 est premier , il n'est pas divisible par p , et on aurait P_n+1 = lambda^p-1 donc p ne divise pas P_n+1 et donc même si P_n+1 est premier il n'est malheureusement pas de la forme 2kp + 1 !!

Problème :
Trouvez tous les nombres n pour lesquels on peut décomposer l'ensemble {1,2,3,...,4n} en n sous-ensembles disjoints à quatre éléments tels que dans chaque sous-ensemble un élément est la moyenne arithmétique des trois autres.

Solution
on va commencer par montrer que si vérifie la question alors est pair , en la supposons donc pour un certain entier naturel alors il existe deux a deux distincts vérifiant pour tout , il en resulte que

ainsi n est pair ,
supposons la relation pour un certain rang comme
et

donc la relation est vrai pour l'initialisation étant évidente le resultat en découle

Abdek_M a écrit:

Solution
on va commencer par montrer que si vérifie la question alors est pair , en la supposons donc pour un certain entier naturel alors il existe deux a deux distincts vérifiant pour tout , il en resulte que

ainsi n est pair ,
supposons la relation pour un certain rang comme
et

donc la relation est vrai pour l'initialisation étant évidente le resultat en découle

Exact !
A toi maintenant, je suppose...

Ok ! je propose un problème simple mais joli
Si est le nième nombre premier , montrer que pour tout on a

où

désigne le nombre de nombres premier inférieur ou égale à n
et Montrer aussi que pour tt réel lambda>3

Pour la 1ére inégalité on raisonne par récurrence .Pour n=6 on vérifie l'inégalité .. Supposons qu'on a

Puisque n>5 on a :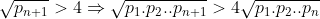
Et puisque pour tous entier n>1 il existe un nombre premier dans l'intervalle [n+1,2n-1]
Alors dans l'intervalle [n+1,4n-1] on peut trouver au moins 2 nombres premier .
Soit x un réel > 2 et p sa partie entière alors il existe 2 nombres premier dans l'intervalle [p+1,4p-1] qui est inclus dans [x,4x] . d'où :
.

Pour l'inégalité 2 on remarque qu'il suffit de prouver que pour tous n>2 on a :

Soit k un entier ( p_n≤k<p_n+1 ) où p_n est le nième nombre premier .
on a :



Alors il suffit de prouver que :
n>ln(p_n)+1
Ce qui est facilement faisable par récurrence vu que :
ln(p_n+1)+1<ln(p_n)+2<n+1

Sauf erreur ..


J'ai pas vraiment un problème intéressant à proposer mais bon voici 1 :

Trouver tous les entiers positifs a,b t.q :