| | Marathon de l'arithmétique |  |
|
+38Liquid diablo902 judicecharatein mohamed diai kaj mima manazerty expert_run 0000 n.naoufal Calculus helloall Mehdi.O nmo Mehdi.A yasserito louis majdouline Sporovitch Matherror mizmaz Abdek_M Poincaré King M.Marjani marouan777 kholoud-tetouanie master {}{}=l'infini M.AlMokhtar Sylphaen oussama1305 Othmaann soukki tarask Dijkschneier darkpseudo kira Math=life 42 participants |
|
| Auteur | Message |
|---|
Math=life
Maître
 Nombre de messages : 105 Nombre de messages : 105
Age : 33
Date d'inscription : 12/02/2010
 |  Sujet: Marathon de l'arithmétique Sujet: Marathon de l'arithmétique  Mer 01 Sep 2010, 16:49 Mer 01 Sep 2010, 16:49 | |
| TT comme les autres marathon qu'on a vu se créer ces derniers jours, je vous propose un marathon d'exercices d'arithmétique, regroupants l'arithmétique modulaire et élémentaire, en bien respectant les règles déja postées au début des autres marathons.
Bonne Chance!
Je commence par cette simple équation:
Résoudre dans Z*Z l'équation:
12x+5y=19 | |
|
  | |
kira
Maître

 Nombre de messages : 152 Nombre de messages : 152
Age : 32
Localisation : casablanca
Date d'inscription : 15/05/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mer 01 Sep 2010, 17:53 Mer 01 Sep 2010, 17:53 | |
| une solution de l'equation 12x+5y=1 donne comme solution particuliere (-2,5)
une solution particuliere de l'equation 12x+5y=19 donne ainsi (-38,95)
ceci dis l'equation 12x+5y=19 a comme solution générale (-38+5k ,95+38k) avec k£Z !!!
| |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mer 01 Sep 2010, 17:58 Mer 01 Sep 2010, 17:58 | |
| - kira a écrit:
- une solution de l'equation 12x+5y=1 donne comme solution particuliere (-2,5)
une solution particuliere de l'equation 12x+5y=19 donne ainsi (-38,95)
ceci dis l'equation 12x+5y=19 a comme solution générale (-38+5k ,95+38k) avec k£Z !!!
Pour k=8 c'est faux , et il y a d'autres contre-exemples . réponse de l'exercice 1 : - Spoiler:
(-38+5k;95-12k) c'est la réponse je pense ;
A moi ,Exercice 2 resolvez l'equation : x^6+3x^3+1=y^4 dans Z^2
Dernière édition par darkpseudo le Mer 01 Sep 2010, 23:10, édité 2 fois | |
|
  | |
kira
Maître

 Nombre de messages : 152 Nombre de messages : 152
Age : 32
Localisation : casablanca
Date d'inscription : 15/05/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mer 01 Sep 2010, 18:09 Mer 01 Sep 2010, 18:09 | |
| - darkpseudo a écrit:
- kira a écrit:
- une solution de l'equation 12x+5y=1 donne comme solution particuliere (-2,5)
une solution particuliere de l'equation 12x+5y=19 donne ainsi (-38,95)
ceci dis l'equation 12x+5y=19 a comme solution générale (-38+5k ,95+38k) avec k£Z !!!
Pour k=8 c'est faux , et il y a d'autres contre-exemples . ceci dis l'equation 12x+5y=19 a comme solution générale (-38+5k ,95-12k) avec k£Z !!!  sauf erreur je propose cet exo resoudre dans Z  ²+y²+z²=x²y² | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mer 01 Sep 2010, 18:31 Mer 01 Sep 2010, 18:31 | |
| Vous ne vous en sortirez pas si vous ne numérotez pas les problèmes et ne spécifiez pas exactement les règles du marathon.
Il est très courant que de tels marathons dont les bases ne sont pas consolidées tombent très rapidement en cours de route. | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mer 01 Sep 2010, 18:46 Mer 01 Sep 2010, 18:46 | |
| Voila je pense : Réponse de l'exercice 3 - Spoiler:
D'abord les nombres sont pair ( facil a prouver en modulo 4 )
ensuite on a x=y=z=0 est une solution :
puis x²-x²y²+y²+z² = 0
x²(y²-1) = y²+z²
donc y²-1/z²+1
or ceci reviendrait à dire que y-1/z²+1 et y+1/z²+1
je pense que dès lors la réponse est clair
Dernière édition par darkpseudo le Mer 01 Sep 2010, 23:17, édité 1 fois | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mer 01 Sep 2010, 22:04 Mer 01 Sep 2010, 22:04 | |
| - Dijkschneier a écrit:
- Vous ne vous en sortirez pas si vous ne numérotez pas les problèmes et ne spécifiez pas exactement les règles du marathon.
Il est très courant que de tels marathons dont les bases ne sont pas consolidées tombent très rapidement en cours de route. Bien dit  j'encourage l'idée de ce marathon mais j'invite M.Math=life à poser des règles (même s'il a parlé des règles des autres marathons  ) et je crois qu'il s'avère impératif d'éditer les messages de Math=life , Kira et darkpseudo en spoilant les réponses et en numérotant les exercices ! Amicalement en espérant que le marathon aura un grand succès  | |
|
  | |
Math=life
Maître
 Nombre de messages : 105 Nombre de messages : 105
Age : 33
Date d'inscription : 12/02/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Mer 01 Sep 2010, 22:42 Mer 01 Sep 2010, 22:42 | |
| Suite a vos conseil, je procède à annoncer quelques règles importantes pour ce marathon:
*Le respect entre participants (même si les réponses sont fausses)
*La numérotation du problème "résolu" et du nouvel problème à résoudre
*Varier le type des exercices
*Faire appel au théorèmes et/ou règles utilisés pendant la démonstration ( Pour éviter l'ambiguïté et aider les gens à connaitre de nouvelles règles si elle ne connaissait pas déja)
*Spoiler ses réponses
| |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Jeu 02 Sep 2010, 00:44 Jeu 02 Sep 2010, 00:44 | |
| - darkpseudo a écrit:
- Voila je pense : Réponse de l'exercice 3
- Spoiler:
D'abord les nombres sont pair ( facil a prouver en modulo 4 )
ensuite on a x=y=z=0 est une solution :
puis x²-x²y²+y²+z² = 0
x²(y²-1) = y²+z²
donc y²-1/z²+1
or ceci reviendrait à dire que y-1/z²+1 et y+1/z²+1
je pense que dès lors la réponse est clair
Je crois qu'il y a quelque chose qui marche pas dans ce qui est en rouge  il se peut que je me trompe  sinon , voilà ma solution pour l'exercice 3:- Spoiler:
EDIT : dans le 2ème cas que j'ai traité , ça nous mène à une infinité de solutions apparemment nn?  une petite confirmation/intervention me fera un grand plaisir  P.S:Je vois qu'il y a encore un problème( N°2) proposé par darkpseudo ... j'essayerai avec 
Dernière édition par tarask le Jeu 02 Sep 2010, 02:18, édité 1 fois | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Jeu 02 Sep 2010, 01:31 Jeu 02 Sep 2010, 01:31 | |
| Heu oui tu a raison , c'est just une faute voulais écrire autre chose , mais ça change rien ^^ | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Jeu 02 Sep 2010, 16:54 Jeu 02 Sep 2010, 16:54 | |
| Salut tout le monde  j'ai trouvé une solution pour l'exercice N°2 , qui est presque la même que j'ai faite pour l'exercice N°3 je donnerai un indice en spoiler : - Spoiler:
on a d'après l'équation du départ x^3 divise (y^4)-1 alors il existe un k de Z tel que (y^4)-1=k.x^3 et on procède de la même manière que dans l'exercice précédent  sauf erreur biensur !
Et pour que le jeu ne s'arrête pas je vous propose cet exercice soit n de N : (2^n) +1 peut-il être un cube ? Bonne continuation  P.S: désolé si l'exercice est un peu facile mais c'est tout ce que j'ai trouvé  | |
|
  | |
soukki
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 31
Localisation : Casa
Date d'inscription : 22/03/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Jeu 02 Sep 2010, 17:28 Jeu 02 Sep 2010, 17:28 | |
| Gros n'importe quoi, Désolé..
Dernière édition par soukki le Jeu 02 Sep 2010, 17:33, édité 1 fois | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Jeu 02 Sep 2010, 17:30 Jeu 02 Sep 2010, 17:30 | |
| - soukki a écrit:
- Spoiler:
Gros n'importe quoi ....
ta réponse est fausse  (matdirhach mni 9ellet swab  c'est le ramadan  ) Gentiment !
Dernière édition par tarask le Jeu 02 Sep 2010, 17:34, édité 1 fois | |
|
  | |
soukki
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 31
Localisation : Casa
Date d'inscription : 22/03/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Jeu 02 Sep 2010, 17:32 Jeu 02 Sep 2010, 17:32 | |
| Hahaha..
Tkt maddrthach mnnk 9allt swab..Ramdan,oui..
DESOLEE!!! | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Jeu 02 Sep 2010, 18:02 Jeu 02 Sep 2010, 18:02 | |
| Bonjour à vous. Voici une Solution du problème 4: - Spoiler:
 Dans N plutôt et non dans Z.
Problème N°5 :Montrer que 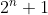 est premier 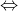 n est une puissance de 2. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Jeu 02 Sep 2010, 18:23 Jeu 02 Sep 2010, 18:23 | |
| - Othmaann a écrit:
Problème N°5 :
Montrer que 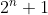 est premier est premier 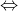 n est une puissance de 2. n est une puissance de 2. Seule => est vraie. <= est fausse. (Cf. la conjecture de Fermat) | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Jeu 02 Sep 2010, 18:54 Jeu 02 Sep 2010, 18:54 | |
| Une réponse après lftour incha2allah  bssa7a ftorkum ! EDIT: comme promis voilà ma solution pour l'exercice N°5- Spoiler:
et pour ceux qui veulent une autre solution pour l'exercice N°4- Spoiler:
Pour Math=life , oui je sais bien qu'il y a une faute dans ma solution  mais ça mérite d'être vue pour identifier l'erreur  et désolé si c'est méchant de ma part haha  Gentiment  En fait c'est Euler qui a donné un contre-exemple pour l'autre implication en 1732 
Dernière édition par tarask le Jeu 02 Sep 2010, 20:04, édité 2 fois | |
|
  | |
Math=life
Maître
 Nombre de messages : 105 Nombre de messages : 105
Age : 33
Date d'inscription : 12/02/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Jeu 02 Sep 2010, 19:49 Jeu 02 Sep 2010, 19:49 | |
| Dijkschneier a érit:- Spoiler:
(Cf. la conjecture de Fermat)
Il a deja répondu a ce problème, pas raison de vous fatiguer tarask, je vous propose ce petit exercice: - Spoiler:
Soit n>1 un entier et p un nombre premier tel que n divise (p-1) et p divise (n^3 -1)
Prouver que (4p-3) est un carré
| |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 | |
  | |
Math=life
Maître
 Nombre de messages : 105 Nombre de messages : 105
Age : 33
Date d'inscription : 12/02/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Ven 03 Sep 2010, 18:52 Ven 03 Sep 2010, 18:52 | |
| Exercice N°6: - Spoiler:
Soit n>1 un entier et p un nombre premier tel que n divise (p-1) et p divise (n^3 -1)
Prouver que (4p-3) est un carré
| |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Ven 03 Sep 2010, 19:45 Ven 03 Sep 2010, 19:45 | |
| Euuh je crois qu'il reste plus que 4 minutes pour que tu postes la solution parce que tu l'as posté hier à 19:49  - Spoiler:
j'avais pensé au Théorème de Wilson et à celui de Fermat , mais en vain. J'aimerai bien voir une solution 
| |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Ven 03 Sep 2010, 19:54 Ven 03 Sep 2010, 19:54 | |
| Voici la soluce : - Spoiler:
Soit k un entier>0 t.q p=nk+1 on a :
p |(n-1)(n²+n+1) => p |n²+n+1 puisque p>n-1
donc :
p| k(n²+n+1) -(n+1)(nk+1)=k-n-1
Il est facile de vérifie que pour n,k>1 on a : |nk+1|>|k-n-1| alors on doit avoir k=n+1 d'où :
4p-3=(2n+1)²
CQFD ..
| |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Ven 03 Sep 2010, 20:54 Ven 03 Sep 2010, 20:54 | |
| - Sylphaen a écrit:
- Voici la soluce :
- Spoiler:
Soit k un entier>0 t.q p=nk+1 on a :
p |(n-1)(n²+n+1) => p |n²+n+1 puisque p>n-1
donc :
p| k(n²+n+1) -(n+1)(nk+1)=k-n-1
Il est facile de vérifie que pour n,k>1 on a : |nk+1|>|k-n-1| alors on doit avoir k=n+1 d'où :
4p-3=(2n+1)²
CQFD ..
Bonsoir Sylphaen  Toute la démarche que t'as faite est juste mais je vois pas pourquoi on aura forcément k=n+1  enfin c'est ce que je crois  | |
|
  | |
M.AlMokhtar
Débutant

 Nombre de messages : 3 Nombre de messages : 3
Age : 30
Localisation : Souk-el-Arba-du-Gharb, Morocco
Date d'inscription : 18/07/2010
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Ven 03 Sep 2010, 21:26 Ven 03 Sep 2010, 21:26 | |
| bon soir si |k-n-1|>=1 on aura |k-n-1|>=|kn+1| ce qui est absurde sylphaen a passé vitement mais c'est clair quand meme  AU plaisir !!! | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  Ven 03 Sep 2010, 23:08 Ven 03 Sep 2010, 23:08 | |
| Problème 7 :
Soit p un nombre premier >2 et n un entier>1 MQ l'équation :
2p+3p=an n'admet pas de solution dans Z | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Marathon de l'arithmétique Sujet: Re: Marathon de l'arithmétique  | |
| |
|
  | |
| | Marathon de l'arithmétique |  |
|
