| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants |
|
| Auteur | Message |
|---|
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 09 Juil 2011, 19:21 Sam 09 Juil 2011, 19:21 | |
| - nmo a écrit:
- Je vais faire une solution pour le problème 107 plus tard, et je vous propose maintenant ces deux problèmes:
Problème 109:
Calculez }) . .
Solution du problème 109:Avec un peu de calcul on obtient que: cos(5a)= 16cos^5(a)-20cos^3(a)+5cos(a) ; avec a appartenant à R On note x=cos(π/5) on obtient l'équation suivante 16x^5-20x^3+5x+1=(x+1)(4x^2-2x-1)^2=0 ce qui implique que: 4x^2-2x-1=0 ALors x_1= (1+√5)4 et x_2=(1-√5)/4 car cos(π/5) >0 Donc cos(π/5)=(1+√5)/4=2cos^2(π/10)-1 Alors cos(π/10)= 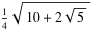 | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 09 Juil 2011, 20:17 Sam 09 Juil 2011, 20:17 | |
| - Mehdi.O a écrit:
- Le problème 109 est classique, ce serait mieux de le changer.
Non, regarde mon post scriptum. - expert_run a écrit:
- nmo a écrit:
- Je vais faire une solution pour le problème 107 plus tard, et je vous propose maintenant ces deux problèmes:
Problème 109:
Calculez }) . .
Solution du problème 109:
Avec un peu de calcul on obtient que: cos(5a)= 16cos^5(a)-20cos^3(a)+5cos(a) ; avec a appartenant à R
On note x=cos(π/5)
on obtient l'équation suivante 16x^5-20x^3+5x+1=(x+1)(4x^2-2x-1)^2=0
ce qui implique que: 4x^2-2x-1=0
ALors x_1= (1+√5)4 et x_2=(1-√5)/4 car cos(π/5) >0
Donc cos(π/5)=(1+√5)/4=2cos^2(π/10)-1
Alors cos(π/10)=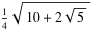 Très bien, je continue donc: On a }=\frac{1}{4}.\sqrt{10+2\sqrt{5}}) . Cela implique que }=\frac{1}{16}.(10+2\sqrt{5})=\frac{1}{8}.(5+\sqrt{5})) soit }}=\frac{8}{5+\sqrt{5}}) . Donc }=\frac{8}{5+\sqrt{5}}) . Ainsi }=\frac{8}{5+\sqrt{5}}-1=\frac{8-5-\sqrt{5}}{5+\sqrt{5}}=\frac{3-\sqrt{5}}{5+\sqrt{5}}=\frac{(3-\sqrt{5})(5-\sqrt{5})}{(5+\sqrt{5})(5-\sqrt{5}}) . Ou encore }\frac{15-3.\sqrt{5}-5.\sqrt{5}+5}{25-5}=\frac{20-8.\sqrt{5}}{20}=\frac{20-8.\sqrt{5}}{20}=1-\frac{8\sqrt{5}}{4.\sqrt{5}.\sqrt{5}}) . Et finalement }=1-\frac{2}{\sqrt{5}}) . Je continue demain, si je trouve du temps. | |
|
  | |
Mehdi.A
Maître
 Nombre de messages : 100 Nombre de messages : 100
Age : 60
Date d'inscription : 07/05/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 09 Juil 2011, 21:01 Sam 09 Juil 2011, 21:01 | |
| D'apreès le theoreme de la calculatrice graduée non scientifiquement programmée on a :
cos(pi/10)=0,95105651629515357211643933337938
Sauf erreur ! | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 | |
  | |
Mehdi.A
Maître
 Nombre de messages : 100 Nombre de messages : 100
Age : 60
Date d'inscription : 07/05/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 09 Juil 2011, 22:13 Sam 09 Juil 2011, 22:13 | |
| OK Merci az360
problème 111 :
Montrer que Si T est une théorie récursivement axiomatisable qui permet de formaliser « suffisamment d'arithmétique », et dont tous les axiomes sont vrais dans N, alors il existe un énoncé G vrai dans N qui n'est pas démontrable dans T
** | |
|
  | |
SarakZit.A
Habitué

 Nombre de messages : 11 Nombre de messages : 11
Age : 57
Localisation : Chine
Date d'inscription : 02/07/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 10 Juil 2011, 22:14 Dim 10 Juil 2011, 22:14 | |
| - Mehdi.A a écrit:
- OK Merci az360
problème 111 :
Montrer que Si T est une théorie récursivement axiomatisable qui permet de formaliser « suffisamment d'arithmétique », et dont tous les axiomes sont vrais dans N, alors il existe un énoncé G vrai dans N qui n'est pas démontrable dans T
** pas mal ! la preuve est disponible dans un de mes écrits (traités d'arithmétique) de 1984. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 10 Juil 2011, 22:41 Dim 10 Juil 2011, 22:41 | |
| - Mehdi.A a écrit:
- OK Merci az360
problème 111 :
Montrer que Si T est une théorie récursivement axiomatisable qui permet de formaliser « suffisamment d'arithmétique », et dont tous les axiomes sont vrais dans N, alors il existe un énoncé G vrai dans N qui n'est pas démontrable dans T
** C'est un théorème d'incomplétude; on peut le déduire directement du théorème de Tarski. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 12 Juil 2011, 20:40 Mar 12 Juil 2011, 20:40 | |
| - nmo a écrit:
- Problème 107:
Soit 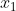 , , 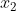 , ... et , ... et 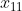 11 nombres rééls. 11 nombres rééls.
Parmi ces rééls, montrez qu'il existe deux distincts 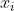 et et 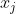 tel que tel que ^2\le\bigg(1-\frac{2}{\sqrt{5}}\bigg)(1+x_i.x_j)^2) . . Voici la solustion que je vous ai promis: On pose: }) , pour tout i compris entre 1 et 11. Les angles 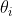 sont compris entre -90° et 90°. Trouver deux indices i et j qui répondent au problème, équivaut à trouver deux indices i et j tel que }-\tan{(\theta_j)})^2\le\bigg(1-\frac{2}{\sqrt{5}}\bigg)(1+\tan{(\theta_i)}.\tan{(\theta_j)})^2) soit }-\tan{(\theta_j)})^2}{(1+\tan{(\theta_i)}.\tan{(\theta_j)})^2}=\bigg(\frac{\tan{(\theta_i)}-\tan{(\theta_j)})^2}{(1+\tan{(\theta_i)}.\tan{(\theta_j)}}\bigg)^2\le1-\frac{2}{\sqrt{5}}) . Ou encore, trouver deux indices i et j, qui sont distincts, qui vérifient }\le1-\frac{2}{\sqrt{5}}) . On procède comme suit: Nous avons donc 11 angles dans un intervalle de longueur 180°. En divisant ce dernier en 10 tiroirs de longueur 18°, on voit que deux angles sont à distance monidre de 18°. C'est à dire qu'il existe deux indices distincts i et j tel que  , ou encore que  . En passant à la tangente, on aboutit à }\le\tan{(\frac{\pi}{10})}) . Cette denière inégalité équivaut à }\le\tan^2{(\frac{\pi}{10})}) . Et en vertu de l'exercice 109 et de mon travail qui suit la réponse de expert_run, on tombe sur: }\le1-\frac{2}{\sqrt{5}}) . CQFD. Sauf erreur. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 13 Juil 2011, 18:40 Mer 13 Juil 2011, 18:40 | |
| - Mehdi.A a écrit:
- problème 111 :
Montrer que Si T est une théorie récursivement axiomatisable qui permet de formaliser « suffisamment d'arithmétique », et dont tous les axiomes sont vrais dans N, alors il existe un énoncé G vrai dans N qui n'est pas démontrable dans T
** D'emblée, j'ai cru que c'est du charabia. Mais après une recherche dans Internet, il s'est avéré qu'il s'agit du premier théorème d'incomplétude de Godel. Et je ne vois pas quel est l'intérêt de proposer un exercice qui dépasse largement ce niveau. Je sais mon cher que tu le sais, voire tu es capable de lui apporter la démonstration. Pour répondre -respecter les règles du jeu-, voici un lien où on expose une preuve: http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_d'incompl%C3%A9tude_de_G%C3%B6del Au plaisir. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 15 Juil 2011, 11:01 Ven 15 Juil 2011, 11:01 | |
| Je propose un nouveau problème:
Problème 112:
Afin de me préparer pour les olympiades internationales, je résous au moins un problème par jour pour garder les théorèmes en tête, mais pas plus de 10 par semaine pour ne pas se fatiguer.
Prouver que si je continue ainsi suffisemment longtemps, il y aura une période continue de jours pendant laquelle j'aurais résolu exactement 21 problèmes.
Bonne chance. | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 15 Juil 2011, 11:19 Ven 15 Juil 2011, 11:19 | |
| deja posté dans le forum .
| |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 15 Juil 2011, 11:27 Ven 15 Juil 2011, 11:27 | |
| - Sporovitch a écrit:
- deja posté dans le forum.
Ce serait gentil de ta part de me donner le lien, car je ne sais plus comment procéder. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 15 Juil 2011, 12:12 Ven 15 Juil 2011, 12:12 | |
| En attente d'une réponse pour le problème 112, je propose un autre problème: Problème 113:Soient 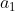 , 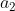 , ... et 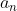 n nombres rééls strictement positifs. Démontrez que }}<\sqrt{\sum_{k=1}^{n}a_k}+1) . Bonne chance. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 15 Juil 2011, 21:56 Ven 15 Juil 2011, 21:56 | |
| - nmo a écrit:
Problème 113:
Soient 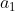 , , 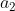 , ... et , ... et 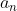 n nombres rééls strictement positifs. n nombres rééls strictement positifs.
Démontrez que }}<\sqrt{\sum_{k=1}^{n}a_k}+1) . .
Bonne chance. Solution 113:On a  on démontre donc cette inégalité par récurrence: pour n=1 on a  ce qui est vrai. Alors on suppose que l'inégalité initiale est vraie; et montrons qu'elle est vraie pour n+1. On note 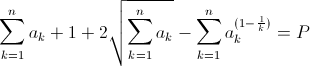 alors démontrons: 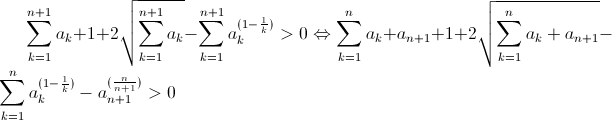 Donc  Dans le cas où 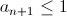 On considère la fonction  Alors pour 0<x=< 1 f'(x)=< 0 donc f est décroissante On déduit donc que: pour 0<x=< 1 ; f(x)>=f(1)=c+1 On posons  On obtient que : 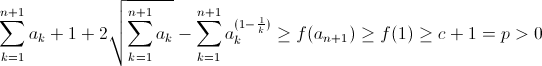 Ce qui assure la conclusion. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 16 Juil 2011, 13:13 Sam 16 Juil 2011, 13:13 | |
| - expert_run a écrit:
- Donc
 Ce que tu avance ici est juste si  . Je pense que tu dois rectifier, ou me convaicre de la validité de ce que tu écris. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 19 Juil 2011, 11:16 Mar 19 Juil 2011, 11:16 | |
| - nmo a écrit:
- expert_run a écrit:
- Donc
 Ce que tu avance ici est juste si  . .
Je pense que tu dois rectifier, ou me convaicre de la validité de ce que tu écris. Alors essaie un contre exemple a_{n+1}=1/2 et n=1 donc a_{n+1}-a_{n+1}^(1/2)=1/2-v(1/2) < 0 C'est pour ca qu'on ne peut pas dire que c est juste pour  . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 21 Juil 2011, 12:05 Jeu 21 Juil 2011, 12:05 | |
| - expert_run a écrit:
- Alors essaie un contre exemple a_{n+1}=1/2 et n=1
donc a_{n+1}-a_{n+1}^(1/2)=1/2-v(1/2) < 0
C'est pour ca qu'on ne peut pas dire que c est juste pour  . . Ce que je veux dire tout simplement que tu as  si et seulement si  . Qu'en penses-tu, maintenant? | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 21 Juil 2011, 12:16 Jeu 21 Juil 2011, 12:16 | |
| Oui c'est ca que j'ai fait. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 21 Juil 2011, 12:38 Jeu 21 Juil 2011, 12:38 | |
| - expert_run a écrit:
- Oui c'est ca que j'ai fait.
D'emblée, je n'ai pas bien compris ce que tu as fait. Je m'excuse. Il reste le problème 112, et je crois avoir trouver une réponse que je vais proposer plus tard. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 21 Juil 2011, 15:09 Jeu 21 Juil 2011, 15:09 | |
| - nmo a écrit:
- Problème 112:
Afin de me préparer pour les olympiades internationales, je résous au moins un problème par jour pour garder les théorèmes en tête, mais pas plus de 10 par semaine pour ne pas se fatiguer.
Prouver que si je continue ainsi suffisemment longtemps, il y aura une période continue de jours pendant laquelle j'aurais résolu exactement 21 problèmes.
Bonne chance. Vous pouvez lire la solution là-bas: http://www.maths-forum.com/principe-tiroirs-exemple-compris-123044.php. (C'est la réponse que j'ai trouvé en tapant les mots-clés du problème dans la barre de recherche de google). Bonne découverte. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 21 Juil 2011, 15:17 Jeu 21 Juil 2011, 15:17 | |
| Je propose un problème qui n'est plus facile: Problème 114:Soient a et b deux réels. Trouver tous les triplets de réels strictement positifs (x,y,z) vérifiant:  . Bonne chance.
Dernière édition par nmo le Ven 22 Juil 2011, 12:48, édité 1 fois | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 22 Juil 2011, 12:33 Ven 22 Juil 2011, 12:33 | |
| En dernier c'est z^2+b^2 ou z^2+x^2 | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 22 Juil 2011, 12:48 Ven 22 Juil 2011, 12:48 | |
| - expert_run a écrit:
- En dernier c'est z^2+b^2 ou z^2+x^2
C'est la première. C'est une faute d'inattention. Je vais éditer. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 22 Juil 2011, 12:50 Ven 22 Juil 2011, 12:50 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 25 Juil 2011, 13:24 Lun 25 Juil 2011, 13:24 | |
| Voici un exercice de plus: Problème 115:Un groupe de personne a visité une exposition de 97 tableaux. On suppose que tous les tableaux ont été vus. Par contre, aucune personne n'a vu tous les tableaux. Démontrez qu'il existe deux personnes 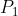 et 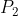 et deux tableaux 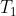 et 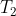 tels que 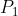 a vu 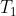 et n'a pas vu 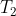 et 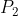 a vu 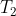 et n'a pas vu 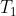 . Bonne chance. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de première (2010-2011) |  |
|
