Préparations aux olympiades de première (2010-2011)

M.Marjani a écrit:

Dijkschneier a écrit:

Solution au problème 5 :
1/ Supposons par l'absurde que l'un des nombres est égal à 1, mettons c.
Alors la première condition devient : ab > 1, et la deuxième : a + b < 1/a + 1/b
La deuxième est alors équivalente à 1 < 1/ab, ou encore à ab < 1.
Contradiction avec le fait que ab > 1.
2/ Supposons par l'absurde que tous les nombres entre a, b et c sont supérieurs (strictement ?) à 1.
Selon l'inégalité de Cauchy-Schwarz, on a a+b+c > 9/(1/a+1/b+1/c). Ainsi, la deuxième condition implique que 1/a + 1/b + 1/c > 3.
Or 1/a, 1/b, 1/c < 1 car a,b et c > 1. De fait 1/a + 1/b + 1/c < 3.
On a bien un discours contradictoire.

PS : on peut supposer par l'absurde dans 2/ que les nombres sont strictement supérieurs à 1 sans perte de généralité car d'après 1/, aucun des nombres ne peut égaler 1.

Et que chacun se sente libre de proposer un nouveau problème.

Pour la deuxiéme, tu n'as montré (peut-étre) qu'un cas parmi deux cas (Selon ma vision), il te faut discuter du cas oû seulement l'un des réels positives a,b,c est strictement positive à 1 : )
Une fois çelà est prouvé par l'absurde, il te reste un seule cas qui est deux réels positives parmi a,b,c est strictement à 1. Ce que je le pense pas étre utile à déduire qu'un réel positive est plus petit que 1..

Pourtant je pense qu'il fallait chercher une autre methode, ou bien reprendre. Pour la methode que j'ai fais, la premiére question n'était qu'un complément de dire que tout est stricte : )

Comment tu interprètes la phrase : "L'un des trois nombres est plus petit que 1." ?
a)
b)
En ce qui me concerne, j'ai considéré que "L'un des trois nombres est plus petit que 1." était équivalente à a).
Il me semble que b) est fausse de toute façon.

Dijkschneier a écrit:

M.Marjani a écrit:

Dijkschneier a écrit:

Solution au problème 5 :
1/ Supposons par l'absurde que l'un des nombres est égal à 1, mettons c.
Alors la première condition devient : ab > 1, et la deuxième : a + b < 1/a + 1/b
La deuxième est alors équivalente à 1 < 1/ab, ou encore à ab < 1.
Contradiction avec le fait que ab > 1.
2/ Supposons par l'absurde que tous les nombres entre a, b et c sont supérieurs (strictement ?) à 1.
Selon l'inégalité de Cauchy-Schwarz, on a a+b+c > 9/(1/a+1/b+1/c). Ainsi, la deuxième condition implique que 1/a + 1/b + 1/c > 3.
Or 1/a, 1/b, 1/c < 1 car a,b et c > 1. De fait 1/a + 1/b + 1/c < 3.
On a bien un discours contradictoire.

PS : on peut supposer par l'absurde dans 2/ que les nombres sont strictement supérieurs à 1 sans perte de généralité car d'après 1/, aucun des nombres ne peut égaler 1.

Et que chacun se sente libre de proposer un nouveau problème.

Pour la deuxiéme, tu n'as montré (peut-étre) qu'un cas parmi deux cas (Selon ma vision), il te faut discuter du cas oû seulement l'un des réels positives a,b,c est strictement positive à 1 : )
Une fois çelà est prouvé par l'absurde, il te reste un seule cas qui est deux réels positives parmi a,b,c est strictement à 1. Ce que je le pense pas étre utile à déduire qu'un réel positive est plus petit que 1..

Pourtant je pense qu'il fallait chercher une autre methode, ou bien reprendre. Pour la methode que j'ai fais, la premiére question n'était qu'un complément de dire que tout est stricte : )

Comment tu interprètes la phrase : "L'un des trois nombres est plus petit que 1." ?
a)
b)
En ce qui me concerne, j'ai considéré que "L'un des trois nombres est plus petit que 1." était équivalente à a).
Il me semble que b) est fausse de toute façon.

Oui, ça peut étre la premiére condition et la deuxiéme en méme temps.. Car ils n'ont pas mentioné qu'il y on a seulement un des 3 trois réels positives est strictement moins que 1 : )

La condition a+b+c < 1/a + 1/b + 1/c serait trés utile à mon avis : )

M.Marjani a écrit:

Oui, ça peut étre la premiére condition et la deuxiéme en méme temps..

a) ou b) <=> a). J'ai prouvé a).

M.Marjani a écrit:

Car ils n'ont pas mentioné qu'il y on a seulement un des 3 trois réels positives est strictement moins que 1 : )

Ils ? Merci de proposer des problèmes à la hauteur et pour lesquels on est sûr de la solution.
b) est sûrement fausse.

Il suffit maintenant de passer à un nouveau problème.
Je n'ai pas de problème à proposer.

Dijkschneier a écrit:

M.Marjani a écrit:

Oui, ça peut étre la premiére condition et la deuxiéme en méme temps..

a) ou b) <=> a). J'ai prouvé a).

M.Marjani a écrit:

Car ils n'ont pas mentioné qu'il y on a seulement un des 3 trois réels positives est strictement moins que 1 : )

Ils ? Merci de proposer des problèmes à la hauteur et pour lesquels on est sûr de la solution.
b) est sûrement fausse.

Il suffit maintenant de passer à un nouveau problème.
Je n'ai pas de problème à proposer.

Ewa chouf nta.. C'est toi le moderateur du sujet. J'ai dis ma point de vue : ) En plus je t'ai suivi dans ta methode, c'était pas une question que je n'ai pas mémoriser l'exercise, mais ce n'est pas moi qui crée l'exercise je l'ai collé tel qu'il.
C'est toi qui a mis: a) ou b) ; moi j'ai dis qu'ils peuvent étre les deux en méme temps ^^
Le tout est pour la deuxiéme question. Enfin ta solution pour le deuxiéme question n'est pas compléte..

M.Marjani a écrit:

moi j'ai dis qu'ils peuvent étre les deux en méme temps ^^

Non, ils ne le peuvent pas.
a) et b) <=> b). Mais b) est sûrement fausse.

EDIT : M.Marjani a peut-être raison : b) est peut-être vraie.
EDIT 2 : définitivement, M.Marjani a raison. b) est aussi vraie.
Preuve que b) est vraie :
Par l'absurde, supposons que 0 < a,b < 1 < c.
La deuxième condition est équivalente à (1/c - c + (a+b)(1-1/ab) >= 0).
Or (ab < 1), donc (-1/ab < -1), donc (1-1/ab < 0), donc (a+b)(1-1/ab) < 0, donc (1/c - c >= 1/c - c + (a+b)(1-1/ab)), et par conséquent, 1/c - c >= 0.
Cela est clairement faux étant donné que c > 1.

Dijkschneier a écrit:

M.Marjani a écrit:

moi j'ai dis qu'ils peuvent étre les deux en méme temps ^^

Non, ils ne le peuvent pas.
a) et b) <=> b). Mais b) est sûrement fausse.

EDIT : M.Marjani a peut-être raison : b) est peut-être vraie.
EDIT 2 : définitivement, M.Marjani a raison. b) est aussi vraie.
Preuve que b) est vraie :
Par l'absurde, supposons que 0 < a,b < 1 < c.
La deuxième condition est équivalente à (1/c - c + (a+b)(1-1/ab) >= 0).
Or (ab < 1), donc (-1/ab < -1), donc (1-1/ab < 0), donc (a+b)(1-1/ab) < 0, donc (1/c - c >= 1/c - c + (a+b)(1-1/ab)), et par conséquent, 1/c - c >= 0.
Cela est clairement faux étant donné que c > 1.

Ha.

Voiçi ma Solution 5:

1/ On suppose par exemple que a=1 alors (b*c > 1 ET b+c < 1/b + 1/c) alors 1/c + 1/b < 1/b + 1/c ce qui est absurde.. car LHS=RHS.
2/ On va utiliser:
On a: [On factorise avec ab-1 qui est plus grand que 1/c -1]
(1)
Donc on est sur trois cas:
Si: (a,b,c) > 1 implique que a > 1/a , b > 1/b et c > 1/c alors a+b+c > 1/a + 1/b + 1/c qui est contradictoire avec la deuxiéme condition.
Si: (a,b)>1>c on aura 1/c -1 > 0 alors par (1) Il faut que 1/b + 1/a - 1/c -1<0 Ce qui est vrai car 1/b + 1/a <2 mais 1/c + 1 > 2.
Si: (a,b)<1<c alors 1/b + 1/c > 2 et 1/c + 1 < 2 alors 1/b + 1/a - 1/c - 1 > 0 , donc selon (1) il faut que 1/c - 1 < 0 ce qui est juste car c>1.

PS: Dans chaque factorisation du départ, on trouvera que au moin l'un des trois réels positives est moin que 1.

---------------------------------------------------------------------------------------------------------------------------------

Et c'est fini. Merçi : )

On continue notre jeu avec un autre probléme du méme genre, une remarque trés jolie qu'on peut tous tomber sur elle sans conscience.. : )

Probléme 6:



PS: Moi aussi je vais réflichir à l'exercise : )

M.Marjani a écrit:

Probléme 6:

PS: Moi aussi je vais réflichir à l'exercise : )

D'emblée, on remarque que le couple (0,0) est solution du système (2) et que ce couple ne vérifie pas le système (1).
Donc les deux systèmes n'ont pas les mêmes ensembles de solutions.
Pour se justifier la réponse, je pense que pour multiplier ou diviser par un x ou un y, il faut qu'il soient non nuls.
J'attends une confirmation.

nmo a écrit:

D'emblée, on remarque que le couple (0,0) est solution du système (2) et que ce couple ne vérifie pas le système (1).
Donc les deux systèmes n'ont pas les mêmes ensembles de solutions.
Pour se justifier la réponse, je pense que pour multiplier ou diviser par un x ou un y, il faut qu'il soient non nuls.
J'attends une confirmation.

Cela est faux que pour la dévision, d'ailleur multiplier par un 0 les deux cotés çelà reste toujours juste 0*t=0*y <=> 0=0. Il te faut plus de détailles.

EDIT: Puisque nmo est approché à la réponse finale, c'est à lui de proposer l'exercise suivant.

M.Marjani a écrit:

nmo a écrit:

D'emblée, on remarque que le couple (0,0) est solution du système (2) et que ce couple ne vérifie pas le système (1).
Donc les deux systèmes n'ont pas les mêmes ensembles de solutions.
Pour se justifier la réponse, je pense que pour multiplier ou diviser par un x ou un y, il faut qu'il soient non nuls.
J'attends une confirmation.

Cela est faux que pour la dévision, d'ailleur multiplier par un 0 les deux cotés çelà reste toujours juste 0*t=0*y <=> 0=0. Il te faut plus de détailles.
EDIT: Puisque nmo est approché à la réponse finale, c'est à lui de proposer l'exercise suivant.

Je pense qu'il s'agit d'une solution en utilisant l'implication.
C'est pour cela qu'il faut s'assurer que les résultats trouvés appartiennent ou non à l'ensemble des solutions.
(une faute récurrente souvent commise).

nmo a écrit:

M.Marjani a écrit:

nmo a écrit:

D'emblée, on remarque que le couple (0,0) est solution du système (2) et que ce couple ne vérifie pas le système (1).
Donc les deux systèmes n'ont pas les mêmes ensembles de solutions.
Pour se justifier la réponse, je pense que pour multiplier ou diviser par un x ou un y, il faut qu'il soient non nuls.
J'attends une confirmation.

Cela est faux que pour la dévision, d'ailleur multiplier par un 0 les deux cotés çelà reste toujours juste 0*t=0*y <=> 0=0. Il te faut plus de détailles.
EDIT: Puisque nmo est approché à la réponse finale, c'est à lui de proposer l'exercise suivant.

Je pense qu'il s'agit d'une solution en utilisant l'implication.
C'est pour cela qu'il faut s'assurer que les résultats trouvés appartiennent ou non à l'ensemble des solutions.
(une faute récurrente souvent commise).

Oui, biensure. J'ai pas d'exercise à proposer. A toi : )
Let go Hard..

Je crois qu'il est malheureux que ce marathon tombe à l'eau.
Merci de ne pas manquer de le ravitailler en problèmes divers et variés.
Par exemple :
Problème 7:
Montrer que .

Dijkschneier a écrit:

Je crois qu'il est malheureux que ce marathon tombe à l'eau.
Merci de ne pas manquer de le ravitailler en problèmes divers et variés.
Par exemple :
Problème :
Montrer que .

T'as raison ! Le problème c'est que le nombre de membres intéressés par les olympiades diminue de plus en plus Je sais pas pourquoi ! La difficulté des exercices ? je crois pas ....
Bon courage M.Marjani , Dijkschneier , nmo et louis, keep it up

M.Marjani a écrit:

nmo a écrit:

M.Marjani a écrit:

nmo a écrit:

D'emblée, on remarque que le couple (0,0) est solution du système (2) et que ce couple ne vérifie pas le système (1).
Donc les deux systèmes n'ont pas les mêmes ensembles de solutions.
Pour se justifier la réponse, je pense que pour multiplier ou diviser par un x ou un y, il faut qu'il soient non nuls.
J'attends une confirmation.

Cela est faux que pour la dévision, d'ailleur multiplier par un 0 les deux cotés çelà reste toujours juste 0*t=0*y <=> 0=0. Il te faut plus de détailles.
EDIT: Puisque nmo est approché à la réponse finale, c'est à lui de proposer l'exercise suivant.

Je pense qu'il s'agit d'une solution en utilisant l'implication.
C'est pour cela qu'il faut s'assurer que les résultats trouvés appartiennent ou non à l'ensemble des solutions.
(une faute récurrente souvent commise).

Oui, biensure. J'ai pas d'exercise à proposer. A toi : )
Let go Hard..

Ce n'est pas là le problème,bien au contraire!C'est juste qu'on essai de ce concentrer sur les exercices des premiers cours afin de partir d'un bon pas!

Dijkschneier a écrit:

Je crois qu'il est malheureux que ce marathon tombe à l'eau.
Merci de ne pas manquer de le ravitailler en problèmes divers et variés.
Par exemple :
Problème :
Montrer que .

Solution:

L'inégalité

Spoiler:

Ce qui est clairement juste.

M.Marjani a écrit:

L'inégalité

Spoiler:

Ce qui est clairement juste.

En quoi c'est clair ?! C'est bien ce qu'il faut démontrer !

@Dijkschneier:

Spoiler:

Dijkschneier a écrit:

Je crois qu'il est malheureux que ce marathon tombe à l'eau.
Merci de ne pas manquer de le ravitailler en problèmes divers et variés.
Par exemple :
Problème :
Montrer que .

Tant que plusieurs amateurs de maths sont présents, ce marathon ne tombera jamais à l'eau.
Voilà la solution de l'exercice:
Selon l'inégalité de bernoulli, pour tout n un entier naturel et pour tout réel positif .
En particulier, si ,
L'inégalité devient .
Donc .
Ainsi .
(le terme est toujours positifs).
Soit .==>(1)
D'un autre côté, on a .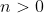
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .==>(2)
De 1 et 2, on déduit que quelquesoit n un entier non nul .
CQFD.
P.S: pour perfectionner la réponse, voici le lien guidant à la démonstration de l'inégalité de bernoulli:
https://mathsmaroc.jeun.fr/seconde-tronc-commun-f6/preparations-aux-olympiades-de-tronc-commun-2009-2010-t14310-315.htm.

La géométrie, elle aussi est l'un des piliers des mathématiques.
De cette optique, je vous propose le premier exercice de géométrie:
Problème 8:
Dans un parallélogramme ABCD, on se donne M sur [AB] et N sur [BC] de sorte que les segments [AM] et [CN] aient des longueurs égales non nulles. (AN) et (CM) se coupent en Q.
Montrer que [DQ) est la bissectrice de ADC.
Bonne chance.
P.S: J'attends une confirmation de la part de Dijkschneier à propos de ma solution pour son exercice.

Oui nmo, l'inégalité de Bernouilli est en effet la clé de l'exercice. Tu aurais pu écrire une solution plus directe, néanmoins. Il reste que ta solution est juste.

nmo a écrit:

La géométrie, elle aussi est l'un des piliers des mathématiques.
De cette optique, je vous propose le premier exercice de géométrie:
Problème 8:
Dans un parallélogramme ABCD, on se donne M sur [AB] et N sur [BC] de
sorte que les segments [AM] et [CN] aient des longueurs égales non
nulles. (AN) et (CM) se coupent en Q.
Montrer que [DQ) est la bissectrice de ADC.

Solution au problème 8 :
Les triangles AMQ et NQC sont clairement isométriques. Par conséquent, CQ=AQ. Cela suffit pour dire que les deux triangles ADQ et ACQ sont isométriques. Par conséquent, AD=DC. CQFD.

Dijkschneier a écrit:

nmo a écrit:

La géométrie, elle aussi est l'un des piliers des mathématiques.
De cette optique, je vous propose le premier exercice de géométrie:
Problème 8:
Dans un parallélogramme ABCD, on se donne M sur [AB] et N sur [BC] de
sorte que les segments [AM] et [CN] aient des longueurs égales non
nulles. (AN) et (CM) se coupent en Q.
Montrer que [DQ) est la bissectrice de ADC.

Solution au problème 8 :
Les triangles AMQ et NQC sont clairement isométriques. Par conséquent, CQ=AQ. Cela suffit pour dire que les deux triangles ADQ et ACQ sont isométriques. Par conséquent, AD=DC. CQFD.

Peux-tu le prouver?
Personellement, je n'ai pas encore abordé cet exercice. Il me parait facile quand même.
Si je ne trouve pas de solution demain matin, je présenterai la solution et un autre exercice.

nmo a écrit:

Dijkschneier a écrit:

nmo a écrit:

La géométrie, elle aussi est l'un des piliers des mathématiques.
De cette optique, je vous propose le premier exercice de géométrie:
Problème 8:
Dans un parallélogramme ABCD, on se donne M sur [AB] et N sur [BC] de
sorte que les segments [AM] et [CN] aient des longueurs égales non
nulles. (AN) et (CM) se coupent en Q.
Montrer que [DQ) est la bissectrice de ADC.

Solution au problème 8 :
Les triangles AMQ et NQC sont clairement isométriques. Par conséquent, CQ=AQ. Cela suffit pour dire que les deux triangles ADQ et ACQ sont isométriques. Par conséquent, AD=DC. CQFD.

Peux-tu le prouver?
Personellement, je n'ai pas encore abordé cet exercice. Il me parait facile quand même.
Si je ne trouve pas de solution demain matin, je présenterai la solution et un autre exercice.

Il est en effet très facile, en cela qu'il se limite à une application des notions acquises sur les triangles isométriques.

Pour prouver que AMQ et NQC sont isométriques, on utilise la deuxième caractérisation des triangles isométriques : deux triangles sont isométriques lorsqu'ils ont un côté de même longueur compris entre deux angles de même mesure.
Ici, on a AM=NC, et l'angle AMQ étant égal à l'angle NQC, alors les angles entre lesquels les deux côtés AM et NC sont compris dans les deux triangles sont respectivement égaux.

Dijkschneier a écrit:

nmo a écrit:

Dijkschneier a écrit:

nmo a écrit:

La géométrie, elle aussi est l'un des piliers des mathématiques.
De cette optique, je vous propose le premier exercice de géométrie:
Problème 8:
Dans un parallélogramme ABCD, on se donne M sur [AB] et N sur [BC] de
sorte que les segments [AM] et [CN] aient des longueurs égales non
nulles. (AN) et (CM) se coupent en Q.
Montrer que [DQ) est la bissectrice de ADC.

Solution au problème 8 :
Les triangles AMQ et NQC sont clairement isométriques. Par conséquent, CQ=AQ. Cela suffit pour dire que les deux triangles ADQ et ACQ sont isométriques. Par conséquent, AD=DC. CQFD.

Peux-tu le prouver?
Personellement, je n'ai pas encore abordé cet exercice. Il me parait facile quand même.
Si je ne trouve pas de solution demain matin, je présenterai la solution et un autre exercice.

Il est en effet très facile, en cela qu'il se limite à une application des notions acquises sur les triangles isométriques.

Pour prouver que AMQ et NQC sont isométriques, on utilise la deuxième caractérisation des triangles isométriques : deux triangles sont isométriques lorsqu'ils ont un côté de même longueur compris entre deux angles de même mesure.
Ici, on a AM=NC, et l'angle AMQ étant égal à l'angle NQC, alors les angles entre lesquels les deux côtés AM et NC sont compris dans les deux triangles sont respectivement égaux.

Je ne pense pas, il se peut qu'on a 45° et 5° dans un triangle et 40° et 10°.
Ainsi, ta solution est fausse.
Bon, une solution dans mon prochain message.

Alain Larroche a écrit:

.

P.S: je n'ai pas le temps de l'écrire en utilisant le clavier.

Problème 9:
Démontrez que est un nombre rationnel.
Bonne chance.