| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants |
|
| Auteur | Message |
|---|
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 05 Oct 2010, 21:18 Mar 05 Oct 2010, 21:18 | |
| - nmo a écrit:
- Dijkschneier a écrit:
Pour prouver que AMQ et NQC sont isométriques, on utilise la deuxième caractérisation des triangles isométriques : deux triangles sont isométriques lorsqu'ils ont un côté de même longueur compris entre deux angles de même mesure.
Ici, on a AM=NC, et l'angle AMQ étant égal à l'angle NQC, alors les angles entre lesquels les deux côtés AM et NC sont compris dans les deux triangles sont respectivement égaux.
Je ne pense pas, il se peut qu'on a 45° et 5° dans un triangle et 40° et 10°.
Ainsi, ta solution est fausse.
Bon, une solution dans mon prochain message. J'ai dit n'importe quoi, désolé. Merci d'avoir rectifié. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 11 Oct 2010, 13:40 Lun 11 Oct 2010, 13:40 | |
| - nmo a écrit:
- Problème 9:
Démontrez que ^3}+\sqrt{(4-\sqrt{15})^3}}{\sqrt{(6+\sqrt{35})^3}-\sqrt{(6-\sqrt{35})^3}}) est un nombre rationnel. est un nombre rationnel.
Bonne chance. C'est bon je l'ai raisolu, pour continuer ce bon marathon. Tout est à remarquer que (Va)^3+(Vb)^3=(Va+Vb)(a+b-ab) Et (Va)^3-(Vb)^3=(Va-Vb)(a+b+V(ab)) Et aprés: (Va+Vb)/(Vx-Vy)=(Vx+Vy)(Va+Vb)/(x-y) Ce qui reste que des calculs... A la fin j'ai trouvé que ce nombre est égale à: 7/13 Alors c'est un rationel ! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 12 Oct 2010, 09:49 Mar 12 Oct 2010, 09:49 | |
| Le résultat trouvé par M.Marjani est juste. Je propose un nouveau problème: Problème 10:Soit f la fonction numérique de la variable x définie par: =\sqrt{a^2+x^2}+\sqrt{(b-x)^2+c^2}) . Tel que a, b, et c sont des rééls positifs. Trouvez la valeur inférieure de la fonction f. Bonne chance. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 12 Oct 2010, 12:44 Mar 12 Oct 2010, 12:44 | |
| Solution au problème 10 :
L'inégalité de Minkowski affirme que f(x) >= sqrt((a+c)²+b²).
Avec égalité ssi x=ab/(a+c).
sqrt((a+c)²+b²) est donc le minimum de la fonction. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 12 Oct 2010, 21:12 Mar 12 Oct 2010, 21:12 | |
| - Dijkschneier a écrit:
- Solution au problème 10 :
L'inégalité de Minkowski affirme que f(x) >= sqrt((a+c)²+b²).
Avec égalité ssi x=ab/(a+c).
sqrt((a+c)²+b²) est donc le minimum de la fonction. Tu peux me montrer les étapes que t'as suivi en utilisant Minkowski? ------------------------------------------------------------------------------------------------------------------------ Voiçi une autre methode: On sait que: (ab-ax-xc)² >= 0 d'ou (a²+x²)((b-x)²+c²)-(ac+bc-x²)²>=0 <=> x²-bx+V((a²+x²)((b-x)²+c²)>=ac <=> 2x²-2bx+2V((a²+x²)((b-x)²+c²)>=2ac <=> a²+c²+x²+( b²+x²-2bx)+2V((a²+x²)((b-x)²+c²)>= a²+c²+2ac+ b²<=> (a²+x²)+2V((a²+x²)((b-x)²+c²)+((b-x)²+c²) >= ((a+c)²+b²) <=> (V(a²+x²)+V((b-x)²+c²))² >= V((a+c)²+b²) <=> V(a²+x²)+V((b-x)²+c²)>=V((a+c)²+b²)Donc V((a+c)²+b²) est la valeur infernal de f(x). | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 13 Oct 2010, 12:57 Mer 13 Oct 2010, 12:57 | |
| Problème 11 :Soit (D) une droite du plan, et soient E et F deux points distincts de la droite. Trouver le ou les emplacements du point M de (D) qui minimisent la somme ME+MF. Problème 12 : Soient (D) et (Delta) deux droites parallèles du plan, et soient E et F deux points distincts des deux droites, et tels que E soit du côté de (D), et F de celui de (Delta). Trouver le ou les emplacements des deux points K et H de (D) et (Delta) respectivement qui minimisent la somme EK+KH+HF et tels que (KH) soit perpendiculaire aux deux droites (D) et (Delta). | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 18 Oct 2010, 21:41 Lun 18 Oct 2010, 21:41 | |
| N'oublions pas ces questions.
Le problème 11 est un classique à connaître par cœur. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 19 Oct 2010, 14:40 Mar 19 Oct 2010, 14:40 | |
| - M.Marjani a écrit:
- Dijkschneier a écrit:
- Solution au problème 10 :
L'inégalité de Minkowski affirme que f(x) >= sqrt((a+c)²+b²).
Avec égalité ssi x=ab/(a+c).
sqrt((a+c)²+b²) est donc le minimum de la fonction. Tu peux me montrer les étapes que t'as suivi en utilisant Minkowski?
------------------------------------------------------------------------------------------------------------------------
Voiçi une autre methode:
On sait que: (ab-ax-xc)² >= 0 d'ou (a²+x²)((b-x)²+c²)-(ac+bc-x²)²>=0
<=> x²-bx+V((a²+x²)((b-x)²+c²)>=ac
<=> 2x²-2bx+2V((a²+x²)((b-x)²+c²)>=2ac
<=> a²+c²+x²+(b²+x²-2bx)+2V((a²+x²)((b-x)²+c²)>=a²+c²+2ac+b²
<=> (a²+x²)+2V((a²+x²)((b-x)²+c²)+((b-x)²+c²) >= ((a+c)²+b²)
<=> (V(a²+x²)+V((b-x)²+c²))² >= V((a+c)²+b²)
<=> V(a²+x²)+V((b-x)²+c²)>=V((a+c)²+b²)
Donc V((a+c)²+b²) est la valeur infernal de f(x). Ta methode est bonne si on te demande la démonstration de ce qui est en rouge. Sinon, comment tu sait sue c'est la valeur inférieure de f(x). - Dijkschneier a écrit:
- N'oublions pas ces questions.
Le problème 11 est un classique à connaître par cœur. Ce n'est qu'une question de manque de temps. Demain, si j'ai le temps, je posterai les solutions complètes. J'aime aussi savoir le principe de l'inégalité de Minkowski, et comment tu l'as utilisé. En plus je vais rédiger une autre solution du problème 10, proposé par DIMA DIMA, pour votre plaisir. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 20 Oct 2010, 13:08 Mer 20 Oct 2010, 13:08 | |
| - nmo a écrit:
- J'aime aussi savoir le principe de l'inégalité de Minkowski, et comment tu l'as utilisé.
L'utilisation de l'inégalité est immédiate. Il suffit de connaître son énoncé. Google-le et tu auras l'énoncé. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 20 Oct 2010, 15:27 Mer 20 Oct 2010, 15:27 | |
| - nmo a écrit:
- Problème 10:
Soit f la fonction numérique de la variable x définie par:
=\sqrt{a^2+x^2}+\sqrt{(b-x)^2+c^2}) . .
Tel que a, b, et c sont des rééls positifs.
Trouvez la valeur inférieure de la fonction f.
Bonne chance. Je commece par vous présenter la solution que je vous ai prévu, et bonne découverte: Dans le plan euclédien, on considère un repère orthonormé ) . On considère ensuite les points ) , ) , et ) tel que x est un réel variant. On a  et ^2+c^2}) . Et par suite =AM+BM) . Soit ) l'image de A par rapport à l'axe des abcisses. Puisque ) , il s'ensuit que  . Ainsi =MA'+BM) . Et on sait que  , tel que 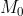 est l'intersection de la droite (A'B) et l'axe des abcisses. Donc  . Donc \ge A'B) . Et puisque ^2}) . Alors \ge \sqrt{b^2+(a+c)^2}) . (L'équation =\sqrt{b^2+(a+c)^2}) a une solution). Ainsi la valeur inférieure de f(x) est sans conteste ^2}) . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 20 Oct 2010, 15:35 Mer 20 Oct 2010, 15:35 | |
| - Dijkschneier a écrit:
- Problème 11 :
Soit (D) une droite du plan, et soient E et F deux points distincts de la droite.
Trouver le ou les emplacements du point M de (D) qui minimisent la somme ME+MF. Voici la solution mon cher, Soit E' l'image de E par la reflexion d'axe (D) et soit M un point de la droite (D). On a  car D est la médiatrice du segment [EE']. Selon l'inégalité triangulaire, appliqué dans le triangle E'MF, on a  . Donc  . L'égalité aura lieu si et seulement si M appartient à la droite (E'F). Synthèse: L'emplacement du point M de (D) qui minimise la somme ME+MF est celui de l'intersection de (E'F) avec la droite (D) et que E' soit la symétrique de E par rapport à (D). | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 20 Oct 2010, 16:12 Mer 20 Oct 2010, 16:12 | |
| - Dijkschneier a écrit:
- Problème 12 :

Soient (D) et (Delta) deux droites parallèles du plan, et soient E et F deux points distincts des deux droites, et tels que E soit du côté de (D), et F de celui de (Delta).
Trouver le ou les emplacements des deux points K et H de (D) et (Delta) respectivement qui minimisent la somme EK+KH+HF et tels que (KH) soit perpendiculaire aux deux droites (D) et (Delta). Je réponds: Soit E' l'unique point du plan, pour que le quadrilatère EE'HK soit un parallélogramme. Ainsi  et  . Or, on a, comme l'exercice précédant,  . Avec égalité si H est l'intersection de la droite (  ) et (E'F). Donc  . Donc  . Synthèse: l'emplacement des deux points K et H de (D) et (  ) respectivement qui minimise la somme EK+KH+HF et tels que (KH) soit perpendiculaire aux deux droites (D) et (  ) est l'intersection de (E'F) avec la droite (  ) notée H, la construction de K est ensuite facile, tel que E' est l'image de E par la translation de vecteur  . Sauf erreur. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 20 Oct 2010, 16:55 Mer 20 Oct 2010, 16:55 | |
| Je ne dispose pas d'un grand nombre d'exercices d'olympiade. Je vous propose un exercice qui me tourmente la tête depuis des mois: Problème 13:Soit  ,  , et 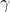 des réels strictement positifs tel que  . Démontrez que  . Bonne chance.
Dernière édition par nmo le Ven 22 Oct 2010, 11:05, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 20 Oct 2010, 20:21 Mer 20 Oct 2010, 20:21 | |
| Très bien nmo. Tes solutions aux deux problèmes précédents sont justes.
| |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 20 Oct 2010, 21:20 Mer 20 Oct 2010, 21:20 | |
| Solution au problème 13 :L'inégalité est équivalente à : ) On a d'après l'inégalité de Cauchy-Schwarz : (\sum%20_{cyc}%20\alpha%20^3%20\gamma%20^2)%20\geq%20(\sum%20_{cyc%20}\alpha^3%20\beta%20\gamma)^2%20=%20(\alpha%20\beta%20\gamma%20(\alpha^2%20+%20\beta^2%20+%20\gamma^2))^2) . Tout en ayant d'après l'inégalité du réordonnement :  . On en conclut facilement l'inégalité désirée. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 20 Oct 2010, 22:02 Mer 20 Oct 2010, 22:02 | |
| Un problème plutôt facile pour les olympiades mais quand même intéressant, car donnant une propriété équivalente à la bijection : Problème 14 :Soient E et F deux ensembles et f une application définie sur E et à valeurs dans F. Montrer que : f bijective <=> %20:%20F%20-%20f(X)%20=%20f(E-X)) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 23 Oct 2010, 18:37 Sam 23 Oct 2010, 18:37 | |
| - Dijkschneier a écrit:
- Solution au problème 13 :
L'inégalité est équivalente à : )
On a d'après l'inégalité de Cauchy-Schwarz : (\sum%20_{cyc}%20\alpha%20^3%20\gamma%20^2)%20\geq%20(\sum%20_{cyc%20}\alpha^3%20\beta%20\gamma)^2%20=%20(\alpha%20\beta%20\gamma%20(\alpha^2%20+%20\beta^2%20+%20\gamma^2))^2) . .
Tout en ayant d'après l'inégalité du réordonnement :  . .
On en conclut facilement l'inégalité désirée. Google ne donne aucun résultat à propos de l'inégalité de réordonnement. Peux-tu me donner son principe? - Dijkschneier a écrit:
- Un problème plutôt facile pour les olympiades mais quand même intéressant, car donnant une propriété équivalente à la bijection :
Problème 14 :
Soient E et F deux ensembles et f une application définie sur E et à valeurs dans F.
Montrer que : f bijective <=> %20:%20F%20-%20f(X)%20=%20f(E-X)) On n'a pas encore entammé cette leçon, puis-je le changer? et on reviendra à lui plus tard. (Aussi le problème 13 que j'ai présenté était simple, et je veux réctifié la faute de poster un exercie de telle difficulté) Merci pour ta compréhension. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 23 Oct 2010, 19:05 Sam 23 Oct 2010, 19:05 | |
| Puisque je n'ai pas assez de temps, excuse-moi de ne pas pouvoir t'attendre: (J'admet que tu n'es pas contre ce que j'ai proposé) Problème 15:
Résolvez en 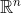 ce système:  . Bonne chance. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Oct 2010, 16:09 Dim 24 Oct 2010, 16:09 | |
| Solution au problème 15 :En sommant toutes les inégalités à la fois, on obtient :  . Or, on a ^2}{n}) d'après l'inégalité de Cauchy-Schwarz, donc ^2}{n}) , ce qui veut dire ^2%20-%20n\sum_{i=1}^{n}%20x_i%20+%20n^2%20\leq%200) . Mais cela n'est pas possible, car Delta < 0, et ainsi ^2%20-%20n\sum_{i=1}^{n}%20x_i%20+%20n^2%20 > %200) Synthèse : Synthèse : Le système n'a pas de solution dans 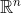 . | |
|
  | |
soumitous
Maître
 Nombre de messages : 218 Nombre de messages : 218
Age : 30
Localisation : Rabat
Date d'inscription : 29/11/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Oct 2010, 18:53 Dim 24 Oct 2010, 18:53 | |
| Bonsoir,
Alors je traine depuis des semaines à résoudre UN SEUL problème au complet (ou c'est la moitié du problème ou c'est rien) mais en vain!!! Sérieux je veux juste comprendre comment vous connaissez toutes ces inégalités ( Cauchy Schwarz etc etc) . Et est-ce que les exercices des olympiades sont comme ça?? :O Et puis comment ça vous tombent sur la tête de faire telle ou telle méthode ? (à force de travailler?)
Je voudrais vraiment participé avec vous mais votre niveau dépasse de LOOOOOOOIN le mien :p | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 24 Oct 2010, 20:47 Dim 24 Oct 2010, 20:47 | |
| Problème 16 :
Soient x,y et z des réels strictement positifs, tels que 1/x + 1/y + 1/z = 1.
Montrez que (x-1)(y-1)(z-1) >= 8.
EDIT : problème remplacé.
Dernière édition par Dijkschneier le Lun 25 Oct 2010, 21:00, édité 2 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 25 Oct 2010, 00:17 Lun 25 Oct 2010, 00:17 | |
| - nmo a écrit:
- Puisque je n'ai pas assez de temps, excuse-moi de ne pas pouvoir t'attendre:
(J'admet que tu n'es pas contre ce que j'ai proposé)
Problème 15:
Résolvez en 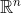 ce système: ce système:
 . .
Bonne chance. C'est assez façile je pense, quand méme voiçi ma réponse: En sommant les inégalité des donées on obtient: Cygma{i=1 --> n}(x_i ²) +n = (Cygma{i=1 --> n}(x_i) Or: x_1 ² + 1 >= 2*x_1 ==> (1) x_2 ² + 1 >= 2*x_2 ==> (2) . . . x_n ² + 1 >= 2*x_n ==> (n) En sommant: (1) , (2) et ... et (n): Cygma{i=1 --> n}(x_i ²) +n >= 2*(Cygma{i=1 --> n}(x_i) Mais 2*(Cygma{i=1 --> n}(x_i) > (Cygma{i=1 --> n}(x_i) , donc S=l'ensemble vide. PS: J'ai également résolu le probléme de Dijkchneier, c'est aussi façile à résoudre mais une bonne propriéte ! | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 27 Oct 2010, 15:54 Mer 27 Oct 2010, 15:54 | |
| Et donc ? Problème courant : - Citation :
- Problème 16 :
Soient x,y et z des réels strictement positifs, tels que 1/x + 1/y + 1/z = 1.
Montrez que (x-1)(y-1)(z-1) >= 8. Problème 17 :Soit ABC un triangle et D le pied de la bissectrice intérieure de l'angle A. Montrez que : AD² = AB.AC - BD.CD. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 27 Oct 2010, 16:45 Mer 27 Oct 2010, 16:45 | |
| - Dijkschneier a écrit:
- Problème 16 :
Soient x,y et z des réels strictement positifs, tels que 1/x + 1/y + 1/z = 1.
Montrez que (x-1)(y-1)(z-1) >= 8.
EDIT : problème remplacé. On a (x-1)(y-1)(z-1)>=8. Equivaut à dire que (xy-x-y+1)(z-1)>=8. Et puis à xyz-xy-xz-zy+x+y+z-1>=8. Ensuite à xyz-(xy+yz+zx)+(x+y+z)>=9. Or, on a 1/x +1/y +1/z =1. Donc, en multipliant par xyz, xy+yz+zx=xyz. Ainsi xyz-xyz+x+y+z>=9. Donc x+y+z>=9. Démontrons ce résultat. On sait par ailleurs que selon IAG, on a (x+y+z)(1/x +1/y +1/z)>=9. En vertu de 1/x +1/y +1/z=1, Il s'ensuit que x+y+z>=9. CQFD. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 27 Oct 2010, 16:47 Mer 27 Oct 2010, 16:47 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de première (2010-2011) |  |
|
