| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants |
|
| Auteur | Message |
|---|
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 27 Oct 2010, 18:55 Mer 27 Oct 2010, 18:55 | |
| Problème 18 :
Soit P un polynôme à coefficients entiers. On suppose qu’il existe trois entiers a, b et c tels que
P(a) = b, P(b) = c et P(c) = a. Montrer que a = b = c.
Problème 19 :
Soit P un polynôme de degré 2008 tel que P(k)=1/k pour tout k appartenant à {1,2,3,...,2009}. Calculer P(0). | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 27 Oct 2010, 19:05 Mer 27 Oct 2010, 19:05 | |
| - Dijkschneier a écrit:
- Problème 17 :
Soit ABC un triangle et D le pied de la bissectrice intérieure de l'angle A.
Montrez que : AD² = AB.AC - BD.CD. Es-tu sûr de l'exercice? Puisque je n'aurai pas peut-être de temps dans la prochaine semaine, je propose moi aussi cet exercice: Problème 20: - Dijkschneier a écrit:

Soient (D) et (Delta) deux droites parallèles du plan, et soient E et F deux points distincts des deux droites, et tels que E soit du côté de (D), et F de celui de (Delta). Trouver le ou les emplacements des deux points K et H de (D) et (Delta) respectivement qui minimisent la somme EK²+KH²+HF² et tels que (KH) soit perpendiculaire aux deux droites (D) et (Delta). Bonne chance. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 27 Oct 2010, 19:14 Mer 27 Oct 2010, 19:14 | |
|
Dernière édition par Mehdi.O le Lun 01 Nov 2010, 16:34, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 27 Oct 2010, 19:18 Mer 27 Oct 2010, 19:18 | |
| - Mehdi.O a écrit:
- Voici un exo :
xyz=1
Calculer S= (x+1)/(xy+x+1)+(y+1)/(y+yz+1)+(z+1)/(z+xz+1)
Un autre exo :
x+1/y=y+1/z=z+1/x
Montrez que |xyz|=1
(x;y;z)€IR^3 Deux classiques tirés de DIMA DIMA et dont les solutions y figurent. Au plaisir. (Je me rapelle le deuxième exercice des olympiades de la troisième année du collège qui n'est autre que ton premier exercice, la solution est présentée aussi dans le forum des troncs communs, tu n'as qu'à chercher) | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 27 Oct 2010, 19:26 Mer 27 Oct 2010, 19:26 | |
|
Dernière édition par Mehdi.O le Lun 01 Nov 2010, 16:34, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mer 27 Oct 2010, 19:32 Mer 27 Oct 2010, 19:32 | |
| Ceci est un marathon. Merci de ne pas l'inonder de 1000 problèmes alors que les problèmes précédents n'ont pas encore été résolus.
Et nom de dieu, numérotez les problèmes !
@Mehdi.O : Merci de numéroter tes deux derniers problèmes ou bien de les supprimer.
@nmo : Je ne propose jamais de problème sans l'avoir étudié. Il est correct. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 28 Oct 2010, 17:01 Jeu 28 Oct 2010, 17:01 | |
| - Dijkschneier a écrit:
- Problème 17 :
Soit ABC un triangle et D le pied de la bissectrice intérieure de l'angle A.
Montrez que : AD² = AB.AC - BD.CD. Selon le théorèmer des bissectrices intérieures, on a ^2\bigg)) . ==>(1) Et aussi  . Donc  . Donc  . D'où  . Donc ^2) . Donc ^2=\frac{BD.DC}{AB.AC}) . En remplaçant dans 1, on aura ) . Donc  . Enfin  . CQFD. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 28 Oct 2010, 17:29 Jeu 28 Oct 2010, 17:29 | |
| | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Jeu 28 Oct 2010, 18:57 Jeu 28 Oct 2010, 18:57 | |
| - Dijkschneier a écrit:
- Ceci est un marathon. Merci de ne pas l'inonder de 1000 problèmes alors que les problèmes précédents n'ont pas encore été résolus.
Et nom de dieu, numérotez les problèmes !
@Mehdi.O : Merci de numéroter tes deux derniers problèmes ou bien de les supprimer.
@nmo : Je ne propose jamais de problème sans l'avoir étudié. Il est correct. Je vous prie de m'excuser  | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 30 Oct 2010, 21:28 Sam 30 Oct 2010, 21:28 | |
| Problème 21 :
x1,x2,x3 sont des racines du polynôme P(x) = x^3+9x+6
Calculez : 1/x1+1/x2+1/x3
Dernière édition par Mehdi.O le Dim 31 Oct 2010, 16:20, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 31 Oct 2010, 11:51 Dim 31 Oct 2010, 11:51 | |
| - Mehdi.O a écrit:
- Problème 18 :
x1,x2,x3 sont des racines du polynôme P(x) = x^3+9x+6
Calculez : 1/x1+1/x2+1/x3
En fait c'est le problème numéro 21. Essaie de rectifier. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 31 Oct 2010, 12:16 Dim 31 Oct 2010, 12:16 | |
| - Dijkschneier a écrit:
- Problème 18 :
Soit P un polynôme à coefficients entiers. On suppose qu’il existe trois entiers a, b et c tels que
P(a) = b, P(b) = c et P(c) = a. Montrer que a = b = c. Soit P un polynôme tel que =k_{n}x^{n}+k_{n-1}x^{n-1}+k_{n-2}x^{n-2}+...+k_{1}x+k_{0}) et avec 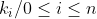 des entiers naturels. On a P(a)=b, P(b)=c et P(c)=a. Donc en sommant P(a)+P(b)à+P(c)=a+b+c. Donc 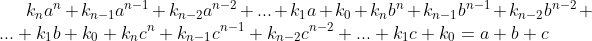 . Donc +k_{n-1}(a^{n-1}+b^{n-1}+c^{n-1})+k_{n-2}(a^{n-2}+b^{n-2}+c^{n-2})+...+k_{1}(a+b+c)+3k_{0}=a+b+c) . Donc 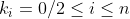 , 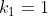 , et 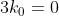 . Et ainsi 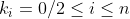 , 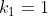 , et 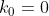 . Donc =0.x^{n}+0.x^{n-1}+0.x^{n-2}+...+1.x+0) . Donc =x) . D'où P(a)=a, P(b)=b et P(c)=c. Donc a=b ,c=b , et a=c. Par conséquent a=b=c. CQFD. Sauf erreur. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 31 Oct 2010, 13:39 Dim 31 Oct 2010, 13:39 | |
| - nmo a écrit:
- Dijkschneier a écrit:
- Problème 18 :
Soit P un polynôme à coefficients entiers. On suppose qu’il existe trois entiers a, b et c tels que
P(a) = b, P(b) = c et P(c) = a. Montrer que a = b = c. Soit P un polynôme tel que =k_{n}x^{n}+k_{n-1}x^{n-1}+k_{n-2}x^{n-2}+...+k_{1}x+k_{0}) et avec et avec 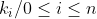 des entiers naturels. des entiers naturels.
On a P(a)=b, P(b)=c et P(c)=a.
Donc en sommant P(a)+P(b)à+P(c)=a+b+c.
Donc 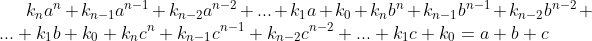 . .
Donc +k_{n-1}(a^{n-1}+b^{n-1}+c^{n-1})+k_{n-2}(a^{n-2}+b^{n-2}+c^{n-2})+...+k_{1}(a+b+c)+3k_{0}=a+b+c) . .
Donc 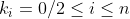 , , 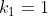 , et , et 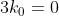 . .
Et ainsi 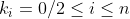 , , 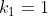 , et , et 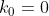 . .
Donc =0.x^{n}+0.x^{n-1}+0.x^{n-2}+...+1.x+0) . .
Donc =x) . .
D'où P(a)=a, P(b)=b et P(c)=c.
Donc a=b ,c=b , et a=c.
Par conséquent a=b=c.
CQFD.
Sauf erreur. L'entier qui est au données, ne veux dire pas qu'il appartient à IN, mais plutot à IZ (Entier relatifs). Tu peux m'expliquer ton passage? De: +k_{n-1}(a^{n-1}+b^{n-1}+c^{n-1})+k_{n-2}(a^{n-2}+b^{n-2}+c^{n-2})+...+k_{1}(a+b+c)+3k_{0}=a+b+c) à :  ET 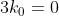 | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 31 Oct 2010, 14:43 Dim 31 Oct 2010, 14:43 | |
| | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 31 Oct 2010, 14:47 Dim 31 Oct 2010, 14:47 | |
| - nmo a écrit:
- Dijkschneier a écrit:
- Problème 17 :
Soit ABC un triangle et D le pied de la bissectrice intérieure de l'angle A.
Montrez que : AD² = AB.AC - BD.CD. Selon le théorèmer des bissectrices intérieures, on a ^2\bigg)) . ==>(1) . ==>(1)
Merci de prouver cette relation car on ne voit pas d'où ça peut venir. Le théorème classique de la bissectrice nous permet de dire que : BD/DC = AB/AC. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 | |
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 31 Oct 2010, 16:57 Dim 31 Oct 2010, 16:57 | |
| Problème 22 : ET abc =1
Dernière édition par Mehdi.O le Mer 17 Nov 2010, 14:26, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 31 Oct 2010, 17:28 Dim 31 Oct 2010, 17:28 | |
| @Mehdi.O : et tes messages précédents au sujet desquels je t'ai fait une remarque, tu vas les supprimer ? | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 31 Oct 2010, 17:39 Dim 31 Oct 2010, 17:39 | |
| Comment supprimer un message? | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 31 Oct 2010, 17:47 Dim 31 Oct 2010, 17:47 | |
| - Mehdi.O a écrit:
- Comment supprimer un message?
Avant de participer, il faut lire ces conditions: - Citation :
- Comme l'évolution de l'âge est irrémédiable, et que le marathon consacré à la préparation des olympiades de seconde touche à sa fin, j'aimerais, en restant dans la même lancée, proposer d'entamer un nouveau marathon qui cette fois-ci sera conçu pour préparer les olympiades de première.
Un peu à la manière de tous les marathons, celui-ci aurait des règles qui ne sortent pas du commun :
- Dans l'idéal, chaque participant ayant donné une solution à un précédent problème doit se charger de proposer un nouveau problème. Si quelqu'un qui répond à un problème n'a pas de nouveau problème à proposer, qu'il l'indique clairement ! D'autres s'en chargeront, si possible.
- Numéroter clairement les problèmes, et citer le numéro du problème dans la solution que l'on en donne.
- Ne pas poster de solutions incomplètes et par conséquent, ne pas attendre de confirmation pour reproposer un nouveau problème.
- Favoriser l'entente et la bonne humeur. Tu doit édité tes deux derniers message oû tu as postulé de nouveau problémes. Il y a dejà deux problémes non resolu. Maniére de les conservé, et les postulé au bonnes moments. (Voir ce qui est en bleu) | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 31 Oct 2010, 18:53 Dim 31 Oct 2010, 18:53 | |
| D'accord veuillez m'excuser ! | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 31 Oct 2010, 22:24 Dim 31 Oct 2010, 22:24 | |
| - Mehdi.O a écrit:
- D'accord veuillez m'excuser !
Tu dis que tu t'excuses mais tu ne t'appliques pas. As-tu supprimé tes messages ? Pour supprimer un message, il faut les éditer et les vider de leur contenu (ne laisser qu'un point). | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 01 Nov 2010, 17:25 Lun 01 Nov 2010, 17:25 | |
| - Dijkschneier a écrit:
- nmo a écrit:
- Dijkschneier a écrit:
- Problème 17 :
Soit ABC un triangle et D le pied de la bissectrice intérieure de l'angle A.
Montrez que : AD² = AB.AC - BD.CD. Selon le théorèmer des bissectrices intérieures, on a ^2\bigg)) . ==>(1) . ==>(1)
Merci de prouver cette relation car on ne voit pas d'où ça peut venir.
Le théorème classique de la bissectrice nous permet de dire que : BD/DC = AB/AC. Voilà le lien pour la solution: https://mathsmaroc.jeun.fr/seconde-tronc-commun-f6/bissectrice-d-un-angle-t13210.htm. Bonne découverte. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 01 Nov 2010, 17:30 Lun 01 Nov 2010, 17:30 | |
| - Dijkschneier a écrit:
- nmo a écrit:
Donc +k_{n-1}(a^{n-1}+b^{n-1}+c^{n-1})+k_{n-2}(a^{n-2}+b^{n-2}+c^{n-2})+...+k_{1}(a+b+c)+3k_{0}=a+b+c) . .
Donc 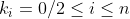 , , 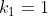 , et , et 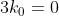 . .
Et ainsi 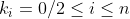 , , 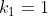 , et , et 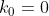 . .
Non ! Ce n'est pas une égalité polynomiale !! C'est quoi donc à ton avis? Si on traite chaque cas séparément, on se ramène à  . Et puis P(a)=0, P(b)=0, et P(c)=0. Ainsi on trouve que a=b=c=0. J'attends ton avis. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 01 Nov 2010, 17:43 Lun 01 Nov 2010, 17:43 | |
| - Mehdi.O a écrit:
- Problème 22 :
 C'est faux, prends a=b=c=1/2. Rapelle-toi de ces paroles: - Dijkschneier a écrit:
- Ceci est un marathon. Merci de ne pas l'inonder de 1000 problèmes alors que les problèmes précédents n'ont pas encore été résolus.
Il reste encore un tas de problèmes sans solutions confirmés, les voici: - Dijkschneier a écrit:
- Problème 14 :
Soient E et F deux ensembles et f une application définie sur E et à valeurs dans F.
Montrer que : f bijective <=> %20:%20F%20-%20f(X)%20=%20f(E-X)) - Dijkschneier a écrit:
- Problème 18 :
Soit P un polynôme à coefficients entiers. On suppose qu’il existe trois entiers a, b et c tels que
P(a) = b, P(b) = c et P(c) = a. Montrer que a = b = c.
Problème 19 :
Soit P un polynôme de degré 2008 tel que P(k)=1/k pour tout k appartenant à {1,2,3,...,2009}. Calculer P(0). - nmo a écrit:
- Problème 20:
- Dijkschneier a écrit:

Soient (D) et (Delta) deux droites parallèles du plan, et soient E et F deux points distincts des deux droites, et tels que E soit du côté de (D), et F de celui de (Delta). Trouver le ou les emplacements des deux points K et H de (D) et (Delta) respectivement qui minimisent la somme EK²+KH²+HF² et tels que (KH) soit perpendiculaire aux deux droites (D) et (Delta).
Bonne chance. Veille à ne pas proposer un autre exercice, avant que ceux-ci ne soient pas encore résolus Cela nuit à la présentation du sujet qui se voit maintenant en ruine. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de première (2010-2011) |  |
|
