| | Préparations aux olympiades du première (2011-2012) |  |
|
+6nmo boubou math Driss Ach Siba aymas Ahmed Taha (bis) 10 participants |
|
| Auteur | Message |
|---|
Driss Ach
Maître
 Nombre de messages : 117 Nombre de messages : 117
Age : 29
Date d'inscription : 29/10/2011
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 15:56 Mer 08 Fév 2012, 15:56 | |
| Probléme 13:On se donne deux réel strictement positifs a et b tel que : 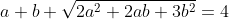 Prouver que : 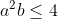 . | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 15:57 Mer 08 Fév 2012, 15:57 | |
| - Siba a écrit:
- V48 = 3.8 à peu près, et c'est pas un entier naturel ...
- Spoiler:
| |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 16:52 Mer 08 Fév 2012, 16:52 | |
| - Spoiler:
donc on peut ajoute aussi x=-V48
| |
|
  | |
Siba
Maître

 Nombre de messages : 143 Nombre de messages : 143
Date d'inscription : 12/12/2011
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 17:17 Mer 08 Fév 2012, 17:17 | |
| Oui,
Sinon pour le 1, j'ai trouvé S = 2013 - (1/3)^2009 , c'est aussi correct ? | |
|
  | |
Siba
Maître

 Nombre de messages : 143 Nombre de messages : 143
Date d'inscription : 12/12/2011
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 17:31 Mer 08 Fév 2012, 17:31 | |
| Qui a fait 6 et 12 ?
Pour 6 on trouve que x^a + y^a - z ^a = x^b + y^b - z^b
Je sais pas si ca conclut la solution... | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 18:25 Mer 08 Fév 2012, 18:25 | |
|
Dernière édition par aymas le Mer 08 Fév 2012, 20:16, édité 3 fois | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 18:38 Mer 08 Fév 2012, 18:38 | |
| Pour le 6 - Spoiler:
Par symétrie,on peut supposer que a>=b, et soit m un entier naturel tel que a=b+m On a ainsi : .z^{m}\Leftrightarrow&space;x^{b}.x^{m}+y^{b}.y^{m}-x^{b}.z^{m}-y^{b}.z^{m}\Leftrightarrow&space;x^{b}(x^{m}-z^{m})+y^{b}(y^{m}-z^{m})=0) d'une autre part : x,y et z sont positifs ainsi une des égalité donné nous suffit pour conclure que : +y^{b}(y^{m}-z^{m})&space;\leq&space;0) Mais d’après la dernière équivalence il nous vient : =0&space;\:&space;\:&space;\:&space;\:&space;et\:&space;\:&space;\:&space;\:&space;y^{b}(y^{m}-z^{m})=&space;0&space;\Rightarrow&space;x^{m}-z^{m}=0&space;\:&space;\:&space;\:&space;\:&space;et&space;\:&space;\:&space;\:&space;y^{m}-z^{m}=0&space;\:&space;\:&space;(x,y>0)\Rightarrow&space;x^{m}=y^{m}=z^{m}\Rightarrow&space;\frac{x^m}{z^m}=\frac{y^m}{z^m}=1\Rightarrow&space;m=0&space;\Rightarrow&space;a=b) dans les derniere implications , il faut aussi traiter le cas ou x=y=z ,ce cas est trivial facile à traiter . sauf erreur...
Amicalement
Dernière édition par boubou math le Mer 08 Fév 2012, 19:19, édité 5 fois | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 18:44 Mer 08 Fév 2012, 18:44 | |
| - aymas a écrit:
- Spoiler:
SAUF ERREUR!!!! On ne peut pas supposer l'existence d'un tel k car on a pas a multiple b et puis x,y et sont des réels et non pas seulement dans IN il faut que tu révise ta solution !!! | |
|
  | |
Siba
Maître

 Nombre de messages : 143 Nombre de messages : 143
Date d'inscription : 12/12/2011
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 19:59 Mer 08 Fév 2012, 19:59 | |
| Oui, en plus l'avant dernère ligne est fausse, on peut pas conclure que x^k +1 = = ... = 1
4 + 6 = 10
ca ne veut pas dire que 4 x 1 + 6 x 1 = 10 x 1 et puis c'est tout, par exemple on a :
4 x 2 + 6 x 2 = 10 x 2 ...
| |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Mer 08 Fév 2012, 20:07 Mer 08 Fév 2012, 20:07 | |
| ah vraiment merci pour ta remarque j'ai pas fais attention
j'ai voulu écrire a=b+k je vais le corrigé | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Jeu 09 Fév 2012, 00:39 Jeu 09 Fév 2012, 00:39 | |
| Pour le 12 On sait bien que parmi les triangles qui ont le même périmètre , le triangle équilatérale a la surface maximal . soit A'B'C' un triangle équilatérale qui a le même périmètre que ABC et notons s' sa surface. on a ainsi 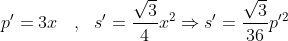 (tel que x est la longueur des cotés du triangle) mais on a s=<s' , ce qui permet de conclure . | |
|
  | |
Siba
Maître

 Nombre de messages : 143 Nombre de messages : 143
Date d'inscription : 12/12/2011
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Jeu 09 Fév 2012, 10:25 Jeu 09 Fév 2012, 10:25 | |
| Vu que personne ne poste de problème , je vous propose celui-ci assez facile:
Problème 14:
Montrer que:
S = 1/4 xsqrt(P x (P-2a)(P-2c)(P-2b))
Dans un triangle de surface S, de perimetre P, et de cotés a , b et c.
Dernière édition par Siba le Jeu 09 Fév 2012, 14:35, édité 1 fois | |
|
  | |
Siba
Maître

 Nombre de messages : 143 Nombre de messages : 143
Date d'inscription : 12/12/2011
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Jeu 09 Fév 2012, 10:53 Jeu 09 Fév 2012, 10:53 | |
| Pour le 13:
Après le calcul pour résoudre l'equation 1, j'ai trouvé le système suivant:
(a+4)x(V2)(b+2) = 20
a = (V2)(b+2)- 4
Après le calcul des valeurs, ca nous mène directement au résultat.
Et pour se rassurer, on peut faire un raisonnement par raisonnement par contraposé, ce qui confirme le résultat.
PS: J'ai pas écrit toute ma solution car j'ai du mal à rédiger les signes de maths sur pc . | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Jeu 09 Fév 2012, 11:15 Jeu 09 Fév 2012, 11:15 | |
| - Siba a écrit:
- Vu que personne ne poste de problème , je vous propose celui-ci assez facile:
Problème 14:
Montrer que:
S = 1/4 xsqrt(P x (P-a)(P-c)(P-b))
Dans un triangle de surface S, de perimetre P, et de cotés a , b et c. je pense que la question est fausse  la formule de héron est : \left&space;(&space;\frac{P}{2}-b&space;\right&space;)\left&space;(&space;\frac{P}{2}-c&space;\right&space;)}\neq&space;\frac{1}{4}\sqrt{P(P-a)(P-b)(P-c)}) | |
|
  | |
Siba
Maître

 Nombre de messages : 143 Nombre de messages : 143
Date d'inscription : 12/12/2011
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Jeu 09 Fév 2012, 14:36 Jeu 09 Fév 2012, 14:36 | |
| J'avais juste fait un peu de changement pour poser la question, sinon voici la démonstration en utilisant al-kashi et la surface d'un triangle...
S = a.c.sinB /2
= ((a.c)/2) xV(1 - cos^2 B)
= ((a.c)/2) xV(1- cos B)(1 + cos B)
= ((a.c)/2) xV(1 - (a^2 + c^2 - b^2)/(2ac))(1 + (a^2 + c^2 - b^2)/(2ac))
= ((a.c)/2) xV( 2ac - a^2 - c^2 + b^2 / 2ac ) ( 2 ac + a^2 + c^2 - b^2 / 2ac)
= 1/2 xV( 1/2 ( 2ac - a^2 - c^2 + b^2) 1/2 (2 ac + a^2 + c^2 - b^2)
= 1/4 xV(b^2 -(a-c)^2)((a+c)^2 - b^2)
= 1/4 xV(b-a+c)(b+a-c)(a+c-b)(a+c+b)
S = 1/4 xV(P x (P-2a)(P-2c)(P-2b)) | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 | |
  | |
Siba
Maître

 Nombre de messages : 143 Nombre de messages : 143
Date d'inscription : 12/12/2011
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Jeu 09 Fév 2012, 18:57 Jeu 09 Fév 2012, 18:57 | |
| On calcule:
X = 1/V(a^2 + 1) - 1/2 + 1/V(b^ + 1) - 1/2 + 1/V(c^2 + 1) -1/2
X = [(2 - V(a^2 + 1)) / 2V(a^2 + 1)] +[(2 - V(b^2 + 1)) / 2V(b^2 + 1)] +[(2 - V(c^2 + 1)) / 2V(c^2 + 1)]
La, il suffit de montrer que 2 - V(a^2 + 1) et 2 - V(b^2 +1) et 2 - V(c^2 +1) sont négatifs.
Prenons a:
2 - V(a^2 + 1) < 0 <==> a > V3
Or,
On sait que si a + b + c = abc , alors la valeur minimal est V3 , parce que:
3m < m^3 ==> m > V3 (ou m est la valeur min)
Il en est de meme pour b et c.
Donc:
2 - V(a^2 + 1) et 2 - V(b^2 +1) et 2 - V(c^2 +1) sont tous négatifs.
Alors:
1/V(a^2 + 1) + 1/V(b^ + 1) + 1/V(c^2 + 1) < 3/2
Sauf erreur !
PS: "<" ca veut dire inférieur ou égal "=<". | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Jeu 09 Fév 2012, 19:46 Jeu 09 Fév 2012, 19:46 | |
| pas forcement on sait que d'apres IAG la valeur minimale de a+b+c=3V3
on suppose que c=<b=<a donc c=<V3 et V3=<a alors la minimalité des variables n'est pas satisfais | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Jeu 09 Fév 2012, 19:56 Jeu 09 Fév 2012, 19:56 | |
| Siba je vais édité l' exo . j'ai commis une faute de frappe. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Jeu 09 Fév 2012, 20:02 Jeu 09 Fév 2012, 20:02 | |
| - aymas a écrit:
- Problème 15:
 L'inégalité à démontré est érronée sinon, pourquoi faire apparaître 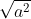 au lieu d'écrire directement a. Je pense que la nouvelle inégalité est sans doute 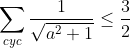 . Il suffit de faire la substition }) , }) , }) . Où \in) [ 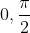 [ et 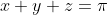 . On a donc 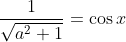 , et cycliquement. Et puis, l'inégalité à démontrer devient }\le\frac{3}{2}) . Ce qui est une application directe de l'inégalité de la convexité (la fonction cosinus étant concave sur [ 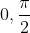 [). CQFD. Sauf erreur. | |
|
  | |
Siba
Maître

 Nombre de messages : 143 Nombre de messages : 143
Date d'inscription : 12/12/2011
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Jeu 09 Fév 2012, 20:06 Jeu 09 Fév 2012, 20:06 | |
| non, c'est faux ce que tu dis:
V3 =< c =< b =< a , on a le cas d'egalité quand a b et c prennent la valeur V3...
tu peux pas dire c =< V3 ... | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Jeu 09 Fév 2012, 20:34 Jeu 09 Fév 2012, 20:34 | |
| peut tu rediger ta demonstration si c'est possible je voudrai egalement la connaitre | |
|
  | |
Siba
Maître

 Nombre de messages : 143 Nombre de messages : 143
Date d'inscription : 12/12/2011
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Jeu 09 Fév 2012, 20:53 Jeu 09 Fév 2012, 20:53 | |
| - aymas a écrit:
- peut tu rediger ta demonstration si c'est possible je voudrai egalement la connaitre
regarde page 3 .. c'est déja fait. Puis , y a nmo qui a utilisé une autre méthode plus simple. | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 | |
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  Jeu 09 Fév 2012, 22:31 Jeu 09 Fév 2012, 22:31 | |
| Pour le 12eme exo j'ai utilisé une methode differente - Spoiler:
[img]http://latex.codecogs.com/gif.latex?En&space;%5C&space;utilisant&space;%5C&space;la&space;%5C&space;tranformation&space;%5C&space;de&space;%5C&space;ravi&space;%5C&space;on&space;%5C&space;a:&space;%5C%5C&space;x=%5Cfrac%7Bb+c-a%7D%7B2%7D&space;%5C&space;y=%5Cfrac%7Ba-b+c%7D%7B2%7D&space;%5C&space;z=%5Cfrac%7Ba+b-c%7D%7B2%7D&space;%5C%5C&space;donc&space;%5C&space;%5Cfrac%7BP%7D%7B2%7D=x+y+z%5C%5C&space;Et&space;%5C&space;d%27apres&space;%5C&space;la&space;%5C&space;formule&space;%5C&space;de&space;%5C&space;h%C3%A9ron&space;%5C&space;on&space;%5C&space;a:%5C%5C&space;S=%5Csqrt%7Bp%28p-a%29%28p-b%29%28p-c%29%7D%5C%5C&space;%5CLeftrightarrow&space;S=%5Csqrt%7Bxyz%28x+y+z%29%7D%5C%5C&space;ainsi&space;%5C&space;l%27in%C3%A9galit%C3%A9&space;%5C&space;est&space;%5C&space;equivalent&space;%5C&space;%C3%A0&space;%5C%5C&space;%5Csqrt%7Bxyz%28x+y+z%29%7D%5Cleq&space;%5Cfrac%7B%5Csqrt%7B3%7D%7D%7B36%7D%5Ctimes&space;4%28x+y+z%29%5E%7B2%7D&space;%5C%5C&space;%5CLeftrightarrow&space;%5Csqrt%7Bxyz%28x+y+z%29%7D%5Cleq&space;%5Cfrac%7B%5Csqrt%7B3%7D%7D%7B9%7D%28x+y+z%29%5E%7B2%7D%5C%5C&space;%5CLeftrightarrow&space;xyz%28x+y+z%29%5Cleq&space;%5Cfrac%7B1%7D%7B27%7D%28x+y+z%29%5E%7B4%7D%5C%5C&space;%5CLeftrightarrow&space;27xyz%5Cleq&space;%28x+y+z%29%5E%7B3%7D%5C%5C&space;Qui&space;%5C&space;est&space;%5C&space;evidement&space;%5C&space;clair&space;%5C&space;d%27apres&space;%5C&space;IAG&space;%5C&space;on&space;%5C&space;a&space;%5C&space;x+y+z%5Cgeq&space;3%5Csqrt[3]%7Bxyz%7D%5CLeftrightarrow&space;27xyz%5Cleq&space;%28x+y+z%29%5E%7B3%7D%5C%5C&space;CQFD[/img]
AMICALLEMENT  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades du première (2011-2012) Sujet: Re: Préparations aux olympiades du première (2011-2012)  | |
| |
|
  | |
| | Préparations aux olympiades du première (2011-2012) |  |
|
