| | Préparations aux olympiades du première (2011-2012) |  |
|
+6nmo boubou math Driss Ach Siba aymas Ahmed Taha (bis) 10 participants |
|
| Auteur | Message |
|---|
alidos
Expert grade2
 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
| | Sujet: Re: Préparations aux olympiades du première (2011-2012) Mer 22 Fév 2012, 12:22 | |
| l'exercice 4 f (2006) = -3 | |
|
| | |
Driss Ach
Maître
Nombre de messages : 117
Age : 29
Date d'inscription : 29/10/2011
| |
| | |
Ahmed Taha (bis)
Expert grade2
Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
| | Sujet: Re: Préparations aux olympiades du première (2011-2012) Mer 22 Fév 2012, 20:00 | |
| - Driss Ach a écrit:
- Probléme 16:
Soit a un réel strictement positif tel que : 
Montrer que l'équation :  n'admet pas de solution dans R. Solution probléme 16:- Spoiler:
l'équation n'admet pas de solution dans R si  d'où %3C&space;0\Rightarrow&space;a^2%3E&space;8&space;\&space;et\&space;a\in\mathbb{R}^+&space;\&space;donc\&space;a%3E&space;\sqrt{8}) on a \Leftrightarrow&space;a(a^2-6)=6) posent que  donc \leq&space;\sqrt{8}\left&space;(&space;8-6&space;\right&space;)%3C&space;6) c'est faut !!!!
| |
|
| | |
Ahmed Taha (bis)
Expert grade2
Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
| | Sujet: Re: Préparations aux olympiades du première (2011-2012) Mer 22 Fév 2012, 20:15 | |
| Probléme 17:On considère l'équation  où  est un paramètre réel. Déterminer les valeurs de pour lesquelles l'équation admet deux solutions  et telles que :  | |
|
| | |
Driss Ach
Maître
Nombre de messages : 117
Age : 29
Date d'inscription : 29/10/2011
| | Sujet: Re: Préparations aux olympiades du première (2011-2012) Mer 22 Fév 2012, 21:20 | |
| abdelkrim-amine a écrit :
- Spoiler:
Problème 17:On considère l'équation 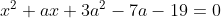 où est un paramètre réel. Déterminer les valeurs de pour lesquelles l'équation admet deux solutions  et telles que :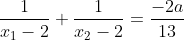 
Solution de problème 17:- Spoiler:
l'équation a admet deux solutions et  si  donc  et 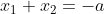 d'ou 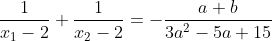 alors  Donc a=4 puisque Delta de  est inférieur de 0
| |
|
| | |
Driss Ach
Maître
Nombre de messages : 117
Age : 29
Date d'inscription : 29/10/2011
| |
| | |
Ahmed Taha (bis)
Expert grade2
Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
| | Sujet: Re: Préparations aux olympiades du première (2011-2012) Mer 22 Fév 2012, 22:25 | |
| | |
|
| | |
Ahmed Taha (bis)
Expert grade2
Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
| | Sujet: Re: Préparations aux olympiades du première (2011-2012) Mer 22 Fév 2012, 22:27 | |
| problème 19:
Soit ABC un triangle d’aire 1 et P le milieu du côté [BC] .
M et N sont deux points de [AB] et [AC] respectivement tels que AM=2MB et CN=2AN .
Les Droites (AP) et (MN) se coupent en un point D .
Trouver l’aire du triangle ADN . | |
|
| | |
alidos
Expert grade2
Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
| | Sujet: Re: Préparations aux olympiades du première (2011-2012) Jeu 23 Fév 2012, 12:47 | |
| abdelkrim stp la solution de l'exo 2 car j'ai une epreuve des olympiades ce vendredi  | |
|
| | |
anas012
Débutant
Nombre de messages : 6
Age : 28
Date d'inscription : 23/02/2012
| | Sujet: Re: Préparations aux olympiades du première (2011-2012) Jeu 23 Fév 2012, 13:25 | |
| salut tous le monde, je veux savoir si il y a un lycée qui a annoncé que les olympiades auront lieu demain (24/02/2012)?????????????? | |
|
| | |
alidos
Expert grade2
Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
| | Sujet: Re: Préparations aux olympiades du première (2011-2012) Jeu 23 Fév 2012, 13:40 | |
| anas wé tous les lycées du maroc  | |
|
| | |
Ahmed Taha (bis)
Expert grade2
Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
| |
| | |
Ahmed Taha (bis)
Expert grade2
Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
| | Sujet: Re: Préparations aux olympiades du première (2011-2012) Jeu 23 Fév 2012, 13:48 | |
| - anas012 a écrit:
- salut tous le monde, je veux savoir si il y a un lycée qui a annoncé que les olympiades auront lieu demain (24/02/2012)??????????????
c demain 24/02/2012 et le 02/03/2012 entrer ici http://www.men.gov.ma/SiteCollectionDocuments/note131110920.pdf | |
|
| | |
alidos
Expert grade2
Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
| | Sujet: Re: Préparations aux olympiades du première (2011-2012) Jeu 23 Fév 2012, 15:33 | |
| merci abdelkrim c trés gentil  | |
|
| | |
alidos
Expert grade2
Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
| | Sujet: Re: Préparations aux olympiades du première (2011-2012) Jeu 23 Fév 2012, 19:29 | |
| abdelkrim j'ai besoin aussi de la solution de l'exo 1 ( j'ai essayé pour simplifiez mais sans resulat )  | |
|
| | |
Ahmed Taha (bis)
Expert grade2
Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
| | Sujet: Re: Préparations aux olympiades du première (2011-2012) Jeu 23 Fév 2012, 20:14 | |
| salut - alidos a écrit:
- abdelkrim j'ai besoin aussi de la solution de l'exo 1 ( j'ai essayé pour simplifiez mais sans resulat )
ok pas de prob mais le 1er exo est déjà résolu ici : - abdelkrim-amine a écrit:
-
- Citation :
- Problème 1:
Calculer :
^2}})
solution problème 1:
- Spoiler:
(cliqué Spoiler: pour voir la solution ) | |
|
| | |
lamperouge
Maître
Nombre de messages : 133
Age : 28
Localisation : Casablanca
Date d'inscription : 13/01/2012
| | Sujet: Re: Préparations aux olympiades du première (2011-2012) Sam 25 Fév 2012, 15:02 | |
| - Citation :
- aymas a écrit:
- Spoiler:
3 pour le troisième
on a pour x=x+3
f(x+5)=f(x+2)f(x+8 )
alors f(x+8 )=f(x+5)/f(x+2)
=f(x-1)
donc f(x)=f(x+9)
c'est a dire f est périodique
f(x+5)/f(x+2)=1/f(x-1) donc je rpropose pour conclure la solution - Spoiler:
on a f(x+  =1/f(x-1) (1) et en mettons x+1 a la place de x dans (1) il s'ensuit que f(x)=1/f(x+9) et en mettons cette fois si x+10 a la place de x dans (1) il s'en suit que 1/f(x+9)=f(x+18) d'ou f(x)=f(x+18) donc f est periodique de periode T=18
| |
|
| | |
amigo-6
Maître
Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
| | Sujet: Re: Préparations aux olympiades du première (2011-2012) Sam 25 Fév 2012, 17:25 | |
| | |
|
| | |
lamperouge
Maître
Nombre de messages : 133
Age : 28
Localisation : Casablanca
Date d'inscription : 13/01/2012
| | Sujet: Re: Préparations aux olympiades du première (2011-2012) Dim 26 Fév 2012, 00:23 | |
| - abdelkrim-amine a écrit:
- Driss Ach a écrit:
- Probléme 16:
Soit a un réel strictement positif tel que :
Montrer que l'équation : n'admet pas de solution dans R.
Solution probléme 16:
- Spoiler:
l'équation n'admet pas de solution dans R si d'où on a posent que donc c'est faut !!!!
Bon je propose cette solution pour l'exo 16 - Spoiler:
on a a^3=6(a+1)
donc il est evident que a est differente de 0
et on a x²+ax+a²-6=0
<=> ax²+a²x+a^3-6a=0
=> ax²+a²x+6=0
apres avoir calculer les descriminants et deduire x en fonction de a on remplace dans la pemiere equation
qui va donner que a=+/-V12
qui tt 2 ne verifient po les proprietes requises pour a
| |
|
| | |
Contenu sponsorisé
| | Sujet: Re: Préparations aux olympiades du première (2011-2012) | |
| |
|
| | |
| | Préparations aux olympiades du première (2011-2012) | |
|
