Préparations aux olympiades de Terminale (2012)

Comme son titre l'indique ce sujet est axé sur la préparation aux olympiades de Terminale, nous tâcherons durant ce topic de proposer des problèmes qui englobent les différents domaines des problèmes qui sont proposés aux olympiades à savoir l'Algèbre, l'Arithmétique, la géométrie, ainsi que la combinatoire.
Les règles de ce jeu ne sortent pas du lot :
- Numéroter les problèmes.
- Indiquer le niveau de difficulté des problèmes proposés ( par des étoiles )
- Ne pas proposer de problèmes arbitrairement, et ne pas en proposer avant de résoudre les autres problèmes.
- Si 48h s'écoulent sans que le problème courant soit résolu, celui qui a proposé le problème doit en donner une solution.
- Celui qui résout un problème en propose directement un autre, ou bien qu'il laisse la main aux autres pour en proposer.
- Mettre les solutions en spoiler.
- Il serait préférable d'utiliser le Latex pour rédiger les solutions.
- En cas d'exercice de géométrie ou de combinatoire, il serait mieux d'attacher à la solution une figure.
- Et bien sûr, tâcher de maintenir le respect et l'ambiance entre forumistes .

Ainsi, je commence par proposer cette EF facile pour inciter les gens à participer .

Problème 1 :
Déterminer toutes les fonctions
tel que :

Classique, 2 substitutions le tue.

n.naoufal a écrit:

Classique, 2 substitutions le tue.

Merci de respecter les règles du jeu.
Soit poster une réponse complète et un nouveau problème, soit ne rien poster .

Ma réponse pour problème 1:

Spoiler:

Problème 2:

Soient a et b deux réels tel que 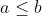et .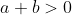

Montrer que quelque-soit les nombres 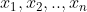de l'intervalle [a,b] on a:

Solution au problème 2:

Spoiler:

Je n'ai pas de problème à proposer actullement, libre à chacun d'en poster.

Problème 3:
Trouver toutes les fonctions réelles et continues g vérifiant : g(g(x))=2g(x)-x

Solution au problème 3:
bonjour,
on pose: g^n(x)=gogo...og(x) n fois
et on considere la suite : Un,x=g^n(x) si n>0,et U0,x=x
il est facile de voir que la suite Un-x est arithmetique (on utilisant la relation initiale)et que :
pour tt entier n on a: Un,x=n(g(x)-x)+x (a)
on suppose mnt qu'il existe b de IR tel que : g(b) est different de b
donc d'apres (a) est par passage de la limite on aura si on remplace x par b: Lim(Un,b)=infini.
or on a: U(n,b)-U(n-1,b)=g(b)-b donc Lim(U(n,b)-U(n-1,b))=g(b)-b
d'une autre part on a : g^n(x)=gog(g^(n-2)(x))=2g^(n-1)(x)-x
d'ou Un,x-Un-1,x=U(n-1,x)-x et par passage a la limite on se trouve absurde (g(b)-b=infini!!!!) par la suite il n existe aucun reel b tel que g(b) est different de b
donc pour tt x g(x)=x...reciproquement l identite est bien une solution de probleme.(sauf erreur)
j'ai pas de probleme a poste

Je pense que c'est faux. Sinon montre rigoureusement que la suite est arithmétique.

pour montrer que la suite est arithemetique il suffit de voir que : Un-Un-1=Un-1-Un-2 (on remplacant x par g^n-2(x)...,si non peux-tu me dire ou est la faute?

Tu as raison U_n-U_{n-1}=U_{n-1}-U_{n-2} mais ça ne veut en aucun cas dire que la suite est arithmétique

et bah si ,c'est une propriete qui caracterise les suite arithnetique tu peux revoir le cour des suites,il suffit de faire une petite sommation de n egalite .

Je répète que non car le terme n'est pas constant ...
C'est pour ça que je demande une démonstration rigoureuse et non il suffit de...

x est constant par rapport a n si on considere une suite parametre c est tout je trouve pas ou est le probleme!tu peux m expliquer ce que tu veux dire d une autre maniere
et pour la demo:
Un-Un-1=Un-1-Un-2
Un-1-Un-2=Un-2-Un-3
........
........
U2-U1=U1-U0
en sommant on aurra Un=Un-1+ U1-U0 !! est donc elle n est pas arithmetique maintenant ??

tu viens de démontrer qu'elle n'est pas arithmétique car ce que tu as écris présuppose que U_1 et U_0 sont constants ...
tout ce que tu auras , c'est g^n(x)-g^{n-1}(x)=g(x)-x.

Je te propose , au lieu de débattre pendant des heures , de rerédiger ta solution plus clairement et beaucoup plus rigoureusement. Car selon moi ce n'est pas la seule erreur.

x est un nombre constant par rapport a n et je sais bien que j ai pas bien rediger ma solution car j avais pas trop de temps en+ vais pas la repete une autre fois c est qd meme claire!!!
et on debat pas ici et je suis desole si ma solution n est pas claire!

Sans t'offenser , ta solution n'est pas juste.
Essaye la fonction qui à x associe x+1 Je ne voulais pas donner de fonctions qui réalise l'énoncé car c'est un indice de taille pour la solution ...

ok pour une seconde fois!
on a montrer queg^n(x)=n(g(x)-x)+x
on suppose mnt l existance d un reel b tel que g(b) different de b
g^n(b)=n(g(b)-b)+b==> lim(g^n(b))=infini
or on a ; g^n(b)-g^n-1(b)=g^n-1(b)-b par passage a la limite on se trouve absurde d ou g(b)=b pour tt b
j espere que c claire mnt,le fait de considerer Un c juste pour ne pas ecrire a chaque fois g^n....

j ai pas vu ton message et ta raison il ya une faute qq part car la fonction x-->x+1 verifie la relation. mais ou est la faute :p c pas moi qui pourrai la trouver ! :p

maintenant, peut quelqu'un proposer un nouveau problème ?

y a pas encore de solution.

Othmaann a écrit:

Problème 3:
Trouver toutes les fonctions réelles et continues g vérifiant : g(g(x))=2g(x)-x

Solution du problème3:
on a (g(g(x))-g(x))/(g(x)-x)=1
Donc g est une fonction affine qui convient la condition de continuité de la fonction g sur R
Alors g s'écrit sous la forme de g(x)=x+b et g(g(x))=g(x)+b=x+2b=2(g(x))-x
Donc g(x)=x+b avec b appartenant a R.

Poste un problème je croix que c'est la bonne solution ...

Pour l'instant j'en ai aucun exercice intéressant vous pouvez poster.

Autre Solution du P3:

Il est trivial de remarquer que la fonction g(x)=x+n tel que n est un paramètre réel est une solution à cette équation reste à prouver qu'elle la seule

Par absurde supposons que g(x)=/x+n (=/ veut dire différent de)

On sait que si x<y alors g(g(x))<g(g(y))
donc selon la relation 2g(x)+y<2g(y)+x
alors on a 2g(x)+x<2g(x)+y<2g(y)+x donc g(x)<g(y)
alors g est strictement croissante d'où on déduit l'existence de la fonction g^(-1)(x) pour tous x de Dg

à l'aide de l'asseration P(g^(-1)(x)) on trouve que g(x)+g^(-1)(x)=2x pour tous x de Dg

pour tous x de Dg g(x)=/x+n équivaut g(x)=x+n+p tel que p est un réel non nul et non constant car s'il l'est on revient g(x)=x+m tel que m est un paramètre réel
alors g^(-1)(x)=/x-n-p donc g(x)+g^(-1)(x)=/2x ce qui se contredit avec le fait que g(x)+g^(-1)(x)=2x

CQFD (sauf erreur)

mr.mertasayeker a écrit:

Autre Solution du P3:

Il est trivial de remarquer que la fonction g(x)=x+n tel que n est un paramètre réel est une solution à cette équation reste à prouver qu'elle la seule

Par absurde supposons que g(x)=/x+n (=/ veut dire différent de)

On sait que si x<y alors g(g(x))<g(g(y))
donc selon la relation 2g(x)+y<2g(y)+x
alors on a 2g(x)+x<2g(x)+y<2g(y)+x donc g(x)<g(y)
alors g est strictement croissante d'où on déduit l'existence de la fonction g^(-1)(x) pour tous x de Dg

à l'aide de l'asseration P(g^(-1)(x)) on trouve que g(x)+g^(-1)(x)=2x pour tous x de Dg

pour tous x de Dg g(x)=/x+n équivaut g(x)=x+n+p tel que p est un réel non nul et non constant car s'il l'est on revient g(x)=x+m tel que m est un paramètre réel
alors g^(-1)(x)=/x-n-p donc g(x)+g^(-1)(x)=/2x ce qui se contredit avec le fait que g(x)+g^(-1)(x)=2x

CQFD (sauf erreur)

Comment t'a trouvé ce qui est en rouge.