| | Préparations aux olympiades de Terminale (2012) |  |
|
+23rimele judicecharatein mohamed diai yasserito tahasinbad the kiler darkpseudo Incompri M.Marjani boubou math samsoum05 kaj mima manazerty Misterayyoub nmo mr.mertasayeker az360 expert_run xyzakaria Othmaann ali-mes n.naoufal Mehdi.O 27 participants |
|
| Auteur | Message |
|---|
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Sam 10 Déc 2011, 15:15 Sam 10 Déc 2011, 15:15 | |
| L'exercice de rimele : - rimele a écrit:
- problème 45;
Soit P(x)=ax^3+bx ,on dit que le couple (a,b) est n-gentil si :
pour tout k et m de IN : n divise P(m)-p(k) ==> n divise m-k
on dit que le couple (a,b) est trés gentil si il est n-gentil pour une infinité de valeurs de n.
1) trouver un couple (a,b) qui est 51-gentil mais pas tres gentil!
2)prouver que tout les 2010-gentil sont trés gentil.. est enfin résolu ! En fait, il s'agit d'un IMO 2010 shortlist dont le corrigé est disponible ici. Si vous le voulez bien, voici le nouveau problème que je vous propose : Problème 47 :Trouver toutes les fonctions continues  telles que pour tous 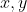 réels :  | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 | |
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 11 Déc 2011, 10:48 Dim 11 Déc 2011, 10:48 | |
| Ta solution me semble tout à fait correcte, az360. Si vous le voulez bien, je vous propose un nouveau problème. Soit x,y, et z des réels strictement positifs. Prouver que  Pour information, cette inégalité admet entre autres une preuve en une seule ligne.
Dernière édition par momo1729 le Dim 11 Déc 2011, 11:44, édité 1 fois | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 11 Déc 2011, 11:24 Dim 11 Déc 2011, 11:24 | |
| Edit : Pas problème momo 1729
Dernière édition par diablo902 le Dim 11 Déc 2011, 11:50, édité 2 fois | |
|
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 11 Déc 2011, 11:44 Dim 11 Déc 2011, 11:44 | |
| Excusez-moi, j'ai fait une erreur dans l'énoncé  . Il est à présent corrigé. Et désolé diablo902  Pour information, l'inégalité que j'avais proposé était venait de Iran TST 1996 et était loin d'être évidente  | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 11 Déc 2011, 12:44 Dim 11 Déc 2011, 12:44 | |
| Cette inégalité est un peu facile:- Spoiler:
Après caushy shwarz ^2}\geq&space;(\sum&space;\frac{a}{b+c})^2) on trouve l’inégalité de Nesbitt :  Ce qui est une application directe de C.S. 
| |
|
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 11 Déc 2011, 13:08 Dim 11 Déc 2011, 13:08 | |
| Ta solution est juste.
Je n'ai pas de problème à proposer pour le moment. | |
|
  | |
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 11 Déc 2011, 13:13 Dim 11 Déc 2011, 13:13 | |
| | |
|
  | |
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 11 Déc 2011, 13:29 Dim 11 Déc 2011, 13:29 | |
| Sinon je pense qu'il ya une petite généralisation de l'inégalité qu'a poster momo , ^n}+\frac{b^{n-1}}{(a+c)^n}+\frac{c^{n-1}}{(a+b)^n}\geq%20\frac{3^n}{2^n(a^{n-1}+b^{n-1}+c^{n-1})}) | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 11 Déc 2011, 13:47 Dim 11 Déc 2011, 13:47 | |
| Problème 49 :(Korea 1998) - Spoiler:
Soit I le centre du cercle inscrit du triangle ABC Prouvez Que : &space;\geq&space;AB^2&space;+&space;BC^2&space;+&space;CA^2)
Dernière édition par diablo902 le Ven 16 Déc 2011, 12:06, édité 1 fois | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 11 Déc 2011, 17:14 Dim 11 Déc 2011, 17:14 | |
| - Misterayyoub a écrit:
- momo1729 a écrit:
- Excusez-moi, j'ai fait une erreur dans l'énoncé
 . .
Il est à présent corrigé.
Et désolé diablo902 
Pour information, l'inégalité que j'avais proposé était venait de Iran TST 1996 et était loin d'être évidente  Est ce que tu es sur qu'il s'agit de iran tst 1996 
- Spoiler:
http://www.artofproblemsolving.com/Forum/viewtopic.php?f=51&t=378167&p=2089047&hilit=iran+tst+1996#p2089047
Il l'a proposé f lowl apres il edite leur poste . - Spoiler:
fhmtih ghalate
| |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 16 Déc 2011, 19:02 Ven 16 Déc 2011, 19:02 | |
| - diablo902 a écrit:
- Problème 49 :(Korea 1998)
Soit I le centre du cercle inscrit du triangle ABC
Prouvez Que : &space;\geq&space;AB^2&space;+&space;BC^2&space;+&space;CA^2) Je présente ma solution à cet exercice: *Je commence tout d'abord par la démonstrattion de quelques égalités qui vont m'aider pendant la démonstration: Soient X, Y et Z les projetés orthogonaux de I sur (AC), (CB) et (BA) respectivement. On pose ainsi: AX=x, CY=y et BZ=z. Selon Ravi, il est bien clair que AZ=x, CZ=y et BY=z. On a aussi AB=AZ+BZ=x+z, BC=BY+CY=z+y et CA=CX+AX=z+x. Soit r le rayon du cercle inscrit à ABC. -On est obligé maintenant à écrire r en fonction de x, y et z. On a (\frac{AB+BC+CA}{2}-AB)(\frac{AB+BC+CA}{2}-BC)(\frac{AB+BC+CA}{2}-CA)}) , selon la formule de héron. Et puisque: 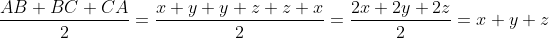 , la formule donnant la surface demeure: .(x+y+z-x-z)(x+y+z-y-z)(x+y+z-z-x)}) , ou encore: .x.y.z}) .==>(1) De plus, on sait que .r) .==>(2) De 1 et 2, il vient que .x.y.z}=(x+y+z).r) , donc 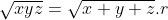 , soit en résumé 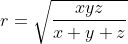 ou bien 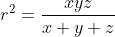 . -On a aussi selon le théorème de phytagore dans les triangles AIX, CIY et IBZ respectivement: 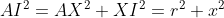 , 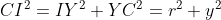 et 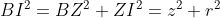 . *Maintenant, je reviens à l'inégalité proposée que je traite par équivalence successives: On a \ge AB^2+BC^2+CA^2) . Equivaut à \ge (x+y)^2+(y+z)^2+(z+x)^2) . Equivaut à \ge x^2+2xy+y^2+y^2+2yz+z^2+z^2+2zx+x^2) . Equivaut à 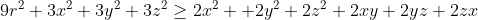 . Equivaut à ) . Afin de simplifier l'écriture, on pose encore x+y+z=p, xy+yz+zx=q et xyz=r. On a l'identité remarquable ^2=x^2+y^2+z^2+2(xy+yz+zx)) . Donc ^2-2(xy+yz+zx)=p^2-2q) . L'inégalité s'écrit donc 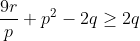 . Soit en multipliant par p: 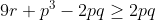 . Qui équivaut à 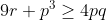 . Qui n'est autre que l'inégalité de shur. Ce qui veut bien dire que l'inégalité à démontré a été démontrée. L'égalité aura lieu si x=y=z, ainsi AB=BC=CA. C'est à dire lorsque ABC est un triangle équilatéral. CQFD. J'attends vos remarques et une confirmation. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 16 Déc 2011, 19:21 Ven 16 Déc 2011, 19:21 | |
| Je propose deux nouveaux exercices, pour relancer le jeu: Problème 50:Soient  ,  , 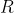 et  des polynômes vérifiant la relation: : P(x^5)+x.Q(x^5)+x^2.R(x^5)=(x^4+x^3+x^2+x+1).S(x)) . 1) Montrez que 1 est une racine du polynôme  . 2) 1 et-il une racine des polynômes  et 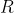 ? Problème 51:Déterminez le plus petit polynôme (qui a le plus petit degré) dont les coefficient sont des entiers relatifs, et dont le nombre complexe 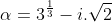 en est une racine. Bonne chance. | |
|
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 01 Jan 2012, 11:08 Dim 01 Jan 2012, 11:08 | |
| | |
|
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 01 Jan 2012, 18:39 Dim 01 Jan 2012, 18:39 | |
| Solution au problème 50 :Soit  . On a  . On a :  . Le déterminant du système formé par 3 équations quelconques des 4 ci-dessus est non-nul et il n'a donc qu'une solution :  | |
|
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 01 Jan 2012, 18:42 Dim 01 Jan 2012, 18:42 | |
| Problème 52:Soit  un polynôme à coefficients entiers et soit  des nombres premiers tels que  pour tout i entre 1 et n. Prouver qu'il existe un x tel que  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Jeu 12 Jan 2012, 15:28 Jeu 12 Jan 2012, 15:28 | |
| - momo1729 a écrit:
- Problème 52:
Soit  un polynôme à coefficients entiers et soit un polynôme à coefficients entiers et soit  des nombres premiers tels que des nombres premiers tels que  pour tout i entre 1 et n. pour tout i entre 1 et n.
Prouver qu'il existe un x tel que  Je présente ma solution: Je commence par considérer le système de congruences suivant: \\x\equiv x_2(q_2)\\\cdots\\x\equiv x_n(q_n)\end{cases}) . Ce système admet une solution d'après le théorème chinois. On remarque tout d'abord les lemmes suivants, dont la démonstration me semble triviale: Lemme 1: Soit q un nombrer premier et a un entier. Si ) , alors on a :q/P(a+n.q)) . Lemme 2: Soit p et q des nombres premiers et b un entier. Si ) et ) , alors ) . Soit M la solution du système de congruences. On a ) , donc on aura ) selon le lemme 1. On aura de même ) , ... et ) . Et vu que les entiers 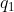 , 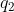 , ..., et 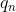 sont premiers, on aura forcément ) . Ce qui répond au problème. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 22 Jan 2012, 15:49 Dim 22 Jan 2012, 15:49 | |
| - Spoiler:
- nmo a écrit:
- Misterayyoub a écrit:
- Bon , je vous propose ce probleme pour refaire vivre ce topic ,
Probleme 44 :
Soit :
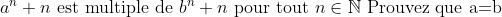
a et b appartiennent a IN Il y a quatre jours que j'ai la solution, mais je n'ai pas pu la rédiger ici.
Et enfin, la voici:
*Premièrement, on a le lemme suivant:
Soit p un entier.
Si p a autant de diviseurs que l'on veut, alors il est nul.
La démonstration découle immédiatement du fait que l'enseble des diviseurs d'un entier non nul est fini (C'est à dire que si p est non nul, alors il admet un nombre fini de diviseurs), et puis l'utilisation de l'implication contraposée.
*Deuxièmement, on a le deuxième lemme:
Soient p, x et m trois entiers.
Si 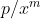 , alors , alors 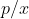 . .
Et pour ce qui est de la démonstration, on supose que 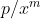 et on doit démontrer que et on doit démontrer que 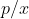 . .
Pour cela, on suppose par l'absurde que p ne divise pas x et soit 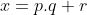 la division euclédienne de x par p (r est différent de 0). la division euclédienne de x par p (r est différent de 0).
On a ) , donc , donc ) . .
Et puisque r est différent de 0, il résulte que p ne divise pas 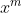 . .
Et cela constutue une contradiction avec 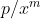 , donc ce qu'on a supposé est faux. , donc ce qu'on a supposé est faux.
Il résulte que 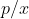 . .
*Maintenant, on revient à l'exercice:
On a selon l'énoncé: :b^n+n/a^n+n) . .
Je traite deux cas selon les valeurs de b:
-Cas premier: b=0.
On aura :0^n+n/a^n+n) , soit , soit :n/a^n+n) . .
Ou encore :n/a^n) , et ainsi , et ainsi :n/a) , selon le second lemme. , selon le second lemme.
Cela veut dire que a admet autant de diviseurs que l'on veut, donc a=0 selon le premier lemme.
On conclut que a=b=0, dans ce cas.
-Cas second: 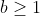 . .
On a: :b^n+n/a^n+n) . .
On prends n=b, on trouve que 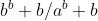 , soit , soit /a^b+b) . .
Ainsi :a^b+b=k.b(b^{b-1}+1)) . .
Donc :a^b=k.b(b^{b-1}+1)-b) , ou bien , ou bien :a^b=b\big(k.(b^{b-1}+1)-1\big)) . .
Il s'ensuit que 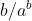 . .
Et donc 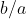 , selon le second lemme. , selon le second lemme.
D'où l'existence d'un entier t qui vérifie 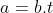 . .
La première relation de l'exercice s'écrit par conséquent: :b^n+n/(b.t)^n+n) . .
Ou encore :b^n+n/b^n.t^n+t^n.n-t^n.n+n=t^n(b^n+n)+n(1-t^n)) . .
Donc :b^n+n/n(1-t^n)) . .
Pour n=1, on aura :b+1/1-t) . .
Pour n=2, on aura :b^2+2/2(1-t^2)) . .
On itère la procédure autant de fois que l'on veut.
Or, on sait que :1-t/1-t^n) et que et que :1-t^n/n(1-t^n)) . .
Il en découle que, l'entier ) , lorsque n décrit l'ensemble des entiers naturels, a autant de diviseurs que l'on veut. , lorsque n décrit l'ensemble des entiers naturels, a autant de diviseurs que l'on veut.
C'est à dire que :n(1-t^n)=0) selon le premier lemme. selon le premier lemme.
Et puisque n est une variable, on aura forcément t=1.
Ainsi a=b, dans ce cas aussi.
-Conclusion:
Dans les deux cas, on a démontré que a=b.
CQFD.
Sauf erreur.
Svp je n'ai pas arrivé a comprendre le deuxieme lemme: si p/x^m on a p/x . Est que p est premier? si c'est le cas c'est juste sinon je ne pense pas que ce lemme est juste pour tout p de IN. Contre-exemple:9/3^2 mais 9 ne divise pas 3. Excusez la banalité de ma question mais je voudrais avoir une clarification sur la véracité de ce lemme. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 22 Jan 2012, 16:00 Dim 22 Jan 2012, 16:00 | |
| Je crois qu'on doit ajouter une condition: p doit être inférieure à x , condition qui n'est pas présente ni dans votre passage de b/a^b --à-- b/a car du faite que (b^n+n)/(a^n+n) on a b<a
ni dans votre passage de n/a^n a n/a car a ne peut pas etre postérieur à n quelque soit ce derniere dans IN....
J'attends vos remarques sur ce sujet svp !
| |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mar 24 Jan 2012, 14:47 Mar 24 Jan 2012, 14:47 | |
| - yasserito a écrit:
- Spoiler:
- nmo a écrit:
- Misterayyoub a écrit:
- Bon , je vous propose ce probleme pour refaire vivre ce topic ,
Probleme 44 :
Soit :
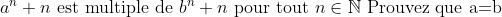
a et b appartiennent a IN Il y a quatre jours que j'ai la solution, mais je n'ai pas pu la rédiger ici.
Et enfin, la voici:
*Premièrement, on a le lemme suivant:
Soit p un entier.
Si p a autant de diviseurs que l'on veut, alors il est nul.
La démonstration découle immédiatement du fait que l'enseble des diviseurs d'un entier non nul est fini (C'est à dire que si p est non nul, alors il admet un nombre fini de diviseurs), et puis l'utilisation de l'implication contraposée.
*Deuxièmement, on a le deuxième lemme:
Soient p, x et m trois entiers.
Si 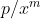 , alors , alors 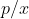 . .
Et pour ce qui est de la démonstration, on supose que 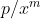 et on doit démontrer que et on doit démontrer que 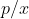 . .
Pour cela, on suppose par l'absurde que p ne divise pas x et soit 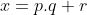 la division euclédienne de x par p (r est différent de 0). la division euclédienne de x par p (r est différent de 0).
On a ) , donc , donc ) . .
Et puisque r est différent de 0, il résulte que p ne divise pas 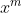 . .
Et cela constutue une contradiction avec 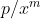 , donc ce qu'on a supposé est faux. , donc ce qu'on a supposé est faux.
Il résulte que 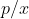 . .
*Maintenant, on revient à l'exercice:
On a selon l'énoncé: :b^n+n/a^n+n) . .
Je traite deux cas selon les valeurs de b:
-Cas premier: b=0.
On aura :0^n+n/a^n+n) , soit , soit :n/a^n+n) . .
Ou encore :n/a^n) , et ainsi , et ainsi :n/a) , selon le second lemme. , selon le second lemme.
Cela veut dire que a admet autant de diviseurs que l'on veut, donc a=0 selon le premier lemme.
On conclut que a=b=0, dans ce cas.
-Cas second: 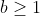 . .
On a: :b^n+n/a^n+n) . .
On prends n=b, on trouve que 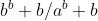 , soit , soit /a^b+b) . .
Ainsi :a^b+b=k.b(b^{b-1}+1)) . .
Donc :a^b=k.b(b^{b-1}+1)-b) , ou bien , ou bien :a^b=b\big(k.(b^{b-1}+1)-1\big)) . .
Il s'ensuit que 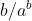 . .
Et donc 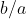 , selon le second lemme. , selon le second lemme.
D'où l'existence d'un entier t qui vérifie 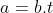 . .
La première relation de l'exercice s'écrit par conséquent: :b^n+n/(b.t)^n+n) . .
Ou encore :b^n+n/b^n.t^n+t^n.n-t^n.n+n=t^n(b^n+n)+n(1-t^n)) . .
Donc :b^n+n/n(1-t^n)) . .
Pour n=1, on aura :b+1/1-t) . .
Pour n=2, on aura :b^2+2/2(1-t^2)) . .
On itère la procédure autant de fois que l'on veut.
Or, on sait que :1-t/1-t^n) et que et que :1-t^n/n(1-t^n)) . .
Il en découle que, l'entier ) , lorsque n décrit l'ensemble des entiers naturels, a autant de diviseurs que l'on veut. , lorsque n décrit l'ensemble des entiers naturels, a autant de diviseurs que l'on veut.
C'est à dire que :n(1-t^n)=0) selon le premier lemme. selon le premier lemme.
Et puisque n est une variable, on aura forcément t=1.
Ainsi a=b, dans ce cas aussi.
-Conclusion:
Dans les deux cas, on a démontré que a=b.
CQFD.
Sauf erreur.
Svp je n'ai pas arrivé a comprendre le deuxieme lemme: si p/x^m on a p/x .
Est que p est premier? si c'est le cas c'est juste sinon je ne pense pas que ce lemme est juste pour tout p de IN.
Contre-exemple:9/3^2 mais 9 ne divise pas 3.
Excusez la banalité de ma question mais je voudrais avoir une clarification sur la véracité de ce lemme. Oui, tu as raison. P doit être un entier premier. - yasserito a écrit:
- Je crois qu'on doit ajouter une condition: p doit être inférieure à x , condition qui n'est pas présente ni dans votre passage de b/a^b --à-- b/a car du faite que (b^n+n)/(a^n+n) on a b<a
ni dans votre passage de n/a^n a n/a car a ne peut pas etre postérieur à n quelque soit ce derniere dans IN....
J'attends vos remarques sur ce sujet svp ! Oublie cette solution mon cher, je pense qu'on a eu une réponse parfaite pour ce problème autre que celle-là. Prière de chercher là-bas quelque part. Logiquement, on doit passer à un autre exercice. (Je prends l'initiative de chercher un) Je veux savoir si quelqu'un a eu la convocation à Rabat parce qu'il ne reste que peu de temps. Je me demande encore si quelqu'un sait les résultats de chaque région. Merci d'avance. | |
|
  | |
momo1729
Maître
 Nombre de messages : 82 Nombre de messages : 82
Age : 29
Date d'inscription : 28/09/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mar 24 Jan 2012, 15:57 Mar 24 Jan 2012, 15:57 | |
| Vous pouvez contacter Mr. Moussaoui (moussaoui359@gmail.com) pour des détails sur les noms des admis. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mar 24 Jan 2012, 20:42 Mar 24 Jan 2012, 20:42 | |
| Je propose ces deux exercices afin de se préparer pour les stages: Problème 53:N est un entier de 20 chiffres tel que 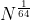 soit un entier. Quel est cet entier? Problème 54:Soient m et n deux entiers strictement positifs tel que 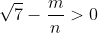 . Montrez que 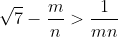 . Bonne chance. | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mar 24 Jan 2012, 21:14 Mar 24 Jan 2012, 21:14 | |
| Solution au problème 53:- Spoiler:
http://www.wolframalpha.com/input/?i=2^{64}
| |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mar 24 Jan 2012, 21:37 Mar 24 Jan 2012, 21:37 | |
| Solution au problème 53:- Spoiler:
On a 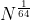 est un entier => il existe un k de IN tel que k^64=N. supposons que k>=3 alors k^3>=27>10 et ainsi k^60>10^20 et alors k^64>10^21 alors N>10^21 et ainsi N contient plus que 20 chiffres. Alors 0=<k=<2 et ainsi k=2 est la seule solution. Alors l'entier N qui a 20 chiffres tel que 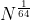 est un entier est 2^64. Sauf erreur.
| |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Jeu 02 Fév 2012, 12:14 Jeu 02 Fév 2012, 12:14 | |
| - nmo a écrit:
- Problème 54:
Soient m et n deux entiers strictement positifs tel que 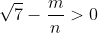 . .
Montrez que 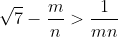 . . Voici ma solution: ---L'idée de la résolution repose sur le fait de remarquer que si un entier k vérifie 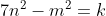 , alors on a forcémént: 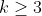 . *L'hypothèse de départ implique que: 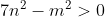 , et ainsi 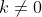 . *Supposons qu'on a l'égalité: 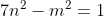 , et démontrons que cela mène vers une contradiction. On sait que quelquesoit l'entier p, on a ) ou ) . C'est à dire ) ou ) .==>(1) Et ) ou ) .==>(2) De (1) et (2), on trouve que ) ou ) ou ) . Tandis que ) . D'où l'impossibilité de cette égalité. *Supposons qu'on a l'égalité: 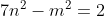 , et démontrons que cela mène vers une contradiction comme dans le cas dernier. On sait que quelquesoit l'entier p, on a ) ou ) ou ) C'est à dire ) ou ) ou ) .==>(3) Et ) ou ) ou ) .==>(4) De (3) et (4), on trouve que ) ou ) ou ) ou ) ou ) . Tandis que ) . D'où l'impossibilité de cette égalité. *Synthèse: On a démontré que 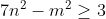 . ---On a 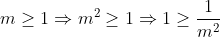 . Donc ^2) . Et par conséquent 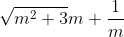 .==>(5) D'autre part, on a 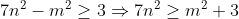 ou encore 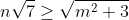 .==>(6) De (5) et (6), il vient 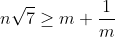 . Donc 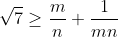 . Et finalement 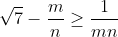 . ---CQFD. Sauf erreur. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  | |
| |
|
  | |
| | Préparations aux olympiades de Terminale (2012) |  |
|
