| | Préparations aux olympiades de Terminale (2012) |  |
|
+23rimele judicecharatein mohamed diai yasserito tahasinbad the kiler darkpseudo Incompri M.Marjani boubou math samsoum05 kaj mima manazerty Misterayyoub nmo mr.mertasayeker az360 expert_run xyzakaria Othmaann ali-mes n.naoufal Mehdi.O 27 participants |
|
| Auteur | Message |
|---|
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 29 Juil 2011, 00:33 Ven 29 Juil 2011, 00:33 | |
| Mehdi.O peut-on passer à un autre problème? | |
|
  | |
mr.mertasayeker
Féru
 Nombre de messages : 65 Nombre de messages : 65
Age : 29
Localisation : somewhere in morocco
Date d'inscription : 13/03/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 29 Juil 2011, 00:43 Ven 29 Juil 2011, 00:43 | |
| oui vous avais raison Mehdi.O mais il reste préférable d'aborder les problèmes qui nous seront bénéfiques pour ce moment non pas nous torturer avec des rudes épreuves qui ne seront d'aucune utilité durant cette période Peut-être faut penser à poster des exos sous forme d'application non connue de quelques théorèmes qui nous aideront pour améliorer le niveau des participants. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 29 Juil 2011, 00:51 Ven 29 Juil 2011, 00:51 | |
| Oui c'est ce que je voulais dire  . Alors si quelqu'un a un problème abordable qu'il le postes  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 29 Juil 2011, 12:11 Ven 29 Juil 2011, 12:11 | |
| - Othmaann a écrit:
- Problème 3:
Trouver toutes les fonctions réelles et continues g vérifiant : g(g(x))=2g(x)-x Je crois que le délai s'est largement écoulé. Merci de proposer une solution, si tu l'as. - Mehdi.O a écrit:
- Oui c'est ce que je voulais dire
 . .
Alors si quelqu'un a un problème abordable qu'il le postes  Je vous propose trois exercices, qui traitent de l'arithmétique, à la fois: Exercice 5:Soit a, b, c, d, e, et f six nombres entiers naturels différents deux à deux. On pose S=a+b+c+d+e+f, P=ab+bc+ca-de-ef-fd et R=abc+def. On suppose que S divise les deux nombres P et R. Démontrez que S ne peut pas être un nombre premier. Exercice 6:Démontrez qu'il existe une infinité de nombres entiers p qui satisfait les deux conditions: 1- p, p+6 et p+12 sont premiers. 2- p+1, p+2, p+3, p+4, p+5, p+7, p+8, p+9, p+10 et p+11 ne sont pas premiers. Exercice 7:Démontrez que: !\times (4n)!}{(m+n)!\times(2m)!\times(2n)!\times m!\times n!}) est un entiers quelque soient les deux entiers m et n. Bonne chance.
Dernière édition par nmo le Ven 29 Juil 2011, 14:24, édité 1 fois | |
|
  | |
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 29 Juil 2011, 13:53 Ven 29 Juil 2011, 13:53 | |
| - nmo a écrit:
- Othmaann a écrit:
- Problème 3:
Trouver toutes les fonctions réelles et continues g vérifiant : g(g(x))=2g(x)-x Je crois que le délai s'est largement écoulé.
Merci de proposer une solution, si tu l'as.
- Mehdi.O a écrit:
- Oui c'est ce que je voulais dire
 . .
Alors si quelqu'un a un problème abordable qu'il le postes  Je vous propose trois exercices, qui traitent de l'arithmétique, à la fois:
Exercice 5:
Soit a, b, c, d, e, et f six nombres entiers naturels différents deux à deux.
On pose S=a+b+c+d+e+f, P=ab+bc+ca-de-ef-fe et R=abc+def.
On suppose que S divise les deux nombres P et R.
Démontrez que S ne peut pas être un nombre premier.
Exercice 6:
Démontrez qu'il existe une infinité de nombres entiers p qui satisfait les deux conditions:
1- p, p+6 et p+12 sont premiers.
2- p+1, p+2, p+3, p+4, p+5, p+7, p+8, p+9, p+10 et p+11 ne sont pas premiers.
Exercice 7:
Démontrez que: !\times (4n)!}{(m+n)!\times(2m)!\times(2n)!\times m!\times n!}) est un entiers quelque soient les deux entiers m et n. est un entiers quelque soient les deux entiers m et n.
Bonne chance. tu veux dire -df non ? | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 29 Juil 2011, 14:23 Ven 29 Juil 2011, 14:23 | |
| - Misterayyoub a écrit:
- tu veux dire -df non ?
Effectivement. C'est édité. | |
|
  | |
manazerty
Maître
 Nombre de messages : 123 Nombre de messages : 123
Date d'inscription : 29/06/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Jeu 04 Aoû 2011, 01:45 Jeu 04 Aoû 2011, 01:45 | |
| - nmo a écrit:
- Othmaann a écrit:
- Problème 3:
Trouver toutes les fonctions réelles et continues g vérifiant : g(g(x))=2g(x)-x Je crois que le délai s'est largement écoulé.
Merci de proposer une solution, si tu l'as.
- Mehdi.O a écrit:
- Oui c'est ce que je voulais dire
 . .
Alors si quelqu'un a un problème abordable qu'il le postes  Je vous propose trois exercices, qui traitent de l'arithmétique, à la fois:
Exercice 5:
Soit a, b, c, d, e, et f six nombres entiers naturels différents deux à deux.
On pose S=a+b+c+d+e+f, P=ab+bc+ca-de-ef-fd et R=abc+def.
On suppose que S divise les deux nombres P et R.
Démontrez que S ne peut pas être un nombre premier.
Exercice 6:
Démontrez qu'il existe une infinité de nombres entiers p qui satisfait les deux conditions:
1- p, p+6 et p+12 sont premiers.
2- p+1, p+2, p+3, p+4, p+5, p+7, p+8, p+9, p+10 et p+11 ne sont pas premiers.
Exercice 7:
Démontrez que: !\times (4n)!}{(m+n)!\times(2m)!\times(2n)!\times m!\times n!}) est un entiers quelque soient les deux entiers m et n. est un entiers quelque soient les deux entiers m et n.
Bonne chance. .
Dernière édition par manazerty le Ven 05 Aoû 2011, 14:20, édité 1 fois | |
|
  | |
n.naoufal
Expert sup

 Nombre de messages : 595 Nombre de messages : 595
Age : 33
Localisation : France.
Date d'inscription : 05/11/2008
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Jeu 04 Aoû 2011, 23:04 Jeu 04 Aoû 2011, 23:04 | |
| L'exercice 6 est copié du livre de 6 ème année, celui qui le prouvera aura le droit à la médaille de FIELDS (Conjoncture des nombres premiers jumeaux) surtout pour la première condition.  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 05 Aoû 2011, 12:55 Ven 05 Aoû 2011, 12:55 | |
| - n.naoufal a écrit:
- L'exercice 6 est copié du livre de 6 ème année, celui qui le prouvera aura le droit à la médaille de FIELDS (Conjoncture des nombres premiers jumeaux) surtout pour la première condition.
 On peut s'aider du lien suivant: http://serge.mehl.free.fr/anx/nbprem_sexy.html. Dans notre cas, on cherche à prouver l'existance des suites de nombres premiers sexy d'ordre 3. Et pour aller plus loin: http://fr.wikipedia.org/wiki/Conjecture_de_De_Polignac. Ce résultat n'est pas encore.
Dernière édition par nmo le Ven 05 Aoû 2011, 13:14, édité 1 fois | |
|
  | |
manazerty
Maître
 Nombre de messages : 123 Nombre de messages : 123
Date d'inscription : 29/06/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 05 Aoû 2011, 13:02 Ven 05 Aoû 2011, 13:02 | |
| - n.naoufal a écrit:
- L'exercice 6 est copié du livre de 6 ème année, celui qui le prouvera aura le droit à la médaille de FIELDS (Conjoncture des nombres premiers jumeaux) surtout pour la première condition.
 .
Dernière édition par manazerty le Ven 05 Aoû 2011, 14:19, édité 1 fois | |
|
  | |
manazerty
Maître
 Nombre de messages : 123 Nombre de messages : 123
Date d'inscription : 29/06/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 05 Aoû 2011, 13:52 Ven 05 Aoû 2011, 13:52 | |
|
Dernière édition par manazerty le Ven 05 Aoû 2011, 14:18, édité 1 fois | |
|
  | |
manazerty
Maître
 Nombre de messages : 123 Nombre de messages : 123
Date d'inscription : 29/06/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 05 Aoû 2011, 13:58 Ven 05 Aoû 2011, 13:58 | |
|
Dernière édition par manazerty le Ven 05 Aoû 2011, 14:18, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 05 Aoû 2011, 14:08 Ven 05 Aoû 2011, 14:08 | |
| - Othmaann a écrit:
- Problème 3:
Trouver toutes les fonctions réelles et continues g vérifiant : g(g(x))=2g(x)-x Je vous propose de lire les solutions suivantes:  Après avoir démontré que f est une bijection sur  , il s'ensuit que f admet une bijection réciproque g.   Au plaisir. | |
|
  | |
mr.mertasayeker
Féru
 Nombre de messages : 65 Nombre de messages : 65
Age : 29
Localisation : somewhere in morocco
Date d'inscription : 13/03/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mer 10 Aoû 2011, 01:13 Mer 10 Aoû 2011, 01:13 | |
| hého avez vous oubliez ce sujet durant ramadan ou quoi  | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mer 10 Aoû 2011, 01:25 Mer 10 Aoû 2011, 01:25 | |
| quelqu'un poste un problème (difficulté moyenne hhhh) !!!  | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mer 10 Aoû 2011, 02:28 Mer 10 Aoû 2011, 02:28 | |
| Mais il y a encore de problèmes sans solutions! - nmo a écrit:
Je vous propose trois exercices, qui traitent de l'arithmétique, à la fois:
Exercice 5:
Soit a, b, c, d, e, et f six nombres entiers naturels différents deux à deux.
On pose S=a+b+c+d+e+f, P=ab+bc+ca-de-ef-fd et R=abc+def.
On suppose que S divise les deux nombres P et R.
Démontrez que S ne peut pas être un nombre premier.
Exercice 6:
Démontrez qu'il existe une infinité de nombres entiers p qui satisfait les deux conditions:
1- p, p+6 et p+12 sont premiers.
2- p+1, p+2, p+3, p+4, p+5, p+7, p+8, p+9, p+10 et p+11 ne sont pas premiers.
Exercice 7:
Démontrez que: !\times (4n)!}{(m+n)!\times(2m)!\times(2n)!\times m!\times n!}) est un entiers quelque soient les deux entiers m et n. est un entiers quelque soient les deux entiers m et n.
Bonne chance. | |
|
  | |
samsoum05
Débutant
 Nombre de messages : 7 Nombre de messages : 7
Age : 30
Date d'inscription : 04/03/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Jeu 11 Aoû 2011, 13:25 Jeu 11 Aoû 2011, 13:25 | |
| Bonsoir frères et soeurs , s'il vous plait j'ai besoin de votre aide pour accomplir ce devoir , surtout la 1ère question car je ne sais meme pas d'ou commencer , Voila l'epreuve Et Merci  | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Ven 12 Aoû 2011, 21:38 Ven 12 Aoû 2011, 21:38 | |
| Euuh, ce n'est pas l'endroit convenable pour déposer ton épreuve, ce sujet est conçu pour une préparation des olympiades de terminale, comme juste son titre l'indique. Tu pourrais créer un sujet à part. Amicalement  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Sam 13 Aoû 2011, 16:03 Sam 13 Aoû 2011, 16:03 | |
| - nmo a écrit:
- Exercice 7:
Démontrez que: !\times (4n)!}{(m+n)!\times(2m)!\times(2n)!\times m!\times n!}) est un entiers quelque soient les deux entiers m et n. est un entiers quelque soient les deux entiers m et n. Voici ma réponse: Soit p un nombre premier. Selon la formule de Legendre, on a: *l'exposant de p dans la décomposition de !) en facteurs premiers est ) . -l'exposant de p dans la décomposition de !) en facteurs premiers est ) . -l'exposant de p dans la décomposition de !) en facteurs premiers est ) . -l'exposant de p dans la décomposition de 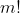 en facteurs premiers est ) . -l'exposant de p dans la décomposition de 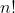 en facteurs premiers est ) . *l'exposant de p dans la décomposition de !) en facteurs premiers est ) . -l'exposant de p dans la décomposition de !) en facteurs premiers est ) . Ainsi, pour démontrez le résultat voulu on est amené à démontrer que +E\big(\frac{4n}{p^k}\big)\ge E\big(\frac{m+n}{p^k}\big)+E\big(\frac{2m}{p^k}\big)+E\big(\frac{2n}{p^k}\big)+E\big(\frac{m}{p^k})+E\big(\frac{n}{p^k}\big)) pour tout entier k. En guise de simplification, on pose: 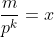 et 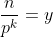 . L'inégalité est alors équivalente à +E(4y)\ge E(x)+E(y)+E(2x)+E(2y)+E(x+y)) pour tout rééls x et y. Ce qui est toujours vrai. Et cela achève la démonstration. Sauf erreur. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 14 Aoû 2011, 19:17 Dim 14 Aoû 2011, 19:17 | |
| Continuons avec ce problème. Problème 8:Trouver le nombre des entiers positifs x qui vérifient la condition suivante: 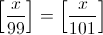 | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Dim 14 Aoû 2011, 23:51 Dim 14 Aoû 2011, 23:51 | |
|
Dernière édition par ali-mes le Lun 15 Aoû 2011, 00:22, édité 1 fois | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 15 Aoû 2011, 00:03 Lun 15 Aoû 2011, 00:03 | |
| C'est faux. Déjà le card(S)=50 dans ton cas mais c'est pas la bonne réponse car il y a d'autres choses que tu as négligé. | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 15 Aoû 2011, 01:29 Lun 15 Aoû 2011, 01:29 | |
| - expert_run a écrit:
- Continuons avec ce problème.
Problème 8:
Trouver le nombre des entiers positifs x qui vérifient la condition suivante:
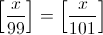 Solution au probleme : on a : E(x/99) = E(x/101) = d alors : 99d <= x < 99d+99 et 101d <= x < 101x + 101 alors Union de deux ensemble est : 101d <= x < 99d + 99 . donc pour d = 0 alors le nombre de sol est 99 . si : d = 1 ==> NBr_SOl = 97 ... si d = 49 alors Nbr_Sol = 1 . si d > 49 alors 101d > 99d+99 ce qui absurde . alors : NBR_ALL_SOl = 99 + 97 + ... + 1 = 50² . C.Q.F.E P.S : je n'ai pas de problemes a proposé ...  | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 | |
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 15 Aoû 2011, 02:02 Lun 15 Aoû 2011, 02:02 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  | |
| |
|
  | |
| | Préparations aux olympiades de Terminale (2012) |  |
|
