| | Préparations aux olympiades de Terminale (2012) |  |
|
+23rimele judicecharatein mohamed diai yasserito tahasinbad the kiler darkpseudo Incompri M.Marjani boubou math samsoum05 kaj mima manazerty Misterayyoub nmo mr.mertasayeker az360 expert_run xyzakaria Othmaann ali-mes n.naoufal Mehdi.O 27 participants |
|
| Auteur | Message |
|---|
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 15 Aoû 2011, 02:09 Lun 15 Aoû 2011, 02:09 | |
| - nmo a écrit:
Exercice 5:
Soit a, b, c, d, e, et f six nombres entiers naturels différents deux à deux.
On pose S=a+b+c+d+e+f, P=ab+bc+ca-de-ef-fd et R=abc+def.
On suppose que S divise les deux nombres P et R.
Démontrez que S ne peut pas être un nombre premier.
Bonne chance. Je pense que ce problème d'arithmétique est encore en jeu.  | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 15 Aoû 2011, 02:20 Lun 15 Aoû 2011, 02:20 | |
| Oui mais on doit continuer car ça fait longtemps qu'il était ici et personne n'a répondu .
Alors Kaj mima si t'a un problème adorable veuillez le partager avec nous . | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 15 Aoû 2011, 02:30 Lun 15 Aoû 2011, 02:30 | |
| - expert_run a écrit:
- Oui mais on doit continuer car ça fait longtemps qu'il était ici et personne n'a répondu .
Alors Kaj mima si t'a un problème adorable veuillez le partager avec nous . t'a raison  . | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 15 Aoû 2011, 02:44 Lun 15 Aoû 2011, 02:44 | |
| Voici un petit problème.
Problème 9:
Soient x et y des réels positifs tel que : (y^3)+y=<x-(x^3)
Prouver que:
y<x<1 et (x^2) + (y^2)<1
| |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 15 Aoû 2011, 03:03 Lun 15 Aoû 2011, 03:03 | |
| - expert_run a écrit:
- Voici un petit problème.
Problème 9:
Soient x et y des réels positifs tel que : (y^3)+y=<x-(x^3)
Prouver que:
y<x<1 et (x^2) + (y^2)<1
Solution :
on a : x >= x^3 => x < 1 . alors : y + y^3 < x parce que x - y - y^3 >= x^3 >= 0 donc : y < x car y^3 >= 0 . Donc : y < x < 1 alors : il nous reste la douxieme : on a : y(y² + 1) <= x(1-x^2) => (y² + 1)/(1-x^2) <= x / y et on d'apres (*) : x/y < 1/y alors : (y² + 1)/(1-x^2) <= 1 / y ==> y^3 + y + x^2 <= 1 et on a : y² <= y alors : y² + x² < y^3 + y + x^2 <= 1  . | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 15 Aoû 2011, 03:12 Lun 15 Aoû 2011, 03:12 | |
| Probleme 10 : ABCD est un carré . DFC est un triangle isocèle en F d’où CFD = 150 . Montrer que : AFB est un triangle équilatéral .  | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 15 Aoû 2011, 05:07 Lun 15 Aoû 2011, 05:07 | |
| J'ai cru qu'il s'agit des problèmes de niveau terminale, et non des exercices de troisième ou tronc commun ! En tous cas, voici ma réponse car je veux poster un autre exercice  : Ma réponse pour le problème 10:- Spoiler:
Posons d'abord AB=BC=CD=AD=a. Et on a:  . Le triangle  est isocèle en F, donc:  .  . Et on a:  . Dans le triangle FCD, on a d'après Al-Kashi: =CD^2) =a^2)  FD^2=a^2\Rightarrow&space;FD=\frac{a}{\sqrt{2+\sqrt{3}}}) . Dans le triangle AFD, on ad 'après Al-Kashi: )  ) Et d'après la calculette, le nombre entre parenthèses est égal à 1. Donc AF²=a² => AF=a=AB (1) Et on FC=FD donc F appartient à la médiatrice du segment [CD], et Puisque ABCD est un carré la médiatrice de [CD] coîncide avec la médiatrice du segment [AB], donc F appartient à la médiatrice du segment [AB] donc: FA=FB : (2) De (1) et (2), on conclut que: FA=FB=AB donc le triangle AFB est équilatéral.
Je vais vous proposer un exercice de géométrie que j'ai trouvé très amusant à résoudre. Problème 11: (*) Soit X un point de demi-cercle de diamètre [AB] et soit Y le milieu de l'arc AX. Soit Z la projection de Y sur (BX), et F la deuxième intersection de (AZ) avec le demi-cercle. Soit E le milieu du segment [YZ], montrer que E, F et B sont collinéaires. | |
|
  | |
manazerty
Maître
 Nombre de messages : 123 Nombre de messages : 123
Date d'inscription : 29/06/2011
 | |
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 15 Aoû 2011, 17:28 Lun 15 Aoû 2011, 17:28 | |
| - manazerty a écrit:
- az360 a écrit:
- expert_run a écrit:
- Continuons avec ce problème.
Problème 8:
Trouver le nombre des entiers positifs x qui vérifient la condition suivante:
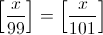 Solution au probleme :
on a : E(x/99) = E(x/101) = d alors : 99d <= x < 99d+99 et 101d <= x < 101x + 101 alors Union de deux ensemble est : 101d <= x < 99d + 99 . donc pour d = 0 alors le nombre de sol est 99 . si : d = 1 ==> NBr_SOl = 97 ... si d = 49 alors Nbr_Sol = 1 . si d > 49 alors 101d > 99d+99 ce qui absurde . alors :
NBR_ALL_SOl = 99 + 97 + ... + 1 = 50² . C.Q.F.E
P.S : je n'ai pas de problemes a proposé ... 
pourquoi? Parce Que : %20=%20(k+1)^2) c'est facile de la prouver par récurrence  . | |
|
  | |
manazerty
Maître
 Nombre de messages : 123 Nombre de messages : 123
Date d'inscription : 29/06/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 15 Aoû 2011, 17:39 Lun 15 Aoû 2011, 17:39 | |
| | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 15 Aoû 2011, 20:11 Lun 15 Aoû 2011, 20:11 | |
| Solution au problème 11:Soit C l'intersection de AY et BZ,H l'intersection de AX et BY, O le milieu de AB, et D l'intersection AX et BF. Il est bien clair que H est l'orthocentre du triangle ABC, et D l'orthocentre du triangle AZB. D'autre part, puisque Y est le milieu de l'arc AX, donc BY est bissectrice de l'angle {CBA}, ce qui implique que les deux triangles CYB et AYB sont isométriques ce qui implique que CB=BA, ensuite il est bien clair que les deux triangles CXY et ABC sont semblables alors on obtient directement YC=YX et ainsi Z est le milieu de CX, et puisque ZD || CH, alors D est le milieu de HX, mais puisque que les points B,X et Z sont collinéaires et les points B,H et Y sont collinéaires alors E_1 l'intersection de BF avec YZ est le milieu du segment YZ, ce qui coincide avec E et ainsi les points E,F et B sont collinéaires. 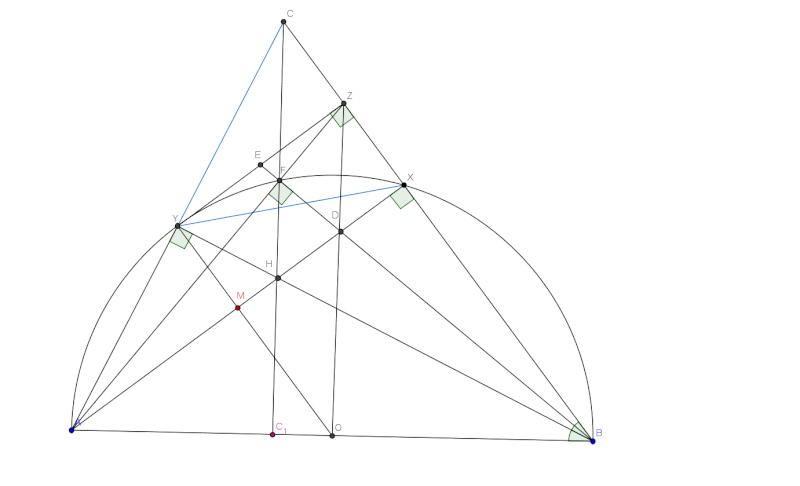 | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 15 Aoû 2011, 20:33 Lun 15 Aoû 2011, 20:33 | |
| - Mehdi.O a écrit:
- Solution au problème 11:
Soit C l'in............. Jolie Moi je n'arrive pas a resoudre  . alors propose un probleme ...  | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 15 Aoû 2011, 20:52 Lun 15 Aoû 2011, 20:52 | |
| Voici un joli problème d'arithmétique ( excusez-moi si c'est facile mais j'ai pas trouvé quelque chose de plus intéressant)
Problème 12:
Soit a,b,c trois entiers strictement positifs tel que a²/(a+b),b²/(b+c) et c²/(a+c) sont des nombres premiers.
Montrez que a=b=c. | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 15 Aoû 2011, 23:45 Lun 15 Aoû 2011, 23:45 | |
| Bravo mehdi.O, votre réponse est bonne. Voici ma réponse pour le problème 11: Soit O le milieu du segment [AB], donc O est le centreu du demi-cercle. On a Y est le milieu de l'arc AX, donc: YA=YX, donc: Y appartient à la médiatrice du segment [AX], et on a OA=OX, donc O appartient à la médiatrice du segment [AX]. On conclut que (OY) est la médiatrice du segment [AX], d'où: \perp%20(AX)) . Et on a: \perp%20(BX)\Rightarrow%20(AX)%20\perp%20(BZ)) . On conclut que: %20//%20(BZ)) , et ona Z la projection orthogonale de Y sur (BX), donc: \perp%20(BZ)\Rightarrow%20(OY)\perp%20(YZ)) . On conclut que la droite (YZ) est tangente au cercle de diamètre [AB] dans Y. :(1) On a:  . On considère le cercle (C') de diamètre [BZ], on a:  , donc: ) . On note T l'intersection de (BF) et (YZ). On a déjà montré que: \perp%20(BZ)\Rightarrow%20(TZ)\perp%20(BZ)) . Donc la droite (TZ) est tangente à (C') dans Z, donc d'après la théorème de la puissance d'un point par rapport à un cercle on a:  . De (1) on conclut que la droite (YE) est tangente au cercle de diamètre [AB] dans Y, donc d'après la théorème de la puissance d'un point par rapport à un cercle on a:  .  . Donc les points E, F et B sont collinéaires. CQFD.
Dernière édition par ali-mes le Lun 15 Aoû 2011, 23:55, édité 1 fois | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Lun 15 Aoû 2011, 23:54 Lun 15 Aoû 2011, 23:54 | |
| Solution de problème 12 Sois p un nombre premier. On a alors =bp\Rightarrow&space;\frac{a(a-p)}{p}\in&space;\mathbb{N}) et comme p est premier alors  on a ainsi  de la même façon on prouve que  , ainsi a=b=c CQFD | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mar 16 Aoû 2011, 00:18 Mar 16 Aoû 2011, 00:18 | |
| Problème 13 : Les diagonales d'un quadrilatère inscriptible ABCD se coupent en O .Prouver l'inégalité suivante:  | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mar 16 Aoû 2011, 02:05 Mar 16 Aoû 2011, 02:05 | |
| Je connais déjà cet exo car mon professeur de cette année me l'a proposé avant passer la dernière phase. Voici ma réponse, (car j'ai un bon exercice pour vous  ): Le quadrilatère est cyclique, donc: <BAC=<BDC <=> <BAO=<ODC. Et on a: <AOB=<DOC <=> les triangles OAB et OCD sont semblables. <=> OA/AB = OD/CD et OB/AB = OC/CD. <=> OA/OD = AB/CD et OB/OC = AB/CD. De même, <CAD=<DBC <=> <OAD=<OBC. Et on a: <AOB=<DOC <=> les triangles OAD et OBC sont semblables. <=> OA/AD = OB/BC et OD/AD = OC/BC. <=> OA/OB = AD/BC et OD/OC=AD/BC. D'après l'inégalité arithmétiquo-géométrique:  .  .  .  . La somme donne: \geq&space;2\left&space;(\frac{AB}{CD}+\frac{CD}{AB}+\frac{AD}{BC}+\frac{BC}{AD}&space;\right&space;)) . donc:  . D'où le résultat voulut. Veuillez m'informer si vous voyez une faute. Problème 14: (*) Soient a, b et c trois réels. Trouver toutes les valeurs de M tel que: (b-c)\;&space;\;&space;\;&space;(\forall&space;(a,b,c)\in&space;\mathbb{R}^3)) . EDIT: changement du problème. | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mar 16 Aoû 2011, 02:35 Mar 16 Aoû 2011, 02:35 | |
| Solution au probleme 14 :on pose : X = a-b et Y = b-c alors l'intégalité et equivalante a : x² + y² + xy >= Mxy alors : x² + y² >= (M-1)xy on sait que : x² + y² >= 2xy alors 2xy >= (M-1)xy (xy != 0) 2 >= M-1 => 3>=M .CQ.F.E  . | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mar 16 Aoû 2011, 02:48 Mar 16 Aoû 2011, 02:48 | |
| - az360 a écrit:
- Solution au probleme 14 :
on pose : X = a-b et Y = b-c alors l'intégalité et equivalante a :
x² + y² + xy >= Mxy
alors : x² + y² >= (M-1)xy
on sait que : x² + y² >= 2xy alors 2xy >= (M-1)xy (xy != 0)
2 >= M-1 => 3>=M .CQ.F.E  . . Il se peut que (M-1)xy >= 2xy, et x² + y² >= 2xy et x² + y² >= (M-1)xy les deux soient réalisés !! A toi de réctifier, par exemple: d'après:x² + y² >= (M-1)xy tu peux considérer un polynôme en x et étudier son signe. | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 | |
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mar 16 Aoû 2011, 03:08 Mar 16 Aoû 2011, 03:08 | |
| - az360 a écrit:
- ali-mes a écrit:
- az360 a écrit:
- Solution au probleme 14 :
on pose : X = a-b et Y = b-c alors l'intégalité et equivalante a :
x² + y² + xy >= Mxy
alors : x² + y² >= (M-1)xy
on sait que : x² + y² >= 2xy alors 2xy >= (M-1)xy (xy != 0)
2 >= M-1 => 3>=M .CQ.F.E  . .
Il se peut que (M-1)xy >= 2xy, et x² + y² >= 2xy et x² + y² >= (M-1)xy les deux soient réalisés !!
A toi de réctifier, par exemple: d'après:x² + y² >= (M-1)xy tu peux considérer un polynôme en x et étudier son signe. mais si on consédireons x = y != 0 alors on a : 2x² >= (M-1)x² <=> 2 >= M -1 !!!  M prendra ses valeurs quand x=y, et si par exemple x=2 et y=3, la condition x² + y² >= (M-1)xy doit être satisfaite pour tous les réels ! | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mar 16 Aoû 2011, 03:32 Mar 16 Aoû 2011, 03:32 | |
|
Dernière édition par az360 le Mar 16 Aoû 2011, 03:57, édité 1 fois | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mar 16 Aoû 2011, 03:40 Mar 16 Aoû 2011, 03:40 | |
| [quote="az360"] - az360 a écrit:
- Solution au probleme 14 :
on pose : X = a-b et Y = b-c alors l'intégalité et equivalante a :
x² + y² + xy >= Mxy
alors : x² + y² >= (M-1)xy
on sait que : x² + y² >= 2xy alors 2xy >= (M-1)xy (xy != 0)
-----------
nous avons la : 2xy >= (M-1)xy .
si xy > 0 alors : alors 2 >= M-1 => 3 >= M
si xy < 0 alors : 2 <= M-1 ==> 3 <= M
alors l'intersection de deux ensembles est : S = {3} .   C'est comme tu nous dis: on a 4>2 ( x² + y² >= (M-1)xy ) et on sait que : 4> 0 (x² + y² >= 2xy ) donc: 0>2 (2xy >= (M-1)xy ) ! C'est complètement illogique. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mar 16 Aoû 2011, 07:01 Mar 16 Aoû 2011, 07:01 | |
| - ali-mes a écrit:
Problème 14: (*)
Soient a, b et c trois réels. Trouver toutes les valeurs de M tel que:
(b-c)\;&space;\;&space;\;&space;(\forall&space;(a,b,c)\in&space;\mathbb{R}^3)) . .
EDIT: changement du problème. Solution du problème 14:On pose : X = a-b et Y = b-c Alors l'inégalité est équivalente à : x² + y² + xy >= Mxy alors : x² + y² >= (M-1)xy On pose t=M-1 Et p(x)=x² + y²-txy Donc pr tt x P(x)>=0 ==> Delta =<0 <=> |t|=<2 Alors M€[-1;3] CQFD
Problème 15:Trouver les triplets (a;b;c) des réels positifs ;solutions du système suivant  | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  Mar 16 Aoû 2011, 07:52 Mar 16 Aoû 2011, 07:52 | |
| - Spoiler:
Autre Solution pour 14 :x² + y² + xy >=Mxy donc : (x+y)² >= (m+1)xy et (x-y)² >= (M-3)xy alors : on pose y = -x dans 1 et y = x dans 2 . ce qui implique : m>=-1 et m<=3 C.G.F.D . 
| |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de Terminale (2012) Sujet: Re: Préparations aux olympiades de Terminale (2012)  | |
| |
|
  | |
| | Préparations aux olympiades de Terminale (2012) |  |
|
