Préparations aux olympiades de tronc commun (2011-2012 )

Comme j'ai fais le marathon d'exo mnt je crée une préparation considérée pour les tcéans du forum. Je commence par ces 3 exercices :
Exercice 1:
a,b 2 réels tel que :a^2+b^2=1 et a^3+b^3=-1
trouvez l'angle A qui permettent d'atteindre: cosA=a sinA=b
Exercice2:

Exercice3: un peu difficile
Résoudre dans R cette equation:


P.S. : les regles de cette préparation sont les mêmes du marathon

voici ma reponse pour le 3:
l'équation toukafi2ou : x^2+xvx - 2 =0 avec x>0 (racine)
donc x^2 - 1 + (vx)^3 -1 = 0
alors (x+1)(vx -1)(vx+1) + (vx-1)(x + vx+1)= 0
(Vx -1)(xVx +2x+2Vx+2)=0

D'ou Vx=1 ou xVx +2x +2Vx= -2

et puisque xVx+2x +2Vx >0 car x>0
donc on garde la première solution alors x=1

(l'exo d'avant n'est pas si difficile )

voici un exo: soit ABC un triangle rectangle en A tel que AB=8 AC=6 , calculez le rayon du cercle inscrit dans ce triangle

Ok je vais le résoudre
(merci rimetta)

de rien c'est ton tour

Réponse :2 Je vais ajouter 2 autre exo :
Exercice 5 :

Exercice 6 :

ex 5
on a puisque a b et c sont les cotés d'un triangle: a+b>=c , b+c>=a, a+c>=b
donc ac+bc >c^2 ab+ac>a^2 ab+bc> b^2
alors a^2+b^2+c^2 < 2ab +2ac +2bc
on rajoutant 2(ab+bc+ac) des deux cotés on constate le resultat

ex6
je l'ai resolu en N
on a x^2 +y^2 +z^2= 14 (x+y+z)^2 - 2(xy+yz+xz) = 14
alors 6^2 - 2(xy+yz+xz) = 14 xy+yz+xz= 11
on a d'apres la 2e equation (xy+yz+xz)/xyz = 11/6
donc xyz=6
on constate alors que (3,2,1) est la solution

Pour 5 Bravo 6 oué c juste pour N j'att tes exercice ( rimetta raki mjahda bezzaf tbarklah 3lik)

quelqu un pourait m'espliquer l'exo 5 et 6 SVPP !

Et pour l'exo de rimetta :
on doit d'abbord calculer BC en utlisant pythagore !
AB²+AC²=BC²
64+36=BC²
BC=10 .
On a r=(AB*AC) / AB + AC + CB
r= 48/8+6+10
r=48/24
r= 2

Et en fait l'exo 5 je pense que c'est faux sinon c'est mal copié !
(a+b+c)² N'égale pas a²+b²+c² Remitta !

Non c'est juste;
on rajoutant 2(ab+bc+ac) des deux cotés on constate le resultat

Comment ?
2(a²+b²+c²)>2(2ab +2bc+2ac)
DONC C'EST PAS JUSTE !
Sinn tu peux me le démontrer s'il te plait !
j'ai vraiment envie de comprendre ! STP DIABLO !

C'est simple:
a²+b²+c²=<2ab +2bc+2ac
a²+b²+c²+2ab +2bc+2ac=<4(ab+bc+ac)
(a+b+c)²=<4(ab+bc+ac) (puisque: (a+b+c)²=a²+b²+c²+2ab +2bc+2ac)

Kaj mima a démontré correctement. IL faut juste observer bien
(a+b+c)²=a²+b²+c²+2ab +2bc+2ac)

J'ajoute 2 autres Exos :
Exercice 7:

Spoiler:

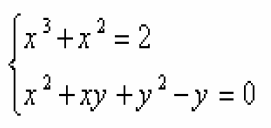
Exercice 8 :

Spoiler:

P,S,: Postez des exos;C n'est pas normal que je poste tout seul et vous les résolvez.

pour le premier
x^3+x²=2
x^3-1+x²-1=0
(x-1)(x²+x+1)+(x-1)(x+1)=0
(x-1)(x²+2x+2)=0
x=1 ou (x+1)²+1=0
x=1ou(x+1)²=-1c faux
donc x=1 on remplace dans la deuxiéme equation
1²+1*y+y²-y=0
1+y+y²-y=0
y²+1=0
y²=-1 c faux
alors le systeme n'a aucune solution dans R²

Solution de l'exercice 8

On a x <z +y

Donc x+1<z+y+1 d'ou x+1<y+z+1+yz

Donc x+1<(y+1)(z+1)

Donc

D'ou

Donc



Ainsi

Et puis

On conclut que

ET enfin

Amicalement

Solution de upsilon est juste
exo 8 est un exercice de 1 bac
J'attends vos exercices

Voici un autre exercice:

Exercice 9 :

Spoiler:

upsilon a écrit:

Voici un autre exercice:

Exercice 9 :

Spoiler:

upsilon tu rigoles ou quoi ;C'est un exo de 3 année de collège a+b>=2Vab (Ne poste pas ces faciles exos)

voici ma réponse pour l'exo 2:

posons : µ=x/a=y/b=z/c=(x+y+z)/(a+b+c)

V(ax)+V(by)+V(cz)=V((a^2)µ)+V((b^2)µ)+V((c^2)µ)

=V(µ) *(a+b+c)

=V(x+y+z)/(a+b+c) *V(a+b+c)^2

=V(x+y+z)(a+b+c)

pour l'exo 8,on peut utiliser la methode classique:

y/(y+1) + z/(z+1) - x/(x+1)

Ca nous donne : (y+2xy+z+xyz-x)/(x+1)(y+1)(z+1)

on [(x+1)(y+1)(z+1)] positif

et (y+2xy+z-x) positif

Donc y/(y+1) +z/(z+1) supérieur ou égale à x/(x+1)


MAIS la methode de Upsilon est la plus facile

Voici L'exo n° 9:


a et b deux reels positifs non nuls:

M.Q: 4V(ab) * (a+b) inférieur strictement à (Va+Vb)^4

Facile:
Solution d'exo 9 :

Spoiler: