| | Préparations aux olympiades de tronc commun (2011-2012 ) |  |
|
+16hind nassri Didou-Touzani Ahmed Taha (bis) Norax konica ali-mes Mehdi.O Nayssi oiga aminox upsilon salimreda kaj mima Soukaina Amaadour rimetta diablo902 20 participants |
|
| Auteur | Message |
|---|
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 15:21 Ven 11 Nov 2011, 15:21 | |
| rimetta J'att ta démo.
Et J'attends vos exos ou plutôt série (c'est mieux) | |
|
  | |
rimetta
Féru

 Nombre de messages : 57 Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 15:29 Ven 11 Nov 2011, 15:29 | |
| ma solution
on a xy+x+y=2
donc x²y²+ x²y +xy² = 2xy
et puisque x²y +xy² = - 8
donc en remplacant : x²y² - 8= 2xy
( xy+2)(xy - 4) = 0
alors xy = -2 ou xy= 4
on a xy(x+y) = -8 donc x+y= 4 ou x+y =- 2
donc (x+y)² = x²+y² + 2xy = 16 ou x² +y² + 2xy = 4
x²+y² = 20 ou x²+y² = -4 ( impossible)
on a alors x²+y² = 20
donc x²+y² - 2xy = 20 + 4 = 24
alors (x-y)² = 24 donc x-y =2V6 OU x-y= -2V6
alors x+y= 4 et x- y = 2V6 ou x+y=4 et x-y= -2V6
DONC LES SOLUTIONS : (2+V6 ,2-V6) et (2-V6 , 2+V6) | |
|
  | |
aminox
Maître
 Nombre de messages : 93 Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 15:39 Ven 11 Nov 2011, 15:39 | |
| Je l'ai résolue avec Delta et c'est plus facile
Dernière édition par aminox le Ven 11 Nov 2011, 16:06, édité 1 fois | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 15:52 Ven 11 Nov 2011, 15:52 | |
| Pour le 3eme Je pense : f(x)=x² | |
|
  | |
aminox
Maître
 Nombre de messages : 93 Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 16:58 Ven 11 Nov 2011, 16:58 | |
| - diablo902 a écrit:
- Pour le 3eme Je pense : f(x)=x²
effectivement : on trouve facilement : f(f(0))=f(0) f(0)=f(x²+f(x))-4f(x)² d' ou f(0)=0 puis f(f(x)+x²)=4x²f(x) d'ou f(x)=x² reciproque vraie ! | |
|
  | |
rimetta
Féru

 Nombre de messages : 57 Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 17:02 Ven 11 Nov 2011, 17:02 | |
| voila 3 autres mais un peu plus facils
trouvez n tel que V(17n+625) appartient a N et n est un nombre premier > 17
trouvez p tel que (p+47)/(p+22) appartent à N
quel est le plus petit nombre naturel que si on le divise par 24 , 18, 15 et 8 les restes sont respectivement 23 , 17 , 14,et 7 | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 17:15 Ven 11 Nov 2011, 17:15 | |
| Exo??
V(17n+625) appartient à IN <=> 17n+625=m² avec m de IN
<=> 17n=(m-25)(m+25)
Comme n premier > 17
n=m+25 et 17=m-25 <=> n=m+25 et m=42 <=> n=67 qui est bien premier
Exo??
(p+47)/(p+22) appartient a IN <=> 25/(p+22) appartient a IN
<=> 25=k(p+22) avec k de IN
25=5*5=(-5)*(-5)=25*1=(-25)*(-1)
...
Finalement on trouve {-17;-27;3;-23;-47;-21}
Exo??
Je ne donne pas la méthode car elle est évidente :
n=359
Dernière édition par Nayssi le Ven 11 Nov 2011, 17:21, édité 1 fois | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 17:19 Ven 11 Nov 2011, 17:19 | |
| Le 3eme est un exo de 3 année de collège  Nayssi bon retour allez postez qlq exos plus difficiles  | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 17:22 Ven 11 Nov 2011, 17:22 | |
| - aminox a écrit:
- diablo902 a écrit:
- Pour le 3eme Je pense : f(x)=x²
effectivement :
on trouve facilement :
f(f(0))=f(0)
f(0)=f(x²+f(x))-4f(x)² d' ou f(0)=0
puis f(f(x)+x²)=4x²f(x)
d'ou f(x)=x²
reciproque vraie ! Pourquoi? Merci Diablo902! Il faudra numéroter les exos parce que sinon on s'y perd! Exo?? On considère K et L deux points d’un cercle C de centre O. Soit A un point de la droite (KL) en dehors du cercle. On note P et Q les points de contact des tangentes à C issues de A. Soit M le milieu de [P Q]. Montrer que les angles <MKO et <MLO sont égaux Exo?? Soit f : IR -> IR et f(x)+f(x-1)=x² On suppose que f(19)=99 Calculer : f(94)
Dernière édition par Nayssi le Ven 11 Nov 2011, 17:57, édité 3 fois | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 17:28 Ven 11 Nov 2011, 17:28 | |
| - Nayssi a écrit:
- aminox a écrit:
- diablo902 a écrit:
- Pour le 3eme Je pense : f(x)=x²
effectivement :
on trouve facilement :
f(f(0))=f(0)
f(0)=f(x²+f(x))-4f(x)² d' ou f(0)=0
puis f(f(x)+x²)=4x²f(x)
d'ou f(x)=x²
reciproque vraie ! Pourquoi?
Merci Diablo902!
Il faudra numéroter les exos parce que sinon on s'y perd!
Exo??
On considère K et L deux points d’un cercle C de centre O. Soit A un point de la droite (KL)
en dehors du cercle. On note P et Q les points de contact des tangentes à C issues de A. Soit
M le milieu de [P Q]. Montrer que les angles <MKO et <MLO sont égaux Alors une petite recherche te donne le numéros | |
|
  | |
rimetta
Féru

 Nombre de messages : 57 Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 17:59 Ven 11 Nov 2011, 17:59 | |
| diablo902 je n vais pas inventer des exos difficils pour que tu sois à l'aise dailleurs j'ai mentionné qu'ils etaient facils donc c'est pas la peine que tu le redises
Dernière édition par rimetta le Ven 11 Nov 2011, 18:03, édité 1 fois | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 18:01 Ven 11 Nov 2011, 18:01 | |
| Un autre de Géométrie:Svp ne fait pas copier coller du solution dans les sites internet a,b et c les cotés d'un triangle et p son demi périmetre et S sa surface Prouver que: 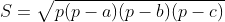 | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 18:08 Ven 11 Nov 2011, 18:08 | |
| - rimetta a écrit:
- diablo902 je n vais pas inventer des exos difficils pour que tu sois à l'aise dailleurs j'ai mentionné qu'ils etaient facils donc c'est pas la peine que tu le redises
rimetta ! ! ! tous les participants à cette préparation ont un sacré niveau au maths ;donc ne rigole pas en postant ces exos de 3 année ou du la 1er phase d'olympiade SVP; Postez les exos difficiles afin D'avoir un parfait niveau au math | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 | |
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 | |
  | |
aminox
Maître
 Nombre de messages : 93 Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 20:32 Ven 11 Nov 2011, 20:32 | |
| L'exo de diablo de géométrie f lktab dial had l3am "fi rihab riadiat"
| |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 21:06 Ven 11 Nov 2011, 21:06 | |
| - aminox a écrit:
- L'exo de diablo de géométrie f lktab dial had l3am "fi rihab riadiat"
Je savais pas ; Car c'est l'exo de oiga ;Je l'ai trouvé aussi dans un jeu d'été  | |
|
  | |
aminox
Maître
 Nombre de messages : 93 Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 21:15 Ven 11 Nov 2011, 21:15 | |
| mais c bien de le poster car f lmou9rar yalah khassk tbynha f "motlat 9aim zawiya moutassawi ssa9ayn" | |
|
  | |
aminox
Maître
 Nombre de messages : 93 Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 23:04 Ven 11 Nov 2011, 23:04 | |
| exo 14:
x>2
M.Q: x^3-3x-2>0 | |
|
  | |
aminox
Maître
 Nombre de messages : 93 Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 23:51 Ven 11 Nov 2011, 23:51 | |
| - diablo902 a écrit:
- Nayssi a écrit:
Exo??
Soit f : IR -> IR
et f(x)+f(x-1)=x²
On suppose que f(19)=99
Calculer : f(94) Réponse:
 Jai pas bien compris | |
|
  | |
oiga
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 28
Date d'inscription : 09/11/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Sam 12 Nov 2011, 00:55 Sam 12 Nov 2011, 00:55 | |
| - diablo902 a écrit:
- Nayssi a écrit:
Exo??
Soit f : IR -> IR
et f(x)+f(x-1)=x²
On suppose que f(19)=99
Calculer : f(94) Réponse:
 Diablo, vérifie tes calculs en suivant ta méthode j'ai trouvé autre chose (f(94)+f(93))-(f(93)+f(92))+......+(f(20) + f(19))=94² - 93² +92² -91² +93²-........+20² alors 94²-93² c'est x²-(x-1)²=(x-x+1)(x+x-1)=2x-1 alors 94²-93²=2*94-1 la même chose pour les autres paires successives alors (f(94)+f(93))-(f(93)+f(92))+......+(f(20) + f(19))=94² - 93² +92² -91² +93²-........+20² =2*94-1+2*92-1+2*90-1........2*20-1 on va calculez les moins uns -((94-20)/2 +1)= -36 alors notre équation = 2*94 +2*92 +2*90+......+2*20 -36 =2(94+92+...+20)-36 et pour calculez 2+4+6+....+n (n est pair) 2+4+6+....+n= n(n+2)/4 Pour la démontrer c'est la même méthode de 1+2+...+n=n(n+1)/2 alors =2(94(94+2)/4 - 18(18+2)/4) -36 =(94*96-18*20)/2 -36 =4296 Toi tu as trouvé 4655 Comment tu as fait ça??! Pourtant, bravo j'ai aimé ta méthode | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Sam 12 Nov 2011, 10:21 Sam 12 Nov 2011, 10:21 | |
| - Spoiler:
- oiga a écrit:
- diablo902 a écrit:
- Nayssi a écrit:
Exo??
Soit f : IR -> IR
et f(x)+f(x-1)=x²
On suppose que f(19)=99
Calculer : f(94) Réponse:

Diablo, vérifie tes calculs
en suivant ta méthode j'ai trouvé autre chose
(f(94)+f(93))-(f(93)+f(92))+......+(f(20) + f(19))=94² - 93² +92² -91² +93²-........+20²
alors 94²-93² c'est x²-(x-1)²=(x-x+1)(x+x-1)=2x-1
alors 94²-93²=2*94-1 la même chose pour les autres paires successives
alors
(f(94)+f(93))-(f(93)+f(92))+......+(f(20) + f(19))=94² - 93² +92² -91² +93²-........+20²
=2*94-1+2*92-1+2*90-1........2*20-1
on va calculez les moins uns
-((94-20)/2 +1)= -36
alors notre équation
= 2*94 +2*92 +2*90+......+2*20 -36
=2(94+92+...+20)-36
et pour calculez 2+4+6+....+n (n est pair)
2+4+6+....+n= n(n+2)/4
Pour la démontrer c'est la même méthode de 1+2+...+n=n(n+1)/2
alors
=2(94(94+2)/4 - 18(18+2)/4) -36
=(94*96-18*20)/2 -36
=4296
Toi tu as trouvé 4655
Comment tu as fait ça??!
Pourtant, bravo j'ai aimé ta méthode
oiga ; regarde bien : 94²-93²=(94-93)(94+93)= 94+93et il reste +20² sans -19² Ta méthode est la mienne mais tu n'as pas regardé qu'il n'y a pas -19² et tu as oublié f(19) Pour calculer il faut utiliser sigma dans calculatrice scientifique 
Dernière édition par diablo902 le Sam 12 Nov 2011, 11:15, édité 2 fois | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Sam 12 Nov 2011, 10:46 Sam 12 Nov 2011, 10:46 | |
| Réponse D'exo 14 :- Spoiler:
x²>4 --> x²-x>2 --> x²-x-2>0
Donc :(x+1)(x²-x-2)>0
Enfin : x^3-3x-2>0
C.Q.F.D. | |
|
  | |
rimetta
Féru

 Nombre de messages : 57 Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Sam 12 Nov 2011, 11:45 Sam 12 Nov 2011, 11:45 | |
| pour le 14 on peut juste factoriser ca donne (x+1)²(x-2) qui est > 0 puisque x>0
la demonstration de l'exo de geometrie est un peu longue mais il suffit de démontrer que OMLK roba3i dairi en remarquant les égalités entre les différents angles de la figure.
pour l'autre exo de géométrie je pense qu'il faut supposer que le triangle est isocèle puis rectangle | |
|
  | |
aminox
Maître
 Nombre de messages : 93 Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Sam 12 Nov 2011, 12:21 Sam 12 Nov 2011, 12:21 | |
| - rimetta a écrit:
- pour le 14 on peut juste factoriser ca donne (x+1)²(x-2) qui est > 0 puisque x>0
la demonstration de l'exo de geometrie est un peu longue mais il suffit de démontrer que OMLK roba3i dairi en remarquant les égalités entre les différents angles de la figure.
pour l'autre exo de géométrie je pense qu'il faut supposer que le triangle est isocèle puis rectangle Ouais ,c'est ce que j'ai dit mais f lmou9rar rah 3i bach ysshlou amma f bssh rah faut prendre un triangle w safi | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2011-2012 ) |  |
|
