| | Préparations aux olympiades de tronc commun (2011-2012 ) |  |
|
+16hind nassri Didou-Touzani Ahmed Taha (bis) Norax konica ali-mes Mehdi.O Nayssi oiga aminox upsilon salimreda kaj mima Soukaina Amaadour rimetta diablo902 20 participants |
|
| Auteur | Message |
|---|
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 | |
  | |
hind nassri
Maître

 Nombre de messages : 143 Nombre de messages : 143
Age : 29
Date d'inscription : 25/01/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Dim 01 Jan 2012, 21:30 Dim 01 Jan 2012, 21:30 | |
| c pa seul moi aussi jé po fé attention que p est un nombre premier | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Dim 01 Jan 2012, 21:31 Dim 01 Jan 2012, 21:31 | |
| - hind nassri a écrit:
- voici un vrai exercice l'autre exercice est deja resolu
trouvez (x;z;t;y)€ N
4/x =1/t+1/y +1/z
bon courage et bonne chance pour ton exo hind nassri j'ai trouvé que x=2 je l'ai trouvé b les inégalités | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Dim 01 Jan 2012, 21:34 Dim 01 Jan 2012, 21:34 | |
| - abdelkrim-amine a écrit:
- Didou-Touzani a écrit:
- abdelkrim je viens de voir ton equation je vais essayer de la résoudre d'une autre façon

(si'il y 'en a xD)
hind j'aimerais bien voir ton exo
boof voila un autre:
Déterminer tous les nombres n, carrés parfaits, tels que n=7p+4 où p est un nombre premier.
Allez bonne chance ! je pense que les seuls réponses c'est p=2 => n=16 ou p=3 => n=25 Solution : On pose n=m² de IN 7p+4=m² soit 7p=(m-2)(m+2) Ainsi : m-2=7 et m+2=p OU m-2=p et m+2=7 Soit : m=9 et p=11 OU m=5 et p=3 Donc n=81 (Dans ce cas p=11) ou n=25 (p=3) Finalement : S={25;81} | |
|
  | |
hind nassri
Maître

 Nombre de messages : 143 Nombre de messages : 143
Age : 29
Date d'inscription : 25/01/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Dim 01 Jan 2012, 21:42 Dim 01 Jan 2012, 21:42 | |
| - Didou-Touzani a écrit:
- selon des calculs un peu longs j'ai trouvé :
x=1 t=1/2 y=1 z=1
je vais posté ma demonstration par la suite  voici une solution t=y=z=3 et x=4 | |
|
  | |
Didou-Touzani
Habitué
 Nombre de messages : 20 Nombre de messages : 20
Age : 29
Localisation : Casablanca
Date d'inscription : 31/12/2011
 | |
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Dim 01 Jan 2012, 22:35 Dim 01 Jan 2012, 22:35 | |
| voici un autre exercice \left&space;(&space;3a-2b&space;\right&space;)=2ab&space;\\\\&space;calculer&space;\&space;\frac{a+b}{a-b}\\\\Bonne\&space;chance) | |
|
  | |
hind nassri
Maître

 Nombre de messages : 143 Nombre de messages : 143
Age : 29
Date d'inscription : 25/01/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Dim 01 Jan 2012, 22:48 Dim 01 Jan 2012, 22:48 | |
| | |
|
  | |
hind nassri
Maître

 Nombre de messages : 143 Nombre de messages : 143
Age : 29
Date d'inscription : 25/01/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Dim 01 Jan 2012, 22:52 Dim 01 Jan 2012, 22:52 | |
| apres developement on aura 3a²-7ab+2b²=0
=>(a-2b)(3a-2b)=0
=>a=2b ou 3a=2b
a+b)/(a-b)=3 ou (a+b)/(a-b)=-2 | |
|
  | |
hind nassri
Maître

 Nombre de messages : 143 Nombre de messages : 143
Age : 29
Date d'inscription : 25/01/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Dim 01 Jan 2012, 22:57 Dim 01 Jan 2012, 22:57 | |
| augmentez un peu le defi les matheux
nous voulons des exercices de casse-tête | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Dim 01 Jan 2012, 23:02 Dim 01 Jan 2012, 23:02 | |
| - hind nassri a écrit:
- apres developement on aura 3a²-7ab+2b²=0
=>(a-2b)(3a-2b)=0
=>a=2b ou 3a=2b
a+b)/(a-b)=3 ou (a+b)/(a-b)=-2 génial  je l'ai fait mais avec une grande méthode voila  | |
|
  | |
hind nassri
Maître

 Nombre de messages : 143 Nombre de messages : 143
Age : 29
Date d'inscription : 25/01/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Dim 01 Jan 2012, 23:12 Dim 01 Jan 2012, 23:12 | |
| ma methode est plus courte j'adore les courtes methodes  je vé poster mon exercice dm1 inchaalah | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Dim 01 Jan 2012, 23:14 Dim 01 Jan 2012, 23:14 | |
| - hind nassri a écrit:
- ma methode est plus courte
j'adore les courtes methodes 
je vé poster mon exercice dm1 inchaalah oui votre methode est plus courte OK | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Dim 01 Jan 2012, 23:18 Dim 01 Jan 2012, 23:18 | |
| Exercice ??:
Trouvez tous les entiers x,y>0 tels que : x!+3=y² | |
|
  | |
hind nassri
Maître

 Nombre de messages : 143 Nombre de messages : 143
Age : 29
Date d'inscription : 25/01/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Dim 01 Jan 2012, 23:20 Dim 01 Jan 2012, 23:20 | |
| - abdelkrim-amine a écrit:
- hind nassri a écrit:
- ma methode est plus courte
j'adore les courtes methodes 
je vé poster mon exercice dm1 inchaalah
oui votre methode est plus courte
OK vous savez abdelkrim la solution de mon exo (de x;t;y;z)ou pas encore ?? | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Dim 01 Jan 2012, 23:29 Dim 01 Jan 2012, 23:29 | |
| - hind nassri a écrit:
- abdelkrim-amine a écrit:
- hind nassri a écrit:
- ma methode est plus courte
j'adore les courtes methodes 
je vé poster mon exercice dm1 inchaalah
oui votre methode est plus courte
OK
vous savez abdelkrim la solution de mon exo (de x;t;y;z)ou pas encore ?? pas encore il y a bcp de solutions | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Lun 02 Jan 2012, 00:29 Lun 02 Jan 2012, 00:29 | |
| Exercice ?? :Démontrer que : 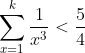 | |
|
  | |
hind nassri
Maître

 Nombre de messages : 143 Nombre de messages : 143
Age : 29
Date d'inscription : 25/01/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Lun 02 Jan 2012, 18:03 Lun 02 Jan 2012, 18:03 | |
| SLT TT le monde VOICI mon exercice : CALCULER : 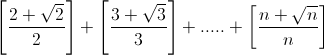 n€N bonne chance | |
|
  | |
Didou-Touzani
Habitué
 Nombre de messages : 20 Nombre de messages : 20
Age : 29
Localisation : Casablanca
Date d'inscription : 31/12/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Lun 02 Jan 2012, 18:08 Lun 02 Jan 2012, 18:08 | |
| - hind nassri a écrit:
- apres developement on aura 3a²-7ab+2b²=0
=>(a-2b)(3a-2b)=0
=>a=2b ou 3a=2b
a+b)/(a-b)=3 ou (a+b)/(a-b)=-2 (a-2b)(3a-2b) n'egal pas zero :/ car (a-2b)(3a-2b)= 3a²-8ab+4b² quelle est la relation avec celle décrite en haut ?  bon courage | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Lun 02 Jan 2012, 18:14 Lun 02 Jan 2012, 18:14 | |
| - hind nassri a écrit:
- SLT TT le monde
VOICI mon exercice :
CALCULER :
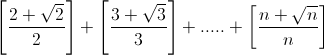
n€N
bonne chance c'est pas difficile je crois ! deja cette somme est equivalente a Sn=n-1+sigma(2->n)[1/Vn] deja pour tout n>1 on a 0<1/Vn<1 alors [1/Vn]=0 ainsi Sn=n-1. - diablo902 a écrit:
- Exercice ??:
Trouvez tous les entiers x,y>0 tels que : x!+3=y² - Spoiler:
Deja on constate que (1,2) et (3,3) sont solutions a cette equation et que pr x=2 l'equation n'admet aucune solution.Et pour tout x>=4 on a x!+3=3[4] et y² est congru a 0 ou 1 modulo 4 ce qui montre la contradiction.
Ainsi les seules solutions de cette equation sont (1,2) et (3,3).
| |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Lun 02 Jan 2012, 18:41 Lun 02 Jan 2012, 18:41 | |
| - yasserito a écrit:
- hind nassri a écrit:
- SLT TT le monde
VOICI mon exercice :
CALCULER :
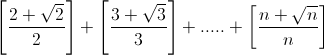
n€N
bonne chance
c'est pas difficile je crois !
deja cette somme est equivalente a Sn=n-1+sigma(2->n)[1/Vn]
deja pour tout n>1 on a 0<1/Vn<1 alors [1/Vn]=0 ainsi Sn=n-1.
- diablo902 a écrit:
- Exercice ??:
Trouvez tous les entiers x,y>0 tels que : x!+3=y²
- Spoiler:
Deja on constate que (1,2) et (3,3) sont solutions a cette equation et que pr x=2 l'equation n'admet aucune solution.Et pour tout x>=4 on a x!+3=3[4] et y² est congru a 0 ou 1 modulo 4 ce qui montre la contradiction.
Ainsi les seules solutions de cette equation sont (1,2) et (3,3).
@yasserito : Est-ce-que 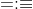 ?
Dernière édition par diablo902 le Lun 02 Jan 2012, 18:43, édité 1 fois | |
|
  | |
hind nassri
Maître

 Nombre de messages : 143 Nombre de messages : 143
Age : 29
Date d'inscription : 25/01/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Lun 02 Jan 2012, 18:42 Lun 02 Jan 2012, 18:42 | |
| - Didou-Touzani a écrit:
- hind nassri a écrit:
- apres developement on aura 3a²-7ab+2b²=0
=>(a-2b)(3a-2b)=0
=>a=2b ou 3a=2b
a+b)/(a-b)=3 ou (a+b)/(a-b)=-2
(a-2b)(3a-2b) n'egal pas zero :/
car
(a-2b)(3a-2b)= 3a²-8ab+4b² quelle est la relation avec celle décrite en haut ? 
bon courage
c'est la factorisation didou touzani | |
|
  | |
hind nassri
Maître

 Nombre de messages : 143 Nombre de messages : 143
Age : 29
Date d'inscription : 25/01/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Lun 02 Jan 2012, 18:47 Lun 02 Jan 2012, 18:47 | |
| - yasserito a écrit:
- hind nassri a écrit:
- SLT TT le monde
VOICI mon exercice :
CALCULER :
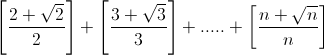
n€N
bonne chance
c'est pas difficile je crois !
deja cette somme est equivalente a Sn=n-1+sigma(2->n)[1/Vn]
deja pour tout n>1 on a 0<1/Vn<1 alors [1/Vn]=0 ainsi Sn=n-1.
- diablo902 a écrit:
- Exercice ??:
Trouvez tous les entiers x,y>0 tels que : x!+3=y²
- Spoiler:
Deja on constate que (1,2) et (3,3) sont solutions a cette equation et que pr x=2 l'equation n'admet aucune solution.Et pour tout x>=4 on a x!+3=3[4] et y² est congru a 0 ou 1 modulo 4 ce qui montre la contradiction.
Ainsi les seules solutions de cette equation sont (1,2) et (3,3).
svp yasserito ecrivez en latex car je n'arrive pas a comprendre votre ecriture sinon laissez les espaces merci d'avance | |
|
  | |
hind nassri
Maître

 Nombre de messages : 143 Nombre de messages : 143
Age : 29
Date d'inscription : 25/01/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Lun 02 Jan 2012, 18:57 Lun 02 Jan 2012, 18:57 | |
| mettez la reponse yasserito si vous la trouverez et merci d'avance | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Lun 02 Jan 2012, 19:03 Lun 02 Jan 2012, 19:03 | |
| - hind nassri a écrit:
- mettez la reponse yasserito si vous la trouverez et merci d'avance
Ses réponses sont justes mais pour comprendre la 2eme il faut changer le signe = par  et étudier l'arithmétique modulaire. On a [img]http://latex.codecogs.com/gif.latex?a\equiv&space;b[n]\Leftrightarrow&space;n|a-b [/img] | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2011-2012 ) |  |
|
