| | Préparations aux olympiades de tronc commun (2011-2012 ) |  |
|
+16hind nassri Didou-Touzani Ahmed Taha (bis) Norax konica ali-mes Mehdi.O Nayssi oiga aminox upsilon salimreda kaj mima Soukaina Amaadour rimetta diablo902 20 participants |
|
| Auteur | Message |
|---|
oiga
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 28
Date d'inscription : 09/11/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Mer 09 Nov 2011, 16:07 Mer 09 Nov 2011, 16:07 | |
| T'as une démonstration pour l'inégalité de Tchebychey? | |
|
  | |
aminox
Maître
 Nombre de messages : 93 Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Mer 09 Nov 2011, 16:42 Mer 09 Nov 2011, 16:42 | |
| Par symétrie on suppose a>=b
donc a^2>=b^2
et 1/(a+1)=<1/(b+1)
D'aprés Tchebychey: a^2/(a+1)+b^2/(b+1) >=1/2 *(a^2+b^2)[1/(a+1)+1/(b+1)] | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Mer 09 Nov 2011, 18:47 Mer 09 Nov 2011, 18:47 | |
| aminox pourquoi tchebychev : Par C.S.: (a+1+b+1)\geq&space;(a+b)^2&space;\newline&space;\Leftrightarrow&space;\frac{a^2}{a+1}+\frac{b^2}{b+1}\geq&space;\frac{1}{2}) J'att vos exercices  | |
|
  | |
aminox
Maître
 Nombre de messages : 93 Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Mer 09 Nov 2011, 20:08 Mer 09 Nov 2011, 20:08 | |
| j'ai pas bien compris la premiére ligne
| |
|
  | |
rimetta
Féru

 Nombre de messages : 57 Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Mer 09 Nov 2011, 20:26 Mer 09 Nov 2011, 20:26 | |
| on fait la différence classique des deux cotés on retrouve donc après nnachr et les simplifications et ta3wid : ab- 1/4 on a : a+b -2Vab >=0 donc 1 -2Vab>=0 d'ou ab <= 1/4 et donc on constate le resultat pour le 12 est ce que n^1/2 = Vn diablo ? voici un exo a et b sont des reels non nuls tel que : 3a - b +2Vab =0 calculez a/b ( I'm finally back  ) | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Mer 09 Nov 2011, 20:37 Mer 09 Nov 2011, 20:37 | |
| Pour l'exo de rimetta "Facile":3a - b +2Vab =0 ^2&space;-(2\sqrt{a})^2=0&space;\newline) AB=0 ==>A=0 ou B=0  La 1er n'a aucune réponse La 2eme donne : 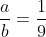 Sauf erreur
Dernière édition par diablo902 le Mer 09 Nov 2011, 20:59, édité 1 fois | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Mer 09 Nov 2011, 20:44 Mer 09 Nov 2011, 20:44 | |
| rimetta:pour le 12 est ce que n^1/2 = Vn diablo ?
OUI et:
[img]http://latex.codecogs.com/gif.latex?2^{\frac{3}{2}}=\sqrt{2^3}~~;~~x^{\frac{1}{n}}=\sqrt[n]{x}[/img] | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Mer 09 Nov 2011, 20:52 Mer 09 Nov 2011, 20:52 | |
| | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Mer 09 Nov 2011, 20:54 Mer 09 Nov 2011, 20:54 | |
| Pour C.S.:
x;y >0
(x²+x'²)(y²+y'²)>=(xy+x'y')² | |
|
  | |
rimetta
Féru

 Nombre de messages : 57 Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Mer 09 Nov 2011, 21:01 Mer 09 Nov 2011, 21:01 | |
| | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Mer 09 Nov 2011, 21:06 Mer 09 Nov 2011, 21:06 | |
| - rimetta a écrit:
- ok merci
Pas de quoi | |
|
  | |
aminox
Maître
 Nombre de messages : 93 Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 11:32 Jeu 10 Nov 2011, 11:32 | |
| Salut,j'ai résolu l'exo de rimetta avec une autre méthode:(Je l'ai résolu dans R*+)
On a: 3a-b+2V(ab)=0
Donc: 3a =b-2V(ab)
<==> 4a=a+b-2V(ab)=(Va+Vb)^2
<==> 4=[1+V(b/a)]^2
<==> V(b/a)=3
<==> b/a=9
On conclue donc que: a/b=1/9 | |
|
  | |
oiga
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 28
Date d'inscription : 09/11/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 16:59 Jeu 10 Nov 2011, 16:59 | |
| Bonjour, voici un nouveau exo
a, b appartiennent à IN
(1+V2)^2006= a+bV2
calculez:
a²+2b²
| |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 17:12 Jeu 10 Nov 2011, 17:12 | |
| (1+V2)²=3+2V2 ; (1+V2)^4=17+12V2 . . . . .(1+V2)^2006= a+bV2
(1-V2)²=3-2V2 ; (1-V2)^4=17-12V2 . . . . .(1-V2)^2006= a-bV2
Donc a²-2b²= (a+bV2)( a-bV2)=1
J'att Vos Exos
Dernière édition par diablo902 le Jeu 10 Nov 2011, 19:25, édité 1 fois | |
|
  | |
aminox
Maître
 Nombre de messages : 93 Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 17:31 Jeu 10 Nov 2011, 17:31 | |
| Pourquoi : a^2+2b^2=(a+bV2)(a-bV2) | |
|
  | |
rimetta
Féru

 Nombre de messages : 57 Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 17:46 Jeu 10 Nov 2011, 17:46 | |
| c'est moins : juste une faute de frappe j'espere
je pense que c'est un exo du manuel de l'année dernière | |
|
  | |
aminox
Maître
 Nombre de messages : 93 Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 18:12 Jeu 10 Nov 2011, 18:12 | |
| nn c pas une faute de frape parce que on veut pas savoir combien égale (a²-2b²) ,on veut savoir (a²+2b²) | |
|
  | |
rimetta
Féru

 Nombre de messages : 57 Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 18:22 Jeu 10 Nov 2011, 18:22 | |
| faute de frappe même f l'énoncé on peut pas CALCULER a^2 +2b^2 | |
|
  | |
oiga
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 28
Date d'inscription : 09/11/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 18:45 Jeu 10 Nov 2011, 18:45 | |
| T'as raison Rimetta, c'est une faute de frappe. Bravo Diablo! c'est très facile | |
|
  | |
rimetta
Féru

 Nombre de messages : 57 Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 18:56 Jeu 10 Nov 2011, 18:56 | |
| voila un ex:
soit a,b,c, et d des reels strictement positifs montrez que
1< a/(a+b+d) +b/(a+b+c) +c/(b+c+d) +d/ (a+c+d) < 2 | |
|
  | |
oiga
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 28
Date d'inscription : 09/11/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 18:58 Jeu 10 Nov 2011, 18:58 | |
| Un autre exo
Montrer que :
1000000000000000000001
N’est pas un nombre premier. | |
|
  | |
rimetta
Féru

 Nombre de messages : 57 Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 19:11 Jeu 10 Nov 2011, 19:11 | |
| ma solution pour l'exo de oiga
on a 1000000000000000000001 = 10^21 +1
= (10^7)^3 +1^3
= (10^7+1)(10^14 + 10^7 + 1)
et donc ce n'est pas un nombre premier | |
|
  | |
oiga
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 28
Date d'inscription : 09/11/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 19:24 Jeu 10 Nov 2011, 19:24 | |
| Bonsoir Rimetta
La réponse
je vais la diviser en deux parties
voici la première partie:
1< a/(a+b+d) +b/(a+b+c) +c/(b+c+d) +d/ (a+c+d) < 2
d'abord on démontre que 1< a/(a+b+d) +b/(a+b+c) +c/(b+c+d) +d/ (a+c+d)
On a a , b , c et d strictement positives
alors
a+b+d<a+b+c+d <==> 1/(a+b+d) > 1/(a+b+c+d) <==> a/(a+b+d) > a/(a+b+c+d)
a+b+c<a+b+c+d <==> 1/(a+b+c) > 1/(a+b+c+d) <==> b/(a+b+c) > b/(a+b+c+d)
b+c+d<a+b+c+d <==> 1/(b+c+d) > 1/(a+b+c+d) <==> c/(b+c+d) > c/(a+b+c+d)
a+c+d<a+b+c+d <==> 1/(a+c+d) > 1/(a+b+c+d) <==> d/(a+c+d) > d/(a+b+c+d)
alors, en faisant la somme des quatres inégalités, on trouve que
a/(a+b+d) +b/(a+b+c) +c/(b+c+d) +d/ (a+c+d) > (a+b+c+d)/(a+b+c+d)
a/(a+b+d) +b/(a+b+c) +c/(b+c+d) +d/ (a+c+d) > 1 | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 19:40 Jeu 10 Nov 2011, 19:40 | |
| La 2eme Partie Je pense qu'il faut utiliser TchebyShev | |
|
  | |
oiga
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 28
Date d'inscription : 09/11/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 19:42 Jeu 10 Nov 2011, 19:42 | |
| La deuxième partie
a/(a+b+d) +b/(a+b+c) = a(a+b+c)+b(a+b+d)/(a+b+c)(a+b+d)
= (a²+ab +ac +ba+b²+bd)/(a²+ab+ad+ba+b²+bd+ca+cb+cd)
= (a²+2ab+ac+bd+b²)/(a²+2ab+ac+bd+b²+ad+cb+cd)
et puisque a, b,c ,c sont strictement positifs
a²+2ab+ac+bd+b²< a²+2ab+ac+bd+b²+ad+cb+cd
alors
(a²+2ab+ac+bd+b²)/(a²+2ab+ac+bd+b²+ad+cb+cd)<1
a/(a+b+d) +b/(a+b+c) <1
Par la même façons on démontre que
c/(b+c+d) +d/ (a+c+d) < 1
et en faisons la somme
a/(a+b+d) +b/(a+b+c) +c/(b+c+d) +d/ (a+c+d) < 2
d'après les deux parties
1< a/(a+b+d) +b/(a+b+c) +c/(b+c+d) +d/ (a+c+d) < 2 | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2011-2012 ) |  |
|
