| | Préparations aux olympiades de tronc commun (2011-2012 ) |  |
|
+16hind nassri Didou-Touzani Ahmed Taha (bis) Norax konica ali-mes Mehdi.O Nayssi oiga aminox upsilon salimreda kaj mima Soukaina Amaadour rimetta diablo902 20 participants |
|
| Auteur | Message |
|---|
oiga
Habitué
 Nombre de messages : 15
Age : 28
Date d'inscription : 09/11/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sam 12 Nov 2011, 14:53 | |
| oui oui aminox quelque soit le triangle
et si j'aurai le temps je vais poster ma réponse | |
|
| | |
aminox
Maître
Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sam 12 Nov 2011, 15:21 | |
| | |
|
| | |
aminox
Maître
Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sam 12 Nov 2011, 15:22 | |
| - diablo902 a écrit:
- Un autre de Géométrie:Svp ne fait pas copier coller du solution dans les sites internet
a,b et c les cotés d'un triangle et p son demi périmetre et S sa surface Prouver que:
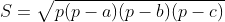 Tu peux me donner le lien ou t'a trouvé cette question | |
|
| | |
diablo902
Maître
Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sam 12 Nov 2011, 15:37 | |
| C'est l'exo d'oiga  | |
|
| | |
aminox
Maître
Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sam 12 Nov 2011, 22:07 | |
| ok | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sam 12 Nov 2011, 23:05 | |
| - Nayssi a écrit:
On considère K et L deux points d’un cercle C de centre O. Soit A un point de la droite (KL)
en dehors du cercle. On note P et Q les points de contact des tangentes à C issues de A. Soit
M le milieu de [P Q]. Montrer que les angles <MKO et <MLO sont égaux
- Spoiler:
 Dans le cercle (C), on a: 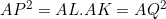 . 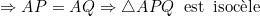 . Et puisque M est le milieu de [PQ], il s'en suit que: %20\perp%20(PQ)\Rightarrow%20\angle%20AMP%20=%20\frac{\pi}{2}) . Et on a: 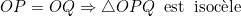 . Et puisque M est le milieu de [PQ], il s'en suit que: %20\perp%20(PQ)\Rightarrow%20\angle%20OMP%20=%20\frac{\pi}{2}) .  Soit (C') le cercle circonscrit au triangle MOP, On a: 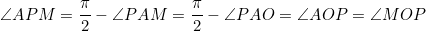 , donc la droite (AP) est tangente à (C') en P. Dans le cercle (C'), on a: 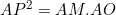 . 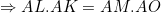 . Donc, d'après la réciperoque de la théorème de la puissance d'un point par rapport à un cercle, le quadrilatère MLKO est inscriptible, d'où:  .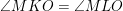
Dernière édition par ali-mes le Dim 13 Nov 2011, 00:05, édité 1 fois | |
|
| | |
diablo902
Maître
Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sam 12 Nov 2011, 23:53 | |
| - ali-mes a écrit:
- Nayssi a écrit:
On considère K et L deux points d’un cercle C de centre O. Soit A un point de la droite (KL)
en dehors du cercle. On note P et Q les points de contact des tangentes à C issues de A. Soit
M le milieu de [P Q]. Montrer que les angles <MKO et <MLO sont égaux
- Spoiler:
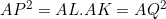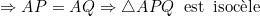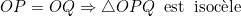Dans le cercle (C), on a: . . Et puisque M est le milieu de [PQ], il s'en suit que: . Et on a: . Et puisque M est le milieu de [PQ], il s'en suit que: .  Soit (C') le cercle circonscrit au triangle MOP, On a: 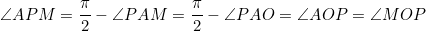, donc la droite (AP) est tangente à (C') en P. Dans le cercle (C'), on a: 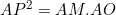. 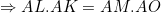. Donc, d'après la réciperoque de la théorème de la puissance d'un point par rapport à un cercle, le quadrilatère MLKO est inscriptible, d'où: .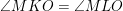
Waw; Bonne Réponse  | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Dim 13 Nov 2011, 00:04 | |
| - diablo902 a écrit:
- ali-mes a écrit:
- Nayssi a écrit:
On considère K et L deux points d’un cercle C de centre O. Soit A un point de la droite (KL)
en dehors du cercle. On note P et Q les points de contact des tangentes à C issues de A. Soit
M le milieu de [P Q]. Montrer que les angles <MKO et <MLO sont égaux
- Spoiler:
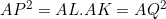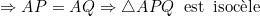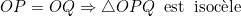Dans le cercle (C), on a: . . Et puisque M est le milieu de [PQ], il s'en suit que: . Et on a: . Et puisque M est le milieu de [PQ], il s'en suit que: . Soit (C') le cercle circonscrit au triangle MOP, On a: 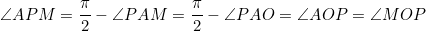, donc la droite (AP) est tangente à (C') en P. Dans le cercle (C'), on a: 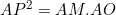. 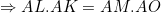. Donc, d'après la réciperoque de la théorème de la puissance d'un point par rapport à un cercle, le quadrilatère MLKO est inscriptible, d'où: .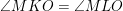
Waw; Bonne Réponse Il y a une petite coquille, c'est plutôt A, O et M qui sont collinéaires  ! je vais éditer ... | |
|
| | |
aminox
Maître
Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Dim 13 Nov 2011, 11:24 | |
| exo 16:
x et y et z trois reéls strictement positives tel que : x+y+z=1
M.Q: (1+1/x)(1+1/y)(1+1/z)>=64
| |
|
| | |
diablo902
Maître
Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Dim 13 Nov 2011, 11:40 | |
| - aminox a écrit:
- exo 16:
x et y et z trois reéls strictement positives tel que : x+y+z=1
M.Q: (1+1/x)(1+1/y)(1+1/z)>=64
P.S.: Je pense qu'il est lexo 27 ;Il faut l’éditer
Dernière édition par diablo902 le Dim 13 Nov 2011, 12:01, édité 1 fois | |
|
| | |
aminox
Maître
Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Dim 13 Nov 2011, 11:55 | |
| - diablo902 a écrit:
- aminox a écrit:
- exo 16:
x et y et z trois reéls strictement positives tel que : x+y+z=1
M.Q: (1+1/x)(1+1/y)(1+1/z)>=64
Je pense qu'il faut utiliser Jensen
P.S.: Je pense qu'il est lexo 27 ;Il faut l’éditer Tu pauex me donner le lien stp | |
|
| | |
diablo902
Maître
Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Dim 13 Nov 2011, 11:57 | |
| Édite le numéro d’abord ; une petite recherche "google" te donne l'inégalité Amicalement  | |
|
| | |
diablo902
Maître
Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Dim 13 Nov 2011, 12:06 | |
| - aminox a écrit:
- diablo902 a écrit:
- aminox a écrit:
- exo 16:
x et y et z trois reéls strictement positives tel que : x+y+z=1
M.Q: (1+1/x)(1+1/y)(1+1/z)>=64
Je pense qu'il faut utiliser Jensen
P.S.: Je pense qu'il est lexo 27 ;Il faut l’éditer
Tu pauex me donner le lien stp Plutôt IAG  si vous voulez je poste la réponse | |
|
| | |
aminox
Maître
Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Dim 13 Nov 2011, 13:05 | |
| | |
|
| | |
diablo902
Maître
Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Dim 13 Nov 2011, 13:50 | |
| Réponse D'exo 27 :- Spoiler:
Dernière édition par diablo902 le Dim 13 Nov 2011, 18:35, édité 1 fois | |
|
| | |
aminox
Maître
Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Dim 13 Nov 2011, 15:16 | |
| | |
|
| | |
konica
Maître
Nombre de messages : 141
Age : 29
Localisation : Tétouan
Date d'inscription : 19/03/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Lun 14 Nov 2011, 17:43 | |
| - diablo902 a écrit:
- Un autre de Géométrie:Svp ne fait pas copier coller du solution dans les sites internet
a,b et c les cotés d'un triangle et p son demi périmetre et S sa surface Prouver que:
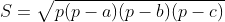Formule de Héron... | |
|
| | |
Norax
Habitué
 Nombre de messages : 16
Age : 28
Date d'inscription : 18/11/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Ven 25 Nov 2011, 17:53 | |
| Salut j'ai pour vous un exercice que je viens de passer en olympiades
x et y et z > 0
montre que
xy/z+yz/x+zx/y>x+y+z | |
|
| | |
Ahmed Taha (bis)
Expert grade2
Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Ven 25 Nov 2011, 18:34 | |
| | |
|
| | |
rimetta
Féru
Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Ven 25 Nov 2011, 20:34 | |
| on a (xy)²+(yz)² >= 2xy²z
(yz)²+(xz)² >= 2xyz²
(xz)²+ (xy)² >= 2x²yz
d'ou (xy)² +(xz)²+(yz)² >= x²yz + xy²z + xyz²
en divisant les deux côtés par xyz tu retrouves plus simplement le resultat | |
|
| | |
rimetta
Féru
Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Dim 27 Nov 2011, 14:48 | |
| exo 28
une montre a deux aiguilles celle des heures et l'autre des minutes, trouvez l'instant où les deux aiguilles seront superposéés entre 2h et 2h et quart
Dernière édition par rimetta le Dim 27 Nov 2011, 14:50, édité 1 fois | |
|
| | |
rimetta
Féru
Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Dim 27 Nov 2011, 14:49 | |
| exo 29
avec une ficelle qui mesure L , indiquez l'hauteur et la largeur d'un rectangle qu'on pourrait faire avec telle que sa surface soit maximale | |
|
| | |
Didou-Touzani
Habitué
Nombre de messages : 20
Age : 29
Localisation : Casablanca
Date d'inscription : 31/12/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Dim 01 Jan 2012, 16:43 | |
| salut tout le monde rimetta je vais essayer de résoudre tes 2 problems en attendant je pose un exercice a,b,c des réels positifs tel que a+b+c=1 M.Q: (1-a)(1-b) plus petit ou egal à [(1+c)/2]² P.Q: (1-a)(1-b)(1-c) plus petit ou egal à 1/2 bonne chance les matheux  | |
|
| | |
Ahmed Taha (bis)
Expert grade2
Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Dim 01 Jan 2012, 17:53 | |
| | |
|
| | |
Didou-Touzani
Habitué
Nombre de messages : 20
Age : 29
Localisation : Casablanca
Date d'inscription : 31/12/2011
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Dim 01 Jan 2012, 17:59 | |
| bravo abdelkrim allez posez nous des exos ! pas nécessairement d'inégalités | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) | |
| |
|
| | |
| | Préparations aux olympiades de tronc commun (2011-2012 ) | |
|
