| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
+46Norax Mehdi-el redouaneamraouza Misterayyoub diablo902 *youness* Loliiiita kaj mima ilyasaitazzi l'intellectuelle az360 konica darkpseudo Mehdi.O maths_lady mathadores amigo-6 K-maths youpi alumenne.b achraf_djy boubou math yumi M.Marjani Nayssi Meded louis yasserito master Othmaann houssa ayoubmath nmo Dijkschneier mizmaz belkhayaty Azerty1995 tarask Hamouda anas-az_137 matheux-xman Ahmed Taha (bis) maths-au-feminin A446 supista ali-mes 50 participants |
|
| Auteur | Message |
|---|
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Préparations aux olympiades de tronc commun (2010-2011)  Lun 06 Déc 2010, 11:36 Lun 06 Déc 2010, 11:36 | |
| j'ai l'honneur de vous annoncer le début d'un nouveau jeu dans le but de préparer les olympiades de cette année. les conditions de participer sont très simples: 1)- poster le problème en indiquant son numéro. 2)- celui qui a trouvé la réponse, il doit poster un autre problème. Mais si la solution n'est pas trouvée pendant 48 heure, celui qui a posté le problème doit poster une réponse. 3)- on est tous ici pour apprendre, donc, les taupins n'hésitez pas à nous enrichir avec vos suggestions et conseilles. 4)- si quelqu'un postera un problème qui existe déjà dans le forum. il est préférable de poster le lien dans-lequel on peut trouver la réponse. Enfin, je vous propose ces 2 exos: Problème 1:a, b et c trois nombres réels strictement positifs tel que a =< b =< c M.Q: 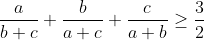 Problème 2: Problème 2:soient x, y et z trois réels strictement positifs tel que: x+y+z=1. M.Q: 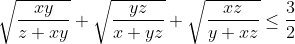 | |
|
  | |
supista
Féru
 Nombre de messages : 39 Nombre de messages : 39
Age : 34
Date d'inscription : 05/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 06 Déc 2010, 21:02 Lun 06 Déc 2010, 21:02 | |
| bsr!! je commence  pour le problème 1 pas besoin d'ajouter la condition sur a,b et c puisque l'inégalité est symétrique. voila la solution de toute façon: poser x=b+c , y=a+c et z=a+b alors remarquer que :y+z=2a+z et ainsi de suite Donc si on pose le membre de gauche S on aura 2S+3=(y+z)/x+(z+x)/y+(x+y)/z=(y/x+x/y)+(y/z+z/y)+(z/x+x/z) >= 2+2+2=6 D'ou l'négalité  | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 06 Déc 2010, 21:40 Lun 06 Déc 2010, 21:40 | |
| voila ma méthode pour le 1er problème: on a 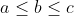 d'où 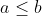 et 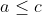 alors 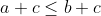 et 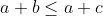 d'où 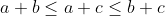 alors 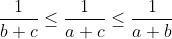 d'après l'inégalité de Chebyshev on a donc \left%20(%20\frac{1}{b+c}%20+%20\frac{1}{a+c}%20+%20\frac{1}{a+b}%20\right%20)\leq%20\frac{a}{b+c}%20\right%20+\frac{b}{a+c}+%20\frac{c}{a+b}%20\right%20\right%20)) donc \leq%20\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}) d'où le résultat 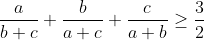 CQFD
Dernière édition par ali-mes le Lun 06 Déc 2010, 21:43, édité 1 fois | |
|
  | |
supista
Féru
 Nombre de messages : 39 Nombre de messages : 39
Age : 34
Date d'inscription : 05/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 06 Déc 2010, 21:42 Lun 06 Déc 2010, 21:42 | |
| c'est bien, mais j'ai pas encore fini  je continue pour le problème 2 remarquer que: z+xy=z(x+y+z)+xy=(z+x)(z+y) donc racine(xy/z+xy)=racine(xy/(z+x)(z+y) <=1/2(z/(z+x)+z/(z+y)) et on fait la mm chose pour les autre termes, on obtient l'inégalité en sommant. c'est à mon tour maintenant de poser un probleme et cette fois ça ne sera pas une inégalité, mais un exercice pas facile en arithmétique, mais de solution très courte, alors essayer de vos mieux pour trouver une solution: voila le problème trouver toutes les solutions dans N*xN*xN* de l'équation: 4xy-x-y=z^2 | |
|
  | |
A446
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 28
Date d'inscription : 23/04/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 12:40 Mar 07 Déc 2010, 12:40 | |
| exo :
on donne: An=1/(rac(n).(n+1)+n.rac(n+1)) (n en indice)
calculez:
S=A1+A2+A3+A4+A5+A6+........+A99
P.S:désolé, je ne maitrise pas Latex xD. | |
|
  | |
supista
Féru
 Nombre de messages : 39 Nombre de messages : 39
Age : 34
Date d'inscription : 05/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 12:43 Mar 07 Déc 2010, 12:43 | |
| mais il faut répondre à l'exo posé d'abord, il faut respecter les règles du jeux  (pour ton exercice,c'est une somme télescopique ) | |
|
  | |
A446
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 28
Date d'inscription : 23/04/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 12:49 Mar 07 Déc 2010, 12:49 | |
| voila sa vient: voila les données http://latex.codecogs.com/gif.latex?a_{n}=\frac{1}{(n+1)\sqrt{n}+n\sqrt{n+1}} et calculez S (1,2,3,4,5..... sont en indice  ) bonne chance | |
|
  | |
A446
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 28
Date d'inscription : 23/04/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 12:51 Mar 07 Déc 2010, 12:51 | |
| ah dezo ^^
jgo essaye, j'ai po vu | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 13:38 Mar 07 Déc 2010, 13:38 | |
| supista a raison il faut d'abord répondre au problème qu'il a posté  | |
|
  | |
A446
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 28
Date d'inscription : 23/04/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 15:00 Mar 07 Déc 2010, 15:00 | |
| la reponse est: il n'y a pas de solution (x,y,z) dans NxNxN .
pour la démonstration je la met dans quelques instants . | |
|
  | |
A446
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 28
Date d'inscription : 23/04/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 15:23 Mar 07 Déc 2010, 15:23 | |
| je crois qu'il faut au moin ZxZxZ pour pouvoir écrir 4xy-x-y en forme de carré complet non??  | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 15:30 Mar 07 Déc 2010, 15:30 | |
| ??????????????????  | |
|
  | |
supista
Féru
 Nombre de messages : 39 Nombre de messages : 39
Age : 34
Date d'inscription : 05/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 15:32 Mar 07 Déc 2010, 15:32 | |
| bah je peux t'affirmer qu'il n'y a pas de solution si les variables sont des entiers positifs, j'ai une solution qui ne fait pas intervenir des inégalités ou des raisonnements genre analytique, mais que de l'arithmétique élémentaire et des manipulations algébriques
Dernière édition par supista le Mar 07 Déc 2010, 15:40, édité 1 fois | |
|
  | |
maths-au-feminin
Maître
 Nombre de messages : 70 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 15:35 Mar 07 Déc 2010, 15:35 | |
| j'ai deux question pour vous klk1 ki pe me dire c koi l'inégualité de Chebyshev et klk1 ki peut me donner une solution détaillée pour le 2eme probleme ...... | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 15:41 Mar 07 Déc 2010, 15:41 | |
| l'inégalité de Chebyshev: Soit 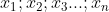 et 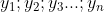 des réels strictement positifs. tel que 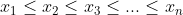 et 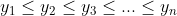 d'après l'inégalité de Chebyshev on a (y_{1}+y_{2}+y_{3}+...+y_{n})\leq%20n(x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}+...+x_{n}y_{n}))
Dernière édition par ali-mes le Mar 07 Déc 2010, 15:58, édité 1 fois | |
|
  | |
A446
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 28
Date d'inscription : 23/04/2010
 | |
  | |
supista
Féru
 Nombre de messages : 39 Nombre de messages : 39
Age : 34
Date d'inscription : 05/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 15:49 Mar 07 Déc 2010, 15:49 | |
| je vais attendre jusqu'à cette nuit, si personne ne peux parvenir à trouver une solution, je vais poster ma solution incha2alah, avec un autre problème  , je vous laisse essayer j'ai maintenant un cours, bonne chance | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 15:52 Mar 07 Déc 2010, 15:52 | |
| ma méthode pour le 2eme problème: on a z+xy=z(x+y+z)+xy=xz+yz+z²+xy=(x+z)(y+z) d'où (y+z)}) et d'après IAG on a: (y+z)}\leq%20\frac{1}{2}\left%20(%20\frac{x}{x+z}+\frac{y}{y+z}%20\right%20)) de la même façon on démontre que ) et ) en sommant en trouve que 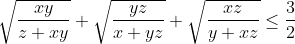 | |
|
  | |
A446
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 28
Date d'inscription : 23/04/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 15:52 Mar 07 Déc 2010, 15:52 | |
| thx, on essayera  | |
|
  | |
maths-au-feminin
Maître
 Nombre de messages : 70 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 15:54 Mar 07 Déc 2010, 15:54 | |
| | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 15:59 Mar 07 Déc 2010, 15:59 | |
| j'ai édité le 1er message ==== (faute d'inattention)  | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 18:19 Mar 07 Déc 2010, 18:19 | |
| - A446 a écrit:
- exo :
on donne: An=1/(rac(n).(n+1)+n.rac(n+1)) (n en indice)
calculez:
S=A1+A2+A3+A4+A5+A6+........+A99
P.S:désolé, je ne maitrise pas Latex xD. An=1/(rac(n).(n+1)+n.rac(n+1)) (n en indice) An=(rac(n).(n+1)-n.(n+1))/((n).(n+1)²-n^2.(n+1)) =(rac(n).(n+1)-n.rac(n+1))/n(n+1) =1/rac(n) - 1/rac(n+1) A1 = 1 - 1/rac(2) A2 = 1/rac(2) - 1/rac(3) . . . A99 = 1/rac(99) - 1/10 donc S = 1 - 1/10 = 9/10 | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 18:37 Mar 07 Déc 2010, 18:37 | |
| l'exo que A446 est facile. celui de soupista est un peu compliqué !!! | |
|
  | |
A446
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 28
Date d'inscription : 23/04/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 18:51 Mar 07 Déc 2010, 18:51 | |
| d'après mes recherces c'est une equation diophantine , mais aprés plusieurs modulations je n'ai toujours pas trouvé une solution arithmétique  | |
|
  | |
A446
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 28
Date d'inscription : 23/04/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 07 Déc 2010, 19:04 Mar 07 Déc 2010, 19:04 | |
| - abdelkrim-amine a écrit:
- A446 a écrit:
- exo :
on donne: An=1/(rac(n).(n+1)+n.rac(n+1)) (n en indice)
calculez:
S=A1+A2+A3+A4+A5+A6+........+A99
P.S:désolé, je ne maitrise pas Latex xD.
An=1/(rac(n).(n+1)+n.rac(n+1)) (n en indice)
An=(rac(n).(n+1)-n.(n+1))/((n).(n+1)²-n^2.(n+1))
=(rac(n).(n+1)-n.rac(n+1))/n(n+1)
=1/rac(n) - 1/rac(n+1)
A1 = 1 - 1/rac(2)
A2 = 1/rac(2) - 1/rac(3)
.
.
.
A99 = 1/rac(99) - 1/10
donc S = 1 - 1/10 = 9/10 jolie coup, c'est bon  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
