| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
+46Norax Mehdi-el redouaneamraouza Misterayyoub diablo902 *youness* Loliiiita kaj mima ilyasaitazzi l'intellectuelle az360 konica darkpseudo Mehdi.O maths_lady mathadores amigo-6 K-maths youpi alumenne.b achraf_djy boubou math yumi M.Marjani Nayssi Meded louis yasserito master Othmaann houssa ayoubmath nmo Dijkschneier mizmaz belkhayaty Azerty1995 tarask Hamouda anas-az_137 matheux-xman Ahmed Taha (bis) maths-au-feminin A446 supista ali-mes 50 participants |
|
| Auteur | Message |
|---|
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 09 Déc 2010, 12:56 Jeu 09 Déc 2010, 12:56 | |
| - abdelkrim-amine a écrit:
- Azerty1995 a écrit:
- Salut
Probleme 7
Definir a et b de IR tel que
3V(a-9)+5V(b-25)=(a+b)/2
Bonne chance
je ne comprend pas votre "V", est ce que tu peux réecrire ton énoncé  Salut 'V' veut dire racine. | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 09 Déc 2010, 15:40 Jeu 09 Déc 2010, 15:40 | |
| Voici un autre
Problème 8
Montrez que pour tout n de IN*-{1,2}
(n+1)^n < n^(n+1)
Bonne chance | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Sam 11 Déc 2010, 10:48 Sam 11 Déc 2010, 10:48 | |
| salut azerty1995 peux tu nous poster la reponse pour le 7eme et 8eme problemes !!!!! et merci d'avance !!!  | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Sam 11 Déc 2010, 15:03 Sam 11 Déc 2010, 15:03 | |
| J'ai pas la solution, voici un autre problème pour faire marcher le jeu en attendant que quelqu'un poste une réponse
Probleme 9
Montrez que pour tout réel strictement positif a,b et c on a
(a+b+c)(1/a +1/b+1/c)>= 9
Bonne chance
| |
|
  | |
belkhayaty
Féru
 Nombre de messages : 68 Nombre de messages : 68
Age : 30
Date d'inscription : 30/11/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Sam 11 Déc 2010, 16:11 Sam 11 Déc 2010, 16:11 | |
| ce n'est pas une application directe de l'inegalité de cauchy-shwarz ?
( a + b + c ) ( 1/a + 1/b + 1/c)>= ( a x 1/a + b x 1/b + c x 1/c)²
>= (1 + 1 + 1 )²
>= 9
| |
|
  | |
Hamouda
Maître
 Nombre de messages : 125 Nombre de messages : 125
Age : 30
Date d'inscription : 26/11/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Sam 11 Déc 2010, 16:54 Sam 11 Déc 2010, 16:54 | |
| c vrai pas pas à 100% xD
le résultat est le même mais c'est plutot sqrt(a)*1/sqrt(a) ^^ | |
|
  | |
Hamouda
Maître
 Nombre de messages : 125 Nombre de messages : 125
Age : 30
Date d'inscription : 26/11/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Sam 11 Déc 2010, 17:39 Sam 11 Déc 2010, 17:39 | |
| je pense que la réponse de belkhayaty est juste (sauf la petite faute que j'ai corrigée), donc pour ne pas retarder le jeu je poste 1 prob:
Probleme 10
Trouver les triplets x, y et z de N* tel que:
x^2 + y^2 + 2xy - z^2 = 9
Bonne chance. | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 12 Déc 2010, 16:22 Dim 12 Déc 2010, 16:22 | |
| voila ma méthode:
x²+y²+2xy-z²=9
(x²+2xy+y²)-z²=9
(x+y)²-z²=9
(x+y+z)(x+y-z)=9
on a (x;y;z)£IN*
et x+y+z>x+y-z
donc x+y+z=9
et x+y-z=1
d'où x+y=5 et z=4
donc x=1 et y=4
ou x=2 et y=3
ou x=3 et y=2
ou x=4 et y=1
conclusion:
S={(1;4;4)/(2;3;4)/(3;2;4)/(4;1;4)}
| |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 12 Déc 2010, 16:58 Dim 12 Déc 2010, 16:58 | |
| pour ne pas retarder le jeu je vais poster ces deux exos: le premier un peu facile mais le deuxieme est compliqué un peu. problème 11:x; y; z; a; b; et c des nombres strictement positifs tel que:  M.Q:  problème 12: problème 12:considérons un triangle ABC. P un point inscrit dans ce triangle. (AP) et (BP) et (CP) coupent (BC) et (AC) et (AB) respectivement dans D et E et F. M.Q: 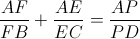 | |
|
  | |
maths-au-feminin
Maître
 Nombre de messages : 70 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 12 Déc 2010, 18:25 Dim 12 Déc 2010, 18:25 | |
| posons x/a=y/b=z/c=m
x=ma
y=mb
z=mc
donc
ax=ma^2
by=mb^2
cz=mc^2
Vax=aVm
Vby=bVm
Vcz=cVm
la somme V(ax+by+cz)=(a+b+c)Vm
et on a (x+y+z)/(a+b+c)=m
et V(a+b+c)(x+y+z)=V(a+b+c)^2,
=(a+b+c)Vm
d'où V(ax+by+cz)=V(a+b+c)(x+y+z) | |
|
  | |
maths-au-feminin
Maître
 Nombre de messages : 70 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 12 Déc 2010, 18:29 Dim 12 Déc 2010, 18:29 | |
| pour probleme 12 -_-_-_-_-_-_-_-_-_-_-_-_-_-_-despasse mon niveau en attente k kelk1 poste la reponse | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 12 Déc 2010, 18:34 Dim 12 Déc 2010, 18:34 | |
| bien joué maths-au-feminin !!  et pour l'exo de géometrie il faut juste utiliser Thalès | |
|
  | |
maths-au-feminin
Maître
 Nombre de messages : 70 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 14 Déc 2010, 18:47 Mar 14 Déc 2010, 18:47 | |
| efin; je l'ai résolu !!!!  considérons D' la projection de D sur (AC) en par. avec (BE) et D" la projection de D sur (AB) en par. avec (CF) dans le triangle ADD' on a (PE)ll(DD') donc d'après Thalès on a AP/PD=AE/ED':(1) dans le triangle ADD" on a (FP)ll(DD") donc AP/PD=AF/FD'' donc AP/PD=AE/ED'=AF/FD" dans le triangle BCE on a (DD')ll(BE) donc ED'/EC=BD/BC donc ED'=(EC.BD)/BC:(2)dans le triangle BCF on a (CF)ll(DD'') donc FD"/FB=CD/CB donc FD"=(FB.CD)/BC:(3) de 1 et 2 et 3 on conclut que c a klk1 d'autre de terminer car il y a des fractions et je ne sais pas commnt utiliser LATEX !!!!!!!!!!!  je posterai mon exo après  | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 14 Déc 2010, 19:07 Mar 14 Déc 2010, 19:07 | |
| super maths-au-feminin ! je vais terminer la méthode que maths-au-feminina posté (c sa methode) 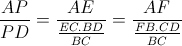 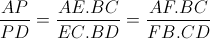 signifie que 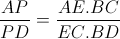 et 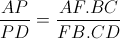 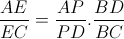 et 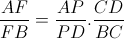 d'où 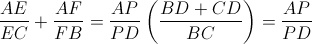 amicalement | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 14 Déc 2010, 19:11 Mar 14 Déc 2010, 19:11 | |
| En attendant que quelqu'un poste un exercice. | |
|
  | |
supista
Féru
 Nombre de messages : 39 Nombre de messages : 39
Age : 34
Date d'inscription : 05/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 14 Déc 2010, 19:29 Mar 14 Déc 2010, 19:29 | |
| c'est un exercice classique, pas difficile, mais très intérressant:
Probleme 13
On choisit n+1 entiers dans l'ensemble {1,..,2n-1} (n>0) ,montrer qu'on peut trouver trouver parmi ces n+1 entiers deux entier a et b tel que a divise b. | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 14 Déc 2010, 20:33 Mar 14 Déc 2010, 20:33 | |
| Salut Est ce que quelqu'un a une idée sur les problèmes 7 et 8,j'aimerais bien avoir des réponses , je n'arrive pas à les résoudre je demande votre aide Merci d'avance  | |
|
  | |
maths-au-feminin
Maître
 Nombre de messages : 70 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mer 15 Déc 2010, 12:27 Mer 15 Déc 2010, 12:27 | |
| je vais poster mon exo: trouve toutes les polynômes P(x) tel que deg(P(x))=2 et P(x-1)+P(x)=x puis conclut la somme 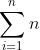 ~~~ j'ai appris a écrire en latex avec l'aide de ce lien http://www.codecogs.com/components/eqneditor/editor.php  j'ai pas pu résoudre l'exo de supista ~ dépasse notre niveau (a mon avis) | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mer 15 Déc 2010, 13:02 Mer 15 Déc 2010, 13:02 | |
| Salam, pour l'exo que supista a proposé je l'ai donné à notre prof. de maths. et il me l'as résolu avec l'utilisation de quelque choses hors de notre programme. Et pour l'exo de maths-au-feminin je crois que j'ai déjà vu cet exercice dans dima dima mais j'ai une petite remarque: il fallait écrire 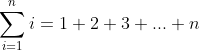 pas 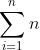 en tous cas voila la réponse on a d°P(x)=2 donc P(x) s'écrit sous la forme de P(x)=ax²+bx+c (a £ IR* ) d'où P(x+1)=a(x+1)²+b(x+1)+c P(x+1)=a(x²+2x+1)+bx+b+c P(x+1)=ax²+2ax+a+2a+bx+b+c P(x+1)=(ax²+bx+c)+2ax+a+b P(x+1)=P(x)+2ax+a+b donc P(x+1)-P(x)=2ax+a+b d'où 2ax+b=x alors a=1/2 et b=-1/2 et c={IR} d'où P(x)=1/2.x²-1/2.x+c (c £ IR) prenons c=0 donc on a pour tous x£IR P(x-1)+P(x)=1 on posons x=1 et x=2 puis x=3 ............... puis x=n-1 puis x=n la somme de ces nombres donne: 1+2+3+......+n-1+n=[P(2)-P(1)]+[P(3)-P(2)]+[P(4)-P(3)]+........+[P(n)-P(n-1)]+[P(n+1)-P(n)] donc 1+2+3+...+n=P(n+1)-P(1) 1+2+3+...+n=n(n+1)/2 d'où la somme i de i=1 à i=n est égale à le produit de n et n+1 divisé par 2
Dernière édition par ali-mes le Jeu 16 Déc 2010, 22:53, édité 1 fois | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mer 15 Déc 2010, 13:07 Mer 15 Déc 2010, 13:07 | |
| en attendant que quelqu'un poste la réponse pour le problème de supista à condition qu'elle soit simplifié et compréhensible pour nous -les TCéans (un mot que j'ai inventé  )- P.S: pour ceux qui ne sont pas habitué avec SIGMA voilà un lien très utile http://homeomath.imingo.net/sigma.htm | |
|
  | |
supista
Féru
 Nombre de messages : 39 Nombre de messages : 39
Age : 34
Date d'inscription : 05/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mer 15 Déc 2010, 20:06 Mer 15 Déc 2010, 20:06 | |
| | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mer 15 Déc 2010, 21:48 Mer 15 Déc 2010, 21:48 | |
| waww ! la méthode que supoista a proposé est fascinante est plus compréhensible que celle mon prof (le connard  ) m'a donné. big THUMB-UP 4 u bon, je vais poster deux problèmes (les deux sont tirés de quelques olymp. de TC) problème14:considérons la polynôme =x^{100}-36x^{98}+16x^{96}+2005) calcule ) problème15: problème15:trouves toutes les entiers naturels tel que: 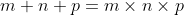 | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 | |
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 16 Déc 2010, 22:55 Jeu 16 Déc 2010, 22:55 | |
| tu as raison azerty1995 c plutôt 2ax+a+b=x pas 2ax+a=0 on résous le système 2a=1 et a+b=0 (c clair)  AMICALEMENT | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 16 Déc 2010, 22:55 Jeu 16 Déc 2010, 22:55 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
