| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
+46Norax Mehdi-el redouaneamraouza Misterayyoub diablo902 *youness* Loliiiita kaj mima ilyasaitazzi l'intellectuelle az360 konica darkpseudo Mehdi.O maths_lady mathadores amigo-6 K-maths youpi alumenne.b achraf_djy boubou math yumi M.Marjani Nayssi Meded louis yasserito master Othmaann houssa ayoubmath nmo Dijkschneier mizmaz belkhayaty Azerty1995 tarask Hamouda anas-az_137 matheux-xman Ahmed Taha (bis) maths-au-feminin A446 supista ali-mes 50 participants |
|
| Auteur | Message |
|---|
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 29 Mar 2012, 19:02 Jeu 29 Mar 2012, 19:02 | |
| si x=y , d’après la condition x=0 l'inégalité est vérifier . si x différent de y , il suffit de remarque que (x-y)(x²+4y²) < x^3+y^3 , car ceci est équivalent a : 4y²x-yx² - 5y^3=-y(y²+(2y-x)²) < 0 d'ou le résultat d’après la condition . | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 29 Mar 2012, 20:05 Jeu 29 Mar 2012, 20:05 | |
| Problème 98 : a,b,c > 0 tel que : abc=1 . Prouver que : (b+1)}+\frac{b}{(b+1)(c+1)}+\frac{c}{(c+1)(a+1)}\geq{\frac{3}{4}}) | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 29 Mar 2012, 20:18 Jeu 29 Mar 2012, 20:18 | |
| - Oty a écrit:
- Problème 98 : a,b,c > 0 tel que : abc=1 . Prouver que :
(b+1)}+\frac{b}{(b+1)(c+1)}+\frac{c}{(c+1)(a+1)}\geq{\frac{3}{4}}) l'inégalité est équivalente à }{\prod%20(c+1)}%20\ge%20\frac{3}{4}) ou bien  une application directe d'IAG  | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 29 Mar 2012, 21:12 Jeu 29 Mar 2012, 21:12 | |
| oui bravo  . | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 29 Mar 2012, 21:19 Jeu 29 Mar 2012, 21:19 | |
| Problème 99:Salut, 
Dernière édition par diablo902 le Jeu 29 Mar 2012, 23:18, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 29 Mar 2012, 22:17 Jeu 29 Mar 2012, 22:17 | |
| - Oty a écrit:
- si x=y , d’après la condition x=0 l'inégalité est vérifier . si x différent de y , il suffit de remarque que (x-y)(x²+4y²) < x^3+y^3 , car ceci est équivalent a : 4y²x-yx² - 5y^3=-y(y²+(2y-x)²) < 0 d'ou le résultat d’après la condition .
Sans mentir, je n'ai jamais vu une telle solution. Bravo. Cependant, ta solution manque de précision: Tu dois démontrer que x est supérieur ou égal à y, ce qui est trivial depuis l'hypothèse. Ensuite, l'inégalité à prouver doit être large: En effet, le couple (1,0) mène vers une égalité. Au plaisir! | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 29 Mar 2012, 23:35 Jeu 29 Mar 2012, 23:35 | |
| on pose : a=max(a,b,c) , l'inégalité est équivalente a : a(b-c)²(b+c-a)+b(a-b)(a-c)(a+b-c) >=0 ce qui vrai d’après l'inégalité triangulaire . | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 29 Mar 2012, 23:52 Jeu 29 Mar 2012, 23:52 | |
| Problème 100 7adide jami3e azwaje (a,b) min z² bi7ayte : 2ab=a+b+4 . | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 30 Mar 2012, 00:24 Ven 30 Mar 2012, 00:24 | |
| Merci nmo  . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 15 Avr 2012, 12:12 Dim 15 Avr 2012, 12:12 | |
| - Oty a écrit:
- Problème 100 7adide jami3e azwaje (a,b) min z² bi7ayte : 2ab=a+b+4 .
Je propose une solution, même si l'exercice est facile: L'équation proposée équivaut à (2a-1)(2b-1)=4ab-2a-2b+1=2(2ab-a-b)+1=2*4+1=9. Comme les diviseurs de 9 sont -1, -3, -9, 1, 3, 9 on doit étudier un tas de cas. On peut réduire ces cas en remarquant la symétrie du problème: _Si 2a-1=-1 et 2b-1=-9, alors a=0 et b=-4. _Si 2a-1=-3 et 2b-1=-3, alors a=-1 et b=-1. _Si 2a-1=1 et 2b-1=9, alors a=1 et b=5. _Si 2a-1=3 et 2b-1=3, alors a=2 et b=2. Il s'ensuit que les couples solutions sont (0,4); (4,0); (1,5); (5,1); (-1,-1) et (2,2). Sauf erreurs. | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 15 Avr 2012, 12:23 Dim 15 Avr 2012, 12:23 | |
| probleme 101 :ABCD inscriptible et les deux bissectrice de DBC et DAC se coupet en L . montrer que : L appartenant au cercle circonscrit du triangle ABC .  | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 15 Avr 2012, 15:52 Dim 15 Avr 2012, 15:52 | |
| Solution au Problème 101: - Spoiler:
Lemme: Soit ABC un triangle, et I le centre de son cercle inscrit, D la deuxième intersection de la bissectrice intérieure de l'angle 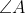 avec le cercle circonscrit au triangle ABC, est le centre du cercle circonscrit au triangle BIC. Preuve:  On a: 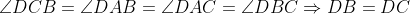 Et on a: 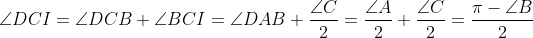 Et: 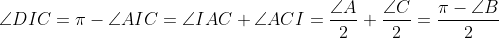 Donc: 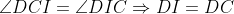 . Il s'en suit que D est le centre du cercle circonscrit au triangle BIC. Revenons au problème initial:  Soit I_a le centre du cercle inscrit au triangle BCD, et L_a la deuxième intersection de la bissectrice intérieure de angle{DBC} avec le cercle circonscrit au quadrilatère ABCD. On définit de la même manière les points I_b et L_b. D'après le lemme, L_a est le centre du cercle circonscrit au triangle CDI_a, donc L_a appartient au médiatrice du segment [CD] et l'arc (CD) du cercle (ABCD) ne contenant pas B. De même, on trouve que L_b est le centre du cercle circonscrit au triangle CDI_b, donc L_b appartient au médiatrice du segment [CD] et l'arc (CD) du cercle (ABCD) ne contenant pas A. Donc: L_a=L_b , et le résultat en découle...
Problème 102: Soient a,b et c des réels positifs. Montrer que: ^2%20+%20b(b-c)^2%20\geq%20(a%20-%20c)(b%20-%20c)(a+b-c)) | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 15 Avr 2012, 16:38 Dim 15 Avr 2012, 16:38 | |
| @ Ali: ce lemme" Soit ABC un triangle, la deuxième intersection de la bissectrice intérieure de l'angle A avec le cercle circonscrit au triangle ABC est le milieu de l'arc BC" est suffisant pour conclure dans quelques lignes  ! Solution au problème 102:l'inégalité est équivalente à ) ce qui est une application directe de Schur! (n=1) Je n'ai pas de problème à proposer | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 15 Avr 2012, 17:25 Dim 15 Avr 2012, 17:25 | |
| - diablo902 a écrit:
- @ Ali: ce lemme"Soit ABC un triangle, la deuxième intersection de la bissectrice intérieure de l'angle A avec le cercle circonscrit au triangle ABC est le milieu de l'arc BC" est suffisant pour conclure dans quelques lignes
 ! !
Hein !? Je ne vois pas l'utilité de ce commentaire, puisque c'est presque la même chose que j'ai fait !
Dernière édition par ali-mes le Dim 15 Avr 2012, 22:24, édité 1 fois | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 15 Avr 2012, 18:12 Dim 15 Avr 2012, 18:12 | |
| ma solution de my own (mybie) probleme 101
notant : L et l'intersection du deux bissectrices
on a : DBC = DAC alors LBC = LAC et ca implique que : LCBA est inscriptibles d'ou le resultat !! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 19 Avr 2012, 20:39 Jeu 19 Avr 2012, 20:39 | |
| Problème 103:Soient x, y et z des réels strictement positifs. Montrez que: .\frac{x+y}{y+z}+(2y-z-x).\frac{y+z}{z+x}+(2z-x-y).\frac{z+x}{x+y}\geq0) . Bonne chance. | |
|
  | |
Siba
Maître

 Nombre de messages : 143 Nombre de messages : 143
Date d'inscription : 12/12/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 20 Avr 2012, 01:14 Ven 20 Avr 2012, 01:14 | |
|
Dernière édition par Siba le Ven 20 Avr 2012, 10:11, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 20 Avr 2012, 02:07 Ven 20 Avr 2012, 02:07 | |
| J'ai deux reproches à te faire: _Je ne comprends pas bien le passage suivant: - Siba a écrit:
- <==> ax -bx +by -cy +cz -az >0
<==> (a-b)x/b + (b-c)y/c + (c-a)z/a > 0 _Je ne comprends pas pourquoi tu travailles avec une inégalité stricte? | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 20 Avr 2012, 15:35 Ven 20 Avr 2012, 15:35 | |
| Probleme 103 :one line solution 1 : \frac{x+y}{y+z}%20=%20\frac{2(x+y+z)(\sum%20x^3%20-%20\sum%20xy^{2})}{\prod%20(x+y)}) (c'est claire Am-Gm) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 23 Avr 2012, 18:06 Lun 23 Avr 2012, 18:06 | |
| - az360 a écrit:
- Probleme 103 :
one line solution 1 : \frac{x+y}{y+z}%20=%20\frac{2(x+y+z)(\sum%20x^3%20-%20\sum%20xy^{2})}{\prod%20(x+y)}) (c'est claire Am-Gm) (c'est claire Am-Gm) Je n'ai pas vérifié la factorisation que tu as cité, mais à part ça: si elle est juste, alors démontrer que  est positif découle de l'inégalité du réordonnement. Sinon, je propose une solution d'un certain marocain qui fait preuve d'une beauté incomparable (extraite de "art of problem solving"): On procède par équivalences successives: On a .\frac{x+y}{y+z}+(2y-z-x).\frac{y+z}{z+x}+(2z-x-y).\frac{z+x}{x+y}\geq0) . Donc -x-y+2y.\bigg(\frac{y+z}{z+x}\bigg)-y-z+2z.\bigg(\frac{z+x}{x+y}\bigg)-z-x\geq0) . Ou encore +2y.\bigg(\frac{y+z}{z+x}\bigg)+2z.\bigg(\frac{z+x}{x+y}\bigg)\geq2x+2y+2z) . Donc +y.\bigg(\frac{y+z}{z+x}\bigg)+z.\bigg(\frac{z+x}{x+y}\bigg)\geq x+y+z) . Donc  . Donc  . Donc +y.\bigg(\frac{y}{z+x}+\frac{x}{y+z}\bigg)+z.\bigg(\frac{z}{x+y}+\frac{y}{z+x}\bigg)\geq x+y+z) . Donc +y.\bigg(\frac{y}{z+x}+1+\frac{x}{y+z}+1\bigg)+z.\bigg(\frac{z}{x+y}+1+\frac{x}{z+x}+1\bigg)\geq 3(x+y+z)) . Et ainsi +y.\bigg(\frac{x+y+z}{z+x}+\frac{x+y+z}{y+z}\bigg)+z.\bigg(\frac{x+y+z}{x+y}+\frac{x+y+z}{z+x}\bigg)\geq 3(x+y+z)) . Soit en réduisant  . Et finalement  . Ce qui est l'inégalité arithmético-géométrique. (Voici de quoi je parle: ^{\frac{1}{3}}=3\times 1=3) ). CQFD. Sauf erreurs.
Dernière édition par nmo le Lun 23 Avr 2012, 19:22, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 23 Avr 2012, 18:53 Lun 23 Avr 2012, 18:53 | |
| Je propose: Problème 104:Déterminez tous les entiers n tel que  est un entier. Bonne chance. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
