Préparations aux olympiades de tronc commun (2010-2011)

Boubou-maths t'es de fès? parce que moi aussi je passerai les olympiades demain à oumou Aymane

oué je suis de Fes , on passe cet apem BONNE CHANCE A TOI

plizz jai trouvé dans une question c'est quoi le nombre qui suit directement 3.25 dans N et Q

c'est quand les résultats des olympiades ?

Salut voici un nouveau problème :
Problème 91

Soit le polynôme tel que a un nombre réel.
Calculez

si x différant de 1 f(x)=x^n+ a((1-x^n)/1-x))
si x=1 f(x)=1+na
maintenant si 1-a=1 ----> a=0 f(1-a)=f(1)=1
et si 1-a différant de 0 f(1-a)=(1-a)^n+a(1-(1-a)^n)/a=1
conclusion f(1-a)=1

ali-mes a écrit:

Posons on a
AC²+BD²=(AI+IC)²+(BI+ID)²
AC²+BD²=AI²+2.AI.IC+IC²+BI²+2.BI.ID.ID²
AC²+BD²=(AI²+BI²)+(IC²+ID²)+2.AI.IC+2.BI.ID
AC²+BD²=AB²+CD²+2.AI.IC+2.BI.ID

d'autre part on a (AB+CD)²=AB²+CD²+2.AB.CD
et on a (AB)ll(CD) donc d'après Thalès on a
.................et j'ai stoppé ici je crois que ça un rapport avec le produit scalaire [je crois]

Hamouda a écrit:

euh.. je pense qu'il fallait dire que les cotés parallèles du trapèze sont (AB) et (DC)

Posons O l'intersection de (AC) et (BD)

je vais procédais par équivalence:

(AB+DC)²=AC²+BD²
AB² + DC² + 2*AB.DC= (AO + OC)² + ( BO+OD)²
AB² + DC² + 2*AB.DC= (AO² + BO²) + (OC² + OD²) + 2*(AO.OC+BO.OD)

On fait pythagore dans AOB ET OCD et on remplace:

AB² + DC² + 2*AB.DC= AB² + DC²+ 2*(AO.OC+BO.OD)

AB.DC=AO.OC+BO.OD

Il est clair que:
produit scalaire(AB.DC)=AB.DC ( (AB) et (DC) parallèles)
produit scalaire(AO.OC)=AO.OC
produit scalaire(BO.OD)=BO.OD


euhh je n'ai aucune idée comment je peut écrire les vecteurs alors permettez moi d'écrire BO à la place de vecteur(BO) [Il n'y aura pas de mesures dans toute la partie restante, rien que des vecteurs jusqu'à la fin!)

Je continue la démo:

AB.DC=AO.OC+BO.OD
(AO+OB).(DO+OC)=AO.OC+BO.OD
AO.DO+AO.OC + OB.DO+OB.OC=AO.OC+OB.DO
AO.DO+OB.OC=0

(AO) et (DO) sont perpendiculaires, même chose pr (OB) et (OC)

AD.DO=0 et OB.OC=0

donc: AO.DO+OB.OC=0
càd: (AB+DC)²=AC²+BD²

Une courte solution :

Notons X un point de (AB) tel que (XD)//(AC) donc AXDC est un parallélogramme
D'où XA=CD et XD=AC
D'après Pitaghoras : XB²=XD²+DB²
(DC+AB)²=AC²+DB²

diablo902 a écrit:

ali-mes a écrit:

Posons on a
AC²+BD²=(AI+IC)²+(BI+ID)²
AC²+BD²=AI²+2.AI.IC+IC²+BI²+2.BI.ID.ID²
AC²+BD²=(AI²+BI²)+(IC²+ID²)+2.AI.IC+2.BI.ID
AC²+BD²=AB²+CD²+2.AI.IC+2.BI.ID

d'autre part on a (AB+CD)²=AB²+CD²+2.AB.CD
et on a (AB)ll(CD) donc d'après Thalès on a
.................et j'ai stoppé ici je crois que ça un rapport avec le produit scalaire [je crois]

Hamouda a écrit:

euh.. je pense qu'il fallait dire que les cotés parallèles du trapèze sont (AB) et (DC)

Posons O l'intersection de (AC) et (BD)

je vais procédais par équivalence:

(AB+DC)²=AC²+BD²
AB² + DC² + 2*AB.DC= (AO + OC)² + ( BO+OD)²
AB² + DC² + 2*AB.DC= (AO² + BO²) + (OC² + OD²) + 2*(AO.OC+BO.OD)

On fait pythagore dans AOB ET OCD et on remplace:

AB² + DC² + 2*AB.DC= AB² + DC²+ 2*(AO.OC+BO.OD)

AB.DC=AO.OC+BO.OD

Il est clair que:
produit scalaire(AB.DC)=AB.DC ( (AB) et (DC) parallèles)
produit scalaire(AO.OC)=AO.OC
produit scalaire(BO.OD)=BO.OD


euhh je n'ai aucune idée comment je peut écrire les vecteurs alors permettez moi d'écrire BO à la place de vecteur(BO) [Il n'y aura pas de mesures dans toute la partie restante, rien que des vecteurs jusqu'à la fin!)

Je continue la démo:

AB.DC=AO.OC+BO.OD
(AO+OB).(DO+OC)=AO.OC+BO.OD
AO.DO+AO.OC + OB.DO+OB.OC=AO.OC+OB.DO
AO.DO+OB.OC=0

(AO) et (DO) sont perpendiculaires, même chose pr (OB) et (OC)

AD.DO=0 et OB.OC=0

donc: AO.DO+OB.OC=0
càd: (AB+DC)²=AC²+BD²

Une courte solution :

Notons X un point de (AB) tel que (XD)//(AC) donc AXDC est un parallélogramme
D'où XA=CD et XD=AC
D'après Pitaghoras : XB²=XD²+DB²
(DC+AB)²=AC²+DB²

Je vous propose cette solution en utilisant le produit scalaire :
puisque (AB) et (DC) sont parralelles donc (AB+DC)²=( AB(v) + DC(v) )² = ( AC(v)+CB(v)+DB(v)+BC(v))²=(AC(v)-BD(v) )² = AC²+BD² ( AC(v) perpendiculaire sur BD(v)

slt les amis je croit que vaut reponse ne sont pas du niveau TC nn ? comme chebishev , etc ... cher pas trop moi

redouaneamraouza a écrit:

slt les amis je croit que vaut reponse ne sont pas du niveau TC nn ? comme chebishev , etc ... cher pas trop moi

...=??

exo 92 :
je viens d'avoir cet exo en olympiade

En absurde en pose a>1 b>2 c>3 ...g>10 1+2+3+...10=55 >50 imp

redouaneamraouza a écrit:

slt les amis je croit que vaut reponse ne sont pas du niveau TC nn ? comme chebishev , etc ... cher pas trop moi

Mais oui voyans c pas de notre niveau, dailleurs on te demande pas de surpasser ton niveau d'études en olymp, l'exercice est fat pour etre résolu de telle façon que l'élève utilise inteligemment ses ressources et nn pas autres choses

Exo 93:
Prouvez que est divisible par 19.

Problème 94:

on a l'inégalité est équivalente a : ab+ac+bc-2abc >1\4 , maintenant on pose : a=x+y , b=y+z , c=x+z ; on a x+y+z=1\2 , l'inégalité se transforme en : x²+y²+z²+2(xy+yz+xz)+2xyz > 1\4 , équivalant a : (x+y+z)²+2xyz >1\4 équivalent : xyz >0 ce qui est vrai .

Problème 95 : a,b,c >=0 . Prouver que :

Oty a écrit:

Problème 95 : a,b,c >=0 . Prouver que :

Solution au problème 95:
d'après Holder
[img]http://latex.codecogs.com/gif.latex?[\frac{1}{b(a+b)}+\frac{1}{c(b+c)}+\frac{1}{a(c+a)}](a+b+c)[(a+b)+(b+c)+(c+a)]&space;\ge&space;(1+1+1)^3 [/img]
d'où le résultat

Bonsoir , je ne vois pas ou est l'inégalité de Holder dans ton expression tu peux préciser ?

Pour le problème 96: on prend x=0 on a : |c| =< 1 , pour la 2) on prend x=1 puis x=-1 en sommant on obtient le résultat , 3) toujours avec x=1 et x=-1 en faisant la différence des deux inégalité on trouve |b|=<1 , et on a a²+b²+c²=(|a+b+c|)²-2b(a+c)-2bc =<1+2(|b|.|a+c|+|bc|) =<1+2(1+1)=5 ( car |x| >= x quelque soit x dans R)

Problème 97 : x,y>=0 tel que : 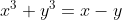. Montrer que : .

Oty a écrit:

Problème 97 : x,y>=0 tel 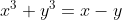que : . Montrer que : .

Je pense que quelque chose ne marche pas bien dans cet exercice.
En effet, si on considère x un paramètre, l'équation 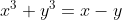, dont l'inconnue est y, admet une solution réelle .
(Tu peux utiliser la méthode de Cardan ou voir dans le lien suivant: [url]http://www.wolframalpha.com/input/?i=x-x^3%3Dy%2By^3 [/url]).
Et ainsi, l'inégalité à démontrer s'écrit .
Ce qui n'est pas valide, d'après Wolfram Alpha: [url]http://www.wolframalpha.com/input/?i=4%28\frac{%28-27x^3%2B\sqrt{%2827x-27x^3%29^2%2B108}%2B27x%29^{\frac{1}{3}}}{3.2^{\frac{1}{3}}}%2B\frac{2^{\frac{1}{3}}}{%28-27x^3%2B\sqrt{%2827x-27x^3%29^2%2B108}%2B27x%29^{\frac{1}{3}}}%29^2%2Bx^2%3C1 [/url].
Veille à vérifier l'énoncé.

je ne vois pas vraiment pourquoi tout c'est calcule ? il n'y a pas d'erreur dans l'énoncé et l'inégalité ce démontre simplement , pas besoin de cardan .