| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
+46Norax Mehdi-el redouaneamraouza Misterayyoub diablo902 *youness* Loliiiita kaj mima ilyasaitazzi l'intellectuelle az360 konica darkpseudo Mehdi.O maths_lady mathadores amigo-6 K-maths youpi alumenne.b achraf_djy boubou math yumi M.Marjani Nayssi Meded louis yasserito master Othmaann houssa ayoubmath nmo Dijkschneier mizmaz belkhayaty Azerty1995 tarask Hamouda anas-az_137 matheux-xman Ahmed Taha (bis) maths-au-feminin A446 supista ali-mes 50 participants |
|
| Auteur | Message |
|---|
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 30 Déc 2010, 21:20 Jeu 30 Déc 2010, 21:20 | |
| Salut,
Alors solution du probleme 59,
Soient a et b deux réels;
a>b
a-b>0
Il existe un entier naturel q tel que :
q(a-b)>1
qa-qb>1
D'ou l'existence d'un entier relatif p tel que :
qb<p<qa
Soit b<p/q<a
Ainsi entre deux reels se trouve necessairement un rationnel.
Voilà
Sinon je vais poster un exercice (déjà proposé par Azerty dans un autre sujet) en plus de celui proposé par Matheux-xman:
Probleme 61:
Montrez que pour tout n appartrenant a IN*/{1;2}
n^(n+1)>(n+1)^n
http://latex.codecogs.com/gif.latex?n^{n+1}%3E(n+1)^n | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 02 Jan 2011, 20:00 Dim 02 Jan 2011, 20:00 | |
| Pour le probleme 61 je vous donne quelques indices:
1) Montrer que n>(1+1/n)^n pour out n appartenant IN*/{1;2}
(Indication: Raisonnez par réccurence)
2) En déduire le résultat
Bonne chance | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 06 Jan 2011, 13:16 Jeu 06 Jan 2011, 13:16 | |
| pr exo 1 l'inégalité est juste quelque soit a,b,c voila une demonstration:
a/b+c + b/a+c + c/a+b = (a/b+c +1)+(b/a+c +1)+(c/a+b +1)-3=(a+b+c/b+c)+(a+b+c/a+c)+(a+b+c/a+b)-3=(a+b+c)((1/b+c) +(1/a+c)+(1/a+b))-3= 1/2((b+c)+(a+c)+(a+b))((1/b+c)+(1/a+c)+(1/a+b)-3
on sait que (x+y+z)(1/x +1/y +1/z) >=9 alors
((a+b)+(b+c)+(a+c))(1/a+b + 1/b+c + 1/a+c)>=9 donc
1/2 ((a+b)+(b+c)+(a+c))(1/a+b + 1/b+c + 1/a+c) -3>= 9/2 -3 = 3/2
a/b+c + b/a+c + c/a+b>=3/2
| |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 13 Jan 2011, 18:45 Jeu 13 Jan 2011, 18:45 | |
| | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 13 Jan 2011, 18:58 Jeu 13 Jan 2011, 18:58 | |
| - Nayssi a écrit:
- Pour le probleme 61 je vous donne quelques indices:
1) Montrer que n>(1+1/n)^n pour out n appartenant IN*/{1;2}
(Indication: Raisonnez par réccurence)
2) En déduire le résultat
Bonne chance Salut J'arrive pas à resoudre, peux-tu poster ta réponse? | |
|
  | |
achraf_djy
Expert grade1

 Nombre de messages : 401 Nombre de messages : 401
Age : 33
Localisation : Rabat
Date d'inscription : 01/08/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 13 Jan 2011, 19:09 Jeu 13 Jan 2011, 19:09 | |
| - Nayssi a écrit:
- Pour le probleme 61 je vous donne quelques indices:
1) Montrer que n>(1+1/n)^n pour out n appartenant IN*/{1;2}
(Indication: Raisonnez par réccurence)
2) En déduire le résultat
Bonne chance Salam! le raisonnement par récurrence n'est pas au programme de tc, c'est au 1ère an du bac! | |
|
  | |
alumenne.b
Maître

 Nombre de messages : 73 Nombre de messages : 73
Age : 29
Localisation : Fes
Date d'inscription : 08/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 18 Jan 2011, 22:31 Mar 18 Jan 2011, 22:31 | |
| Sauf svp j'ai une petite intervention pour [b]problème 59:
(a²+b²)c=c(a+b)²-2abc
(b²+c²)a=a(b+c)²-2abc ====) c(a+b)²+a(b+c)²+b(a+c)²>=6abc
b(a²+c²)=b(a+c)²-2abc
ce pendant (a+b)²=a²+b² sauf si 2ab=0
et meme chose pour les autres | |
|
  | |
youpi
Débutant
 Nombre de messages : 10 Nombre de messages : 10
Age : 29
Date d'inscription : 11/01/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mer 19 Jan 2011, 20:20 Mer 19 Jan 2011, 20:20 | |
| voilà ma méthode pour exo 1: on a <=b<=c donc (1/a+c) <= (1/b+c) <= (1/a+b) d'àpres l'inégalité du réordonnement : (a/a+c) +(b/b+c) +(c/a+b) >= (a/a+c)+(b/a+b)+(c/b+c) et: (a/a+c) +(b/b+c) +(c/a+b)>= (c/a+c)+(b/b+c)+(a/a+b) la somme des deux inégalités donne : 2 ((a/a+c) +(b/b+c) +(c/a+b))>=(a/a+c)+ (c/a+c)+(b/a+b)+ (a/a+b)+ (c/b+c)+(b/b+c) donc 2 ((a/a+c) +(b/b+c) +(c/a+b))>=3 d ou (a/a+c) +(b/b+c) +(c/a+b) >= 3/2  | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mer 26 Jan 2011, 15:49 Mer 26 Jan 2011, 15:49 | |
| Solution Probleme 61:
Montrons que : n>(1+1/n)^n pour tout n appartenant à IN*/{1;2}
Initialisation : Pour n=3 , (1+1/3)^3=(4/3)^3=64/27<3 On a alors :
n>(1+1/n)^n pour n=3
Heredité : Supposons que n>(1+1/n)^n
soit : n(1+1/n)>(1+1/n)^n+1
n+1>(1+1/n)^n+1
De plus :
n+1>n
1/(n+1)<1/n
1<1+(1/(n+1))<1+(1/n)
[1+(1/(n+1)]^n+1<(1+1/n)^n+1
Soit [1+1/(n+1)]^n+1<(1+1/n)^n+1<n+1
En particulier : [1+1/(n+1)]^n+1<n+1
Par Conséquent, nous venons de montrer par récurrence que:
n>(1+1/n)^n
soit n>[(n+1)/n]^n
n> [(n+1)^n]/(n^n)
soit n*n^n>(n+1)^n
n^n+1>(n+1)^n QED
Je pose un autre problème pour relancer ce sujet :
Problème 62
Discuter suivant les valeurs des paramètres a et b et résoudre dans IR l’équation suivante :
x/a + a/x = x/b + b/x
| |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 27 Jan 2011, 20:56 Jeu 27 Jan 2011, 20:56 | |
|
Dernière édition par Azerty1995 le Ven 28 Jan 2011, 12:16, édité 1 fois | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 27 Jan 2011, 21:07 Jeu 27 Jan 2011, 21:07 | |
| Je suis entièrement d'accord avec toi jusqu'à l'equivalence :
(b-a)(x²-ab)=0 OK
Mais là voila ce que ca devrait donner :
<=> b=a OU x²-ab=0
Donc là tu dois trouver les solutions dans chaque cas
A vous de jouer | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 27 Jan 2011, 21:20 Jeu 27 Jan 2011, 21:20 | |
| Salut
tu as raison ça devient
S={a,-a,Vab,-Vab}
J'attends ta confirmation | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 27 Jan 2011, 21:57 Jeu 27 Jan 2011, 21:57 | |
| Pas vraiment!!!
En fait pour a, b et x non nuls on distingue deux cas :
1) a-b=0 soit a=b
S={IR*} (x non nul)
2) x²-ab=0
Ainsi x=Vab ou x=-Vab
S={Vab ; -Vab}
Voilà
A toi de proposer un nouvel exo
| |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 28 Jan 2011, 12:31 Ven 28 Jan 2011, 12:31 | |
| Salut Problème 63Soit a, b et c des réels positifs tel que 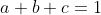 Montrez que : ^{2}+(b-1)^{2}+(c-1)^{2}\geq \frac{4}{3}) Bonne chance. | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 | |
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 | |
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 28 Jan 2011, 17:48 Ven 28 Jan 2011, 17:48 | |
| 3[(a-1)²+(b-1)²+(c-1)²]=(1²+1²+1²)[(a-1)²+(b-1)²+(c-1)²]
D'après Inegalité de C-S :
(1+1+1)[(a-1)²+(b-1)²+(c-1)²]>=[1(a-1)+1(b-1)+1(c-1)]²
Donc :
3[(a-1)²+(b-1)²+(c-1)²]>=(a-1+b-1+c-1)²=(a+b+c-3)²=(1-3)²=4 (a+b+c=1)
Ainsi :
3[(a-1)²+(b-1)²+(c-1)²]>=4
D'où: (a-1)²+(b-1)²+(c-1)²>=4/3
Problème 64 :
Résoudre dans IN :
xy+x+2y=20
Bonne Chance!!!
| |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 28 Jan 2011, 19:06 Ven 28 Jan 2011, 19:06 | |
| Salut
Solution du problème 64
xy+x+2y=20
x(y+1)+2y+2=22
x(y+1)+2(y+1)=22
(y+1)(x+2)=22
Donc:
y+1=1
x+2=22
===> y=0 et x= 20
ou
x+2=1
y+1=22
===> x=-1 n'appartient pas a IN
ou
y+1=2
x+2=11
===> y=1 et x =9
ou
y+1=11
x+2=2
====> y=10 et x =0
Donc
S={20,0);(9,1);(0,10)}
Problème 65
Soit (ABC) un triangle équilateral
M, N et K sont trois points appartenant respectivement à [AB] ,[BC] et [AC] tel que AM=BN=CK
Montrez que le triangle (MNK) est equilateral
Bonne chance.
| |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 28 Jan 2011, 20:25 Ven 28 Jan 2011, 20:25 | |
| Salut,  ABC équilateral et M, N et K sont trois points appartenant respectivement à [AB] ,[BC] et [AC] tel que AM=BN=CK=x (1) On a : AB=BC=AC=y Alors : MB=AB-AM=y-x CN=CB-BN=y-x AK=AC-CK=y-x Donc : MB=CN=AK (2) De plus, ABC étant équilatéral : angle(ABC)=angle(BCA)=angle(CAB)=60° Et comme M, N et K sont trois points appartenant respectivement à [AB] ,[BC] et [AC] Alors : angle(ABC)=angle(MBN) angle(BCA)=angle(NCK) angle(CAB)=angle(KAM) D'où angle(MBN)=angle(NCK)=angle(KAM) (3) De (1),(2) et (3) on peut déduire que : Les triangles CNK, BNM et AKM sont isométriques Par conséquent : KN=MN=KM D'où (MNK) un triangle équilatéral Problème 66Soit n un entier naturel non nul Montrer qu'il n'existe pas d'entier naturel p tel que n²+1=p² Bonne chance   | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 28 Jan 2011, 21:50 Ven 28 Jan 2011, 21:50 | |
| Salut
Solution du problème 66
Supposont que p est un entier naturel
On a
n²+1=p²
<=> n²-p²=-1
<=>(n-p)(n+p)=-1
n+p>0 car n et p sont de naturels
Donc n+p=1 d'ou n=1-p
n>0 <=> 1-p>0
<=> p<1
Le seul entier naturel strictement inferieur à 1 est 0
n²+1=0 absurde car n²+1>0
Donc il n'existe pas d'entier naturel p tel que n²+1=p²
| |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 28 Jan 2011, 22:26 Ven 28 Jan 2011, 22:26 | |
| Salut Problème 67Définir x et y de IN tel que : 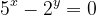 Bonne chance | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Sam 29 Jan 2011, 00:42 Sam 29 Jan 2011, 00:42 | |
| c pas qqch ayant relation au logarithme ou kkch? | |
|
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Sam 29 Jan 2011, 10:24 Sam 29 Jan 2011, 10:24 | |
| Solution du problème67: On a 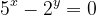 Donc 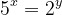 Or 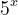 se termine toujours par 5, et 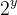 se termine par 2, 4, 8, 6. Donc le seul cas d'égalité c'est x=y=0. D'ou \}) | |
|
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Sam 29 Jan 2011, 10:34 Sam 29 Jan 2011, 10:34 | |
| Problème 68:Déterminer une équation du second degré admettant deux solutions 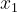 et 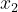 telsque ^2+(x_{1}x_{2}+2)^2=0) . | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Sam 29 Jan 2011, 12:45 Sam 29 Jan 2011, 12:45 | |
| Solution Probleme 68
Soit Le polynôme de second degré P(x)=ax²+bx+c ET x1 et x2 ses racines
On peut facilement démontrer que : x1*x2=c/a et x1+x2=(-b)/a
On a (x1²+x2²-5)²+(x1x2+2)²=0
Donc : (x1²+x2²-5)²=0 soit x1²+x2²-5=0 soit x1²+x2²=5
Or x1+x2=(-b)/a
Donc (x1+x2)²=b²/a² soit x1²+x2²+2x1x2=b²/a² soit x1²+x2²=b²/a² - 2ac/a² = (b²-2ac)/a²
Ainsi (b²-2ac)/a²=5 soit b²-2ac=5a² (1)
Et (x1x2+2)²=0 soit x1x2+2=0 soit x1x2=-2 Ainsi c/a=-2 d'où c=-2a
En remplaçant c par -2a en (1) on obtient :
b²-2a(-2a)=5a² soit b²+4a²=5a² soit b²=a² d'où b=a ou b=-a
Par conséquent on distingue deux cas :
a=b=-(c/2)
a=-b=-(c/2)
Par conséquent Les polynômes de la forme suivante vérifient la condition:
P(x)=ax²+ax-2a
OU
P(x)=ax²-ax-2a
Dernière édition par Nayssi le Dim 30 Jan 2011, 17:13, édité 2 fois | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
