| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
+46Norax Mehdi-el redouaneamraouza Misterayyoub diablo902 *youness* Loliiiita kaj mima ilyasaitazzi l'intellectuelle az360 konica darkpseudo Mehdi.O maths_lady mathadores amigo-6 K-maths youpi alumenne.b achraf_djy boubou math yumi M.Marjani Nayssi Meded louis yasserito master Othmaann houssa ayoubmath nmo Dijkschneier mizmaz belkhayaty Azerty1995 tarask Hamouda anas-az_137 matheux-xman Ahmed Taha (bis) maths-au-feminin A446 supista ali-mes 50 participants |
|
| Auteur | Message |
|---|
ayoubmath
Maître

 Nombre de messages : 216 Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 13:12 Lun 20 Déc 2010, 13:12 | |
| tu es sur que x^8+x+1=(x^2+x+1)(x^4-x^5+x^3-x^2+1) | |
|
  | |
maths-au-feminin
Maître
 Nombre de messages : 70 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 13:15 Lun 20 Déc 2010, 13:15 | |
| (x^2+x+1)(x^4-x^5+x^3-x^2+1) = -x^7+x^5+x^4+x+1 | |
|
  | |
ayoubmath
Maître

 Nombre de messages : 216 Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 13:20 Lun 20 Déc 2010, 13:20 | |
| pour probleme 31
on pose A=l'aire de tringle ABC et AB=a et AC=c
ona 2A=aCF=bBE donc BE=CF car a=b
maintenant on suppose que BE=CF
on a 2A=aCF=bBE donc a=b | |
|
  | |
ayoubmath
Maître

 Nombre de messages : 216 Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 13:31 Lun 20 Déc 2010, 13:31 | |
| problème 32 :
soit a,b,c les cotés d'un triangle tel que a+b+c=1
montrer que a²+b²+c²+4abc<1/2
bonne chance | |
|
  | |
maths-au-feminin
Maître
 Nombre de messages : 70 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 13:42 Lun 20 Déc 2010, 13:42 | |
| | |
|
  | |
maths-au-feminin
Maître
 Nombre de messages : 70 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 13:44 Lun 20 Déc 2010, 13:44 | |
| voilà un nouveau exo
Problème 33:
déterminer tous les entiers n tel que n²+8n-20 soit un carré parfait.
| |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 13:51 Lun 20 Déc 2010, 13:51 | |
| n²+8n-20 est un carré parfait 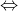 n²+8n-20=p² ( 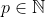 ) n²+8n-20=p² n²+8n+16-16-20=p² (n+4)²-36=p² (n+4)²-p²=36 (n+4-p)(n+4+p)=36 déterminons les diviseurs de 36 on a  et puisque  alors:      et puisque  les solutions acceptés sont n=6 ou n=2 CQFD
Dernière édition par ali-mes le Lun 20 Déc 2010, 16:34, édité 2 fois | |
|
  | |
matheux-xman
Féru

 Nombre de messages : 34 Nombre de messages : 34
Age : 28
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 14:23 Lun 20 Déc 2010, 14:23 | |
| - ayoubmath a écrit:
- tu es sur que x^8+x+1=(x^2+x+1)(x^4-x^5+x^3-x^2+1)
erreur de frappe, c'est x^8+x+1=(x^2+x+1)(x^ 6-x^5+x^3-x^2+1) | |
|
  | |
matheux-xman
Féru

 Nombre de messages : 34 Nombre de messages : 34
Age : 28
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 15:52 Lun 20 Déc 2010, 15:52 | |
| Problème 34 :
soient p et q deux entiers strictement positifs tel que : p/q = 1-1/2+1/3-.....-1/1318+1/1319.
montrer que p est un multiple de 1979. | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 17:00 Lun 20 Déc 2010, 17:00 | |
|
Dernière édition par ali-mes le Lun 20 Déc 2010, 17:48, édité 1 fois | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 17:27 Lun 20 Déc 2010, 17:27 | |
| Je vous propose ces deux exos: Problème 35:soient a et b deux réels strictement positifs. M.Q:  puis chercher le cas d'égalité. Problème 36:Existe-t-il un polynôme P(x) dont les coefficients sont entiers et vérifiant P(1)=4 et P(4)=9 ? | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 17:31 Lun 20 Déc 2010, 17:31 | |
| - ali-mes a écrit:
- Ma méthode pour problème 34:
-\left%20(%201+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{659}%20\right%20))
Je penses que tu as commis une faute de calcul, 3 au lieu de 1. Et à la fin de la démonstration, qui te garantit que x est un entier? | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 17:47 Lun 20 Déc 2010, 17:47 | |
| NN il fallait écrire -2(1/2 +1/4 .......... C ÉDITE maintenant  et pour x ====== j'ai pas fait attention | |
|
  | |
matheux-xman
Féru

 Nombre de messages : 34 Nombre de messages : 34
Age : 28
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 17:56 Lun 20 Déc 2010, 17:56 | |
| - ali-mes a écrit:
- Je vous propose ces deux exos:
Problème 35:
soient a et b deux réels strictement positifs.
M.Q: 
puis chercher le cas d'égalité.
Problème 36:
Existe-t-il un polynôme P(x) dont les coefficients sont entiers et vérifiant P(1)=4 et P(4)=9 ? Pour le probleme 35 : on a a^2+1>=2a et b^2+1>=2b donc (a^2+1)/b + (b^2+1)/a >= 2(a/b + b/a) >= 4 probleme 36 : si les coefficients sont des entiers naturelle : on a deg(P)<2 car sinon P(4)>=16 on pose P(x)=nx+m par P(4)=9 et P(1)=4 on aura un systeme à deux equations qui n'admet pas de solution dans IN ! | |
|
  | |
matheux-xman
Féru

 Nombre de messages : 34 Nombre de messages : 34
Age : 28
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 17:57 Lun 20 Déc 2010, 17:57 | |
| Pour la solution de ali-mes ... félicitation  ... c'est la bonne réponse  | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 18:01 Lun 20 Déc 2010, 18:01 | |
| | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 18:04 Lun 20 Déc 2010, 18:04 | |
| | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 18:06 Lun 20 Déc 2010, 18:06 | |
| | |
|
  | |
matheux-xman
Féru

 Nombre de messages : 34 Nombre de messages : 34
Age : 28
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 18:19 Lun 20 Déc 2010, 18:19 | |
| est ce que les coefficients sont des entiers naturelles ???? | |
|
  | |
matheux-xman
Féru

 Nombre de messages : 34 Nombre de messages : 34
Age : 28
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 18:27 Lun 20 Déc 2010, 18:27 | |
| - ali-mes a écrit:
- matheux-xman a écrit:
- Pour la solution de ali-mes ... félicitation
 ... c'est la bonne réponse ... c'est la bonne réponse 
mais il y a un problème : Qui nous garantit que x est un entier naturel ?   ah non, surement "x" n'est pas un entier naturel, c'est un nombre rationel de Q qui peux s'ecrire sous la forme p'/q', q' = 660*661*....*1319 1979p'q = pq' ... 1979^q' = 1 (car 1979 premier) donc 1979 devise p! j'ai dit que c'est juste car j'ai cru que vous avez pensé de la sorte  | |
|
  | |
matheux-xman
Féru

 Nombre de messages : 34 Nombre de messages : 34
Age : 28
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 19:50 Lun 20 Déc 2010, 19:50 | |
| problème 37 :Soit A la somme des chiffres du nombre  et B la somme des chiffres de A, Trouver la somme des chiffres du B | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 20 Déc 2010, 20:40 Lun 20 Déc 2010, 20:40 | |
| - matheux-xman a écrit:
Probleme 36 :
si les coefficients sont des entiers naturelle : on a deg(P)<2 car sinon P(4)>=16
on pose P(x)=nx+m
par P(4)=9 et P(1)=4 on aura un systeme à deux equations qui n'admet pas de solution dans IN ! Il n'est pas précisé que les coefficients sont des entiers naturelles (seulement des entiers). Ta solution n'est donc pas complète ... Dommage. Il y'a un petit résultat à connaitre: Si P est un polynôme à coefficients entiers alors (a-b)/(P(a)-P(b)). | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 12:45 Mar 21 Déc 2010, 12:45 | |
| Pour problème 37 je vais présenter un indice important et je posterai ma réponse ultérieurement.
Quand on fait la somme des chiffre d'un nombre, le reste de la division par 9 ne change pas. | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 13:01 Mar 21 Déc 2010, 13:01 | |
| Bon voilà la réponse pour le problème que matheux-xman a proposé. (Je l'ai trouvé en feuilletant les pages d'Internet) je crois que cet exo n'est pas convenable pour un niveau 2nde-TCS puisqu'il y a des modulos. voilà le lien: http://math.univ-lyon1.fr/~germoni/irem/7/4445.html Bah, en tous cas, voilà deux nouveaux exos pour ne pas retarder le jeu: Problème 38:soit a, b, c 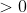 tel que abc=1 M.Q: \left%20(%20b-1+\frac{1}{c}%20\right%20)\left%20(%20c-1+\frac{1}{a}%20\right%20)\leq%201) Problème 39: Problème 39:Soit ABCD un quadrilatère convexe. Notons P le périmètre de ABCD. M.Q: ) | |
|
  | |
maths-au-feminin
Maître
 Nombre de messages : 70 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 14:19 Mar 21 Déc 2010, 14:19 | |
| pour problème 38 ____ aucune idée
et pour problème 39 ________ application directe de l'inégalité triangulaire | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
