| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
+46Norax Mehdi-el redouaneamraouza Misterayyoub diablo902 *youness* Loliiiita kaj mima ilyasaitazzi l'intellectuelle az360 konica darkpseudo Mehdi.O maths_lady mathadores amigo-6 K-maths youpi alumenne.b achraf_djy boubou math yumi M.Marjani Nayssi Meded louis yasserito master Othmaann houssa ayoubmath nmo Dijkschneier mizmaz belkhayaty Azerty1995 tarask Hamouda anas-az_137 matheux-xman Ahmed Taha (bis) maths-au-feminin A446 supista ali-mes 50 participants |
|
| Auteur | Message |
|---|
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 18:24 Mar 21 Déc 2010, 18:24 | |
| Solution au problème 38 :
Le changement de variable cyclique a|-> x/y étant fait, ce qui est possible compte tenu de la condition abc=1, l'inégalité devient : (x+y-z)(x+z-y)(y+z-x) <= xyz, ce qui n'est autre que l'inégalité de Schur (après développement). | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 19:33 Mar 21 Déc 2010, 19:33 | |
| Bonsoir !
Si ma mémoire est bonne , le problème 38 est un ancien IMO qui a été déjà posté ici mais la solution était différente que celle de Dijkschneier . | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 20:03 Mar 21 Déc 2010, 20:03 | |
| Oui tarask.
C'est en effet un ancien IMO et la solution que j'ai proposée est quand même bien connue. | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 20:13 Mar 21 Déc 2010, 20:13 | |
| | |
|
  | |
ayoubmath
Maître

 Nombre de messages : 216 Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 20:22 Mar 21 Déc 2010, 20:22 | |
| | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 20:30 Mar 21 Déc 2010, 20:30 | |
| - ayoubmath a écrit:
q pose son problème D'accord ! soient a,b et c trois réels strictement positifs tels que http://latex.codecogs.com/gif.latex?a+b+c=1 montrer que http://latex.codecogs.com/gif.latex?\150dpi%20a^{a}.b^{b}.c^{c}+%20a^{b}.b^{c}.c^{a}+a^{c}.b^{a}.c^{b}\preceq%201 Bonne chance  | |
|
  | |
ayoubmath
Maître

 Nombre de messages : 216 Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 20:48 Mar 21 Déc 2010, 20:48 | |
| voici ton p problème 40 :soient a,b et c trois réels strictement positifs tels que 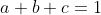 montrer que  | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 20:52 Mar 21 Déc 2010, 20:52 | |
| | |
|
  | |
ayoubmath
Maître

 Nombre de messages : 216 Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 20:59 Mar 21 Déc 2010, 20:59 | |
| comment b E R+* (réel) et on dit a^b !
| |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 21:04 Mar 21 Déc 2010, 21:04 | |
| - ayoubmath a écrit:
comment b E R+* (réel) et on dit a^b ! Oui . réel^réel  c'est clair non ? J'ai choisi ce problème que je trouve très joli , pour parler d'une inégalité qui est rarement utilisée , mais qu'il faut absolument connaître  | |
|
  | |
ayoubmath
Maître

 Nombre de messages : 216 Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 21:11 Mar 21 Déc 2010, 21:11 | |
| donc il faut que a,b,c E Q
je nai jamais conu réel^réel | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 21:18 Mar 21 Déc 2010, 21:18 | |
| - ayoubmath a écrit:
- donc il faut que a,b,c E Q
je nai jamais conu réel^réel Non , libère toi de ce que tu as étudié dans les premières leçons d'analyse (fonction racine n ième  ) Je ne comprend pourtant pas pourquoi tu ne l'accepte pas ce a^b  | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 21:36 Mar 21 Déc 2010, 21:36 | |
| salam : (By Am-Gm)
a²+b²+c²/a+b+c >= (a^a.b^b.c^c )^1/a+b+c ==> a²+b²+c²>=a^a.b^b.c^c
de meme pr prouver
ab+bc+ac>= a^b.b^c.c^a
et ac+ba+cb>a^c.b^a.^b
en sommant les 3 inégos
a^a.b^b.c^c+a^b.b^c.c^a +a^c.b^a.^b <= (a+b+c)²=1 | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 21:41 Mar 21 Déc 2010, 21:41 | |
| - master a écrit:
- salam : (By Am-Gm)
a²+b²+c²/a+b+c >= (a^a.b^b.c^c )^1/a+b+c ==> a²+b²+c²>=a^a.b^b.c^c
de meme pr prouver
ab+bc+ac>= a^b.b^c.c^a
et ac+ba+cb>a^c.b^a.^b
en sommant les 3 inégos
a^a.b^b.c^c+a^b.b^c.c^a +a^c.b^a.^b <= (a+b+c)²=1 Parfait ! C'est bien ça l'idée Weighted AM-GM | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 21:42 Mar 21 Déc 2010, 21:42 | |
| j'ai pas bien compris pouvez vous un peu detailler tarask svp!!? | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 21:45 Mar 21 Déc 2010, 21:45 | |
| Bonsoir yasserito :
Jette un coup d'oeil ici http://en.wikipedia.org/wiki/Inequality_of_arithmetic_and_geometric_means et si ça te pose encore problème, je suis prêt à l'expliquer . | |
|
  | |
ayoubmath
Maître

 Nombre de messages : 216 Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 21:48 Mar 21 Déc 2010, 21:48 | |
| svp tarask est ce que tu peux expliquer bien comment réel^réel
par exemple 2^pi =!! | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 21:50 Mar 21 Déc 2010, 21:50 | |
| En attente que klk1 poste un nouveau exo. | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 21:55 Mar 21 Déc 2010, 21:55 | |
| - ayoubmath a écrit:
- svp tarask est ce que tu peux expliquer bien comment réel^réel
par exemple 2^pi =!! T'as déjà fait l'exponentielle , le logarithme ? et bien je présume que oui ! à toi de voir maintenant  Sinon , on peut parler en mp pour ne pas polluer le sujet  (je t'ai préparé quelque chose --> mp ) | |
|
  | |
ayoubmath
Maître

 Nombre de messages : 216 Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 22:07 Mar 21 Déc 2010, 22:07 | |
| si vous voulez je propose un problème simple problème 41:soit  montrer que  pour tout n E N*-(1)
Dernière édition par ayoubmath le Mar 21 Déc 2010, 22:15, édité 1 fois | |
|
  | |
maths-au-feminin
Maître
 Nombre de messages : 70 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 22:13 Mar 21 Déc 2010, 22:13 | |
| | |
|
  | |
ayoubmath
Maître

 Nombre de messages : 216 Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 22:18 Mar 21 Déc 2010, 22:18 | |
| premierment on ne peux pas poser n=1 car S_n commence de 2 vers n
mais j'ai ajouté ce condition | |
|
  | |
maths-au-feminin
Maître
 Nombre de messages : 70 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
 | |
  | |
ayoubmath
Maître

 Nombre de messages : 216 Nombre de messages : 216
Age : 31
Date d'inscription : 07/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 21 Déc 2010, 22:51 Mar 21 Déc 2010, 22:51 | |
|
oui je sais
mais qui ta dit que ce pro a besoin de récurrence
la solution nécessite des règles simple
| |
|
  | |
maths-au-feminin
Maître
 Nombre de messages : 70 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
 | |
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
