Préparations aux olympiades de tronc commun (2010-2011)

Problème 41:
Démontrer que 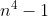est divisible par 5 si est seulement si n n'est pas un multiple de 5

Et pas besoin d'utiliser les MODULOS

d'accord
on a S_n>1 et on a n²-n<n² ===> 1/n²<1/n(n-1)=1/n-1 -1/n
===>1/2²<1-1/2 et 1/3²<1/2-1/3 .......1/n²<1/n-1 -1/n

===> S_n<2-1/n<2 ===> 1<S_n<2
on conclure

maths-au-feminin a écrit:

Problème 41:
Démontrer que est divisible par 5 si est seulement si n est un multiple de 5

n'est pas divisible par 5 si n est un multiple de 5

Je pense que le problème 41 doit avoir comme ennoncé :
Démontrer que 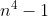est divisible par 5 si est seulement si n n'est pas un multiple de 5.
c'est une application directe du théoréme de fermat

oui t'as raison matheux-xman !!!!!!
c à toi de poster ta réponse (SANS UTILISER LA THÉORÈME DE FERMAT)

pour l'énoncé =----= C EDITE

Ma réponse pour le problème de maths-au-feminin

On a
et on a n n'est pas un multiple de 5 donc n=5k+1 ou n=5k+2 ou n=5k+3 ou n=5k+4 avec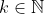

puis on fait les cas et on trouve que dans tous les cas 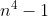est un multiple de 5.

voilà ces deux nouveaux exos (les deux son tirés de l'olympiade régionale de Tanger-Tétouan 2007):

Problème 42:
ABCD est un parallélogramme. M est un point de (AB)
N point d'intersection de (AD) et (MC).
prouve que

Problème 43:
(C) est un cercle de centre o.
A et B sont deux points différents et qui n'appartiennent pas à (C).
quand il est possible, expliquez la façon de dessiner deux points M et N de (C) tel que

Solution au problème 43 :
Soit h la translation de vecteur AB et k la translation de vecteur BA.
Pour construire les deux points M et N, on construit d'abord le cercle (C') image du cercle (C) par la translation h. Ces deux cercles se coupent alors en deux points : soit N l'un d'eux. Soit alors M l'image de N par la translation k. M appartient nécessairement à (C) car (C) est l'image de (C') par la translation de vecteur k. Nous avons nos deux points.

Fascinante ta méthode et pour problème 42 ?

M un point quelquonque de (AB)?

s'il appartient à [AB]: AB/AM > 1

ali-mes a écrit:

voilà ces deux nouveaux exos (les deux son tirés de l'olympiade régionale de Tanger-Tétouan 2007):

Problème 42:
ABCD est un parallélogramme. M est un point de (AB)
N point d'intersection de (AD) et (MC).
prouve que

j'ai trouvé que
ma démostration :
on a AB/AM=DC/AM=ND/AN
si M appartien à [AB] A et B non incluent , et pa théorème de thalés on trouve le resultat

très facile
voici ma démonstration

on a AD/AN=MC/MN=MB/MN
donc AB/AM+AD/AN=1-MB/MN+MB/MN=1 car AB=AM+MB

je veux bien partager avec vous cette problème

problème 43:
soit un droit (Δ) et A et B deux points fixe qui se trouvent dans la même coté de (Δ)

.......................B

.................................................................A

________________________________________ (Δ)


ou se trouve un point c E (Δ) dont la distance (AC+CB) est minimum

ayoubmath a écrit:

donc AB/AM+AD/AN=1-MB/MN+MB/MN

Comment ?????

pour matheux-xman
par thales on a normalement AN/ND=NM/NC ===> (ND-AD)/ND=(NC-MC)/NC
===> 1-AD/ND=1-MC/NC===>AD/ND=MC/NC

trace le figure pour bien comprendre

voilà ma méthode pour problème 41:












d'où

Ma réponse pour l'exo de ayoubmath:
Soit A' l'image de A par la symétrie de l'axe (D). donc n'importe qu'elle soit C de (D) on a CA=CA'. Et pour que CA+CB soit minimale, C et A et B doivent être allignés donc:

Problème 44:
Trouver a et b pour que le polynôme soit divisible par

voilà un nouveau exo de géométrie délicieux a résoudre

Problème 45:
Soit EBC un triangle. A et D sont deux points de [EB]-{E;B} et [EC]-{E;C} respectivement. supposons que (AD) coupe (BC) à F. et soit I et J et K les milieux respectives de [EF] et [BD] et [AC]. Démontre que I et J et K sont alignés.

ali-mes a écrit:

Problème 44:
Trouver a et b pour que le polynôme soit divisible par

x⁴+ax+b = (x+1)²(x²-2x+3) + (a-4)x+(b-3)
donc pour que soit divisible par
il faut que a=4 et b=3 ... sauf erreur

maths-au-feminin a écrit:

voilà un nouveau exo de géométrie délicieux a résoudre

Problème 45:
Soit EBC un triangle. A et D sont deux points de [EB]-{E;B} et [AC]-{A;C} respectivement. supposons que (AD) coupe (BC) à F.

est ce que F est confondu avec C ???

il ya un erreur dans ton pro ali-mes

problème 46:
soit

montrer que

Ma réponse poeur Problème 45:

Considérons B' la projection de B sur (EC) en parallèle avec (AD).
Dans le triangle EBB' on a (AD)ll(BB') donc:

Dans le triangle CDF on a (BB')ll(DF) donc:

Posons donc et donc



d'où
de (2) on conclut que
Et posons donc
d'où
de (3) on conclut que:

d'où

d'où
ننسب المستوى الى المعلم

Donc on a et et
on a


donc
et on a
donc
et on a



donc
On a I est le milieu de [EF] donc
et on a J est le milieu de [BD] donc
et on a K est le milieu de [AC] donc
d'où et
d'où
Et puisque alors I, J et K sont alignés.

SANS AUCUNE FAUTE D'INATTENTION DE MA PART.

ayoubmath a écrit:

il ya un erreur dans ton pro ali-mes

problème 46:
soit

montrer que

Quoi ?