Préparations aux olympiades de tronc commun (2010-2011)

avec plaisir
je vais proposer ces deux exos:

Problème 29:
trouves toutes les polynômes P(x) tel que (x-16)P(2x)=16(x-1)P(x)

Problème 30: (problème déjà proposé dans le forum mais pas encore résolu)
la somme de quatre nombres est 270 .
لو اضفنا 4 الى الاول و طرحنا 4 من التاني و ضعفنا التالت و اخدنا نصف الرابع لحصلنا على اربعة اعداد متساوية
اوجد الاعداد الاربعة

ali-mes a écrit:

SALAM
Moi aussi j'a pas trouvé la réponse pour le problème abdelkrim-amine
et pour l'exercice de maths-au-feminin il est simple {mini-EF }
voilà ma méthode:
on a f(x) est une polynôme et donc alors f(x) s'écrit sous la forme
d'où




donc

d'où

conclusion:

méthode excellente et bien organisée

c koi EF ?????????

EF = équation fonctionnelle = une équation dont les inconnues sont des fonctions

salam pour pb 28

une petite remarque: il suffit d'écrire x = 2y+1 , avec y = (x-1)/2

f(x) = f [2(x-1)/2 +1] =[(x-1)/2]² + 1/2.[(x-1)/2] + 3

= (x-1)²/4 + (x-1)/4 +3

= x²/4 - x/4 +3

______________________________________________________________

ma réponse pour problème 30
soient x et y et z et t ces nombres
on a (E): x+y+z+t=270
et x+4=y-4=2z=t/2

y-4=x+4 donc y=x+8
2z=x+4 donc z=(x+4)/2
t/2 =x+4 donc t=2x+8
en remplaçant dans E on trouve
que x=56
d'autre part on a (E'):y+z+t=214
2z=y-4 donc z=(y-4)/2
t/2=y-4 donc t=2y-8
en remplaçant dans E' on trouve
y=64
d'autre part on a (E"):z+t=150
et on a 2z=t/2 donc t=4z
d'où z=30
z+t=150 donc t=120
S={x=56/y=64/z=30/t=120} sans aucune faute de ma part

maths-au-feminin a écrit:

ma réponse pour problème 30
soient x et y et z et t ces nombres
on a (E): x+y+z+t=270
et x+4=y-4=2z=t/2

y-4=x+4 donc y=x+8
2z=x+4 donc z=(x+4)/2
t/2 =x+4 donc t=2x+8
en remplaçant dans E on trouve
que x=56
d'autre part on a (E'):y+z+t=214
2z=y-4 donc z=(y-4)/2
t/2=y-4 donc t=2y-8
en remplaçant dans E' on trouve
y=64
d'autre part on a (E"):z+t=150
et on a 2z=t/2 donc t=4z
d'où z=30
z+t=150 donc t=120
S={x=56/y=64/z=30/t=120} sans aucune faute de ma part

JUSTE et pour problème 29 ???

pour problème 30
il suffit de résoudre la système suivant :
* a+b+c+d=270
* a+4=b-4=2c=d/2

ali-mes a écrit:

maths-au-feminin a écrit:

ma réponse pour problème 30
soient x et y et z et t ces nombres
on a (E): x+y+z+t=270
et x+4=y-4=2z=t/2

y-4=x+4 donc y=x+8
2z=x+4 donc z=(x+4)/2
t/2 =x+4 donc t=2x+8
en remplaçant dans E on trouve
que x=56
d'autre part on a (E'):y+z+t=214
2z=y-4 donc z=(y-4)/2
t/2=y-4 donc t=2y-8
en remplaçant dans E' on trouve
y=64
d'autre part on a (E"):z+t=150
et on a 2z=t/2 donc t=4z
d'où z=30
z+t=150 donc t=120
S={x=56/y=64/z=30/t=120} sans aucune faute de ma part

JUSTE et pour problème 29 ???

pas encore

pour pro 29
est ce que la degré de P(x) na pas donné

Problème 29 :


q(x) vérifie :
donc : q(4)=0 et q( 8 )=0


P(x)=a(x-2)(x-4)( x - 8 )(x-16)

ayoubmath a écrit:

pour pro 29
est ce que la degré de P(x) na pas donné

on peut vérifier que le degré de P(x) est 4 puisque :
si deg(P)=n alors n vérifie 2^n = 16 donc n = 4

matheux-xman a écrit:

Problème 29 :


q(x) vérifie :
donc : q(4)=0 et q( 8 )=0


P(x)=a(x-2)(x-4)( x - 8 )(x-16)

juste c a twa de poster un nouveau problème

Je pense qu'il y a encore un problème non résolu, c'est celui de "abdelkrim-amine"
à savoir :
problème 27:
factoriser A et B:
A=x^8+x+1
B=x^10+x^5+1

remarque : si qls xER x^8+x+1#0

on ne peux pas factoriser A (je crois)

voilà un exo délicieux à résoudre de géométrie


PROBLÈME 31:
soit ABCD un parallélogramme. considérons les points A' B' C' et D' tel que A' مماثلة A par rapport à B et B' مماثلة par rapport à C et C' مماثلة C par rapport à D et D' مماثلة par rapport à A.
quelle est la nature du quadrilatère A'B'C'D' ?

ayoubmath a écrit:

remarque : si qls xER x^8+x+1#0

on ne peux pas factoriser A

Non, ce n'est pas vrai, on peux montrer que tout polynome dans IR peut être factroriser sous forme de produit des polynome de 1er et 2eme degré.

matheux-xman tu peux nou présenter ta méthode pour l'exo de factorisation

maths-au-feminin a écrit:

voilà un exo délicieux à résoudre de géométrie


PROBLÈME 31:
soit ABCD un parallélogramme. considérons les points A' B' C' et D' tel que A' مماثلة A par rapport à B et B' مماثلة par rapport à C et C' مماثلة C par rapport à D et D' مماثلة par rapport à A.
quelle est la nature du quadrilatère A'B'C'D' ?

un parallélogramme.
CQFD

maths-au-feminin a écrit:

voilà un exo délicieux à résoudre de géométrie


PROBLÈME 31:
soit ABCD un parallélogramme. considérons les points A' B' C' et D' tel que A' مماثلة A par rapport à B et B' مماثلة par rapport à C et C' مماثلة C par rapport à D et D' مماثلة par rapport à A.
quelle est la nature du quadrilatère A'B'C'D' ?

On vérifie que les deux triangles AD'A' et C'CB' متقيساًن donc A'D'=C'B'
idem on montre que C'D' = A'B'
donc A'B'C'D' est un parallélogramme

en attente que matheux-xman poste son factorisation

pour probleme 30
on justifier facilement que les triangles A'BB' et D'C'D est (متقايسة) aussi pour CC'B' et D'AA'
donc A'B'C'D' aussi est un parallélogramme

je suis toujours tard

ayoubmath a écrit:

pour probleme 30

on justifier facilement que les triangles A'BB' et D'C'D est (متقايسة) aussi pour CC'B' et D'AA'
donc A'B'C'D' aussi est un parallélogramme

la mm méthode que matheux-xman a présenté

pose ton problème ali-mes

ali-mes a écrit:

matheux-xman tu peux nou présenter ta méthode pour l'exo de factorisation

je n'est pas la solution complète
j'ai déviser le polynome x^8+x+1 sur x^2+x+1 j'ai trouvé que :
x^8+x+1=(x^2+x+1)(x^4-x^5+x^3-x^2+1)

B est aussi dévisible par x^2+x+1
B=(x^2+x+1)(x^8-x^7+x^5-x^4+x^3-x+1)

ayoubmath a écrit:

pose ton problème ali-mes

Avec plaisir.


Problème 31:
soient BE et CF deux hauteurs dans un triangle ABC.
M.Q: AB=AC 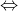AB+BE=AC+CF