Préparations aux olympiades de tronc commun (2010-2011)

ali-mes a écrit:

Ma réponse poeur Problème 45:

Considérons B' la projection de B sur (EC) en parallèle avec (AD).
Dans le triangle EBB' on a (AD)ll(BB') donc:

Dans le triangle CDF on a (BB')ll(DF) donc:

Posons donc et donc



d'où
de (2) on conclut que
Et posons donc
d'où
de (3) on conclut que:

d'où

d'où
ننسب المستوى الى المعلم

Donc on a et et
on a


donc
et on a
donc
et on a



donc
On a I est le milieu de [EF] donc
et on a J est le milieu de [BD] donc
et on a K est le milieu de [AC] donc
d'où et
d'où
Et puisque alors I, J et K sont alignés.

SANS AUCUNE FAUTE INATTENTION DE MA PART.

excellent
la mm methode qu'on a fait en classe (projection+thales+repere) mais on a choisi un autre repere .
pour ta demo j'ai seulement lu les grandes lignes ca parrait correcte

Problème 46:
Soient x et y deux réels strictement positifs tel que x+y=8.
M.Q:

Problème 47:
On considère un trapèze ABCD tel que (AB)ll(CD) et AB=84 et CD=25. On suppose qu'il existe un cercle inscrit dans ce trapèze. Quel est le périmètre de ce trapèze ?

Salut
Solution du probleme 46



On a

On sait que d'ou (1)

D'autre part on a

On remplace x+y par sa valeur (2)

On a aussi (3)

On fait la somme de (1) 2) (3) et on a le résultat

EXCELLENT

pour prob. 46 mm méthode k azerty1995 a fait mais pour l'autre exo de géométrie je l'ai pas encore résolu BON pour ne pas retarder le jeu voilà un nouveau exo

Problème 48:

Tjrs pas de réponses !!!

Voici la solution du problème 47:
https://mathsmaroc.jeun.fr/t15631-l-olympiade-de-settat-deuxieme-etape?highlight=settat
Bonne découverte.

ma réponse pour problème 47 est la mm que celle présentée dans le lien que louis a proposé.
est-ce-quelqu'un a pu résoudre l'exo que maths-au-feminin a présenter ?

personne n'a pu trouver la solution ???

en attente k klk1 pose sa réponse pour l'exo que j'ai propsé !!! je vous propse ces exos qui sont faciles un peu mais délicieux à résoudre:

Problème 49:
résoudre dans 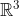le système:



Problème 50:
Résoudre dans : [img]http://latex.codecogs.com/gif.latex?\begin{matrix}%202\left%20[%202x-1%20\right%20]-1=5%20&%20&%20\\%202\left%20[%202x-1%20\right%20]-1=0%20&%20&%20\\%20\left%20[%20\frac{2x-3}{3}%20\right%20]=\frac{x-1}{3}&%20&%20\\%202\left%20[%20\frac{3x-1}{2}%20\right%20]\leq%201%20&%20&%20\end{matrix}[/img]




Problème 51:
f est une fonction numérique tel que: [img]http://latex.codecogs.com/gif.latex?\left\{\begin{matrix}%20f(x)=0%20\left%20\right%20&%20\forall%20x\in%20]-\infty;0]%20&%20\\%20f(x)=2x^2-x%20&%20\forall%20x\in%20[0;+\infty[%20&%20\end{matrix}\right[/img]



démontre que f(x) n'est pas un polynôme.

Ma réponse pour Problème49:



le système est équivalent à:

d'où

Puis, on résous le système et on trouve que x=1 et y=2
donc z=11-2-6=3
conclusion: S={1;2;3}

Dans le cas d'un système compliqué , on peut utiliser le Pivot de Gauss http://fr.wikiversity.org/wiki/Syst%C3%A8me_d%27%C3%A9quations_lin%C3%A9aires/Pivot_de_Gauss

P.S: clin d'oeil à Monsieur Lhassane qui nous a informés sur cette méthode dans un sujet

Ma réponse pour problème 50:

1)-
2[2x-1]-1=5
2[2x-1]=6
[2x-1]=3


d'où
donc S=[2;5/2[
2)-
2[2x-1]-1=0
[2x-1]=1/2
ce qui est absurde (car la partie entière d'un réel est toujours entière)
donc


3)-

On sait que la partie entière d'un réel est toujours entière. Alors posons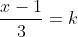
avec

donc x=3k+1
donc l'équation devient: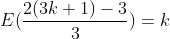
d'où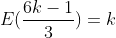
d'où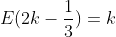
d'où (car )
d'où 2k+(-1)=k donc k=1
alors donc x=4
conclusion: S={4}


4)-
l'inéquation est équivalente à

d'où
donc
conclusion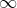: S=]-;1[

Ma réponse pour le dernier problème:

Montrons d'abord que f(x)[f(x)-(2x²-x)]=0
si donc f(x)=0
d'où f(x)[f(x)-(2x²-x)]=0.[0-(2x²-x)]=0
si donc f(x)=2x²-x d'où
f(x)[f(x)-(2x²-x)]=(2x²-x)(2x²-x-2x² x)=(2x²-x).0=0
d'où f(x)[f(x)-(2x²-x)]=0
[f(x)]²-f(x)(2x²-x)=0
[f(x)]²=f(x)(2x²-x)
Supposons que f(x) est une polynôme donc:
d'où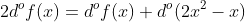
d'où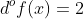
donc f(x) s'écrit sous la forme f(x)=ax²+bx+c avec
on a f(0)=0 et f(-1)=0 et f(-2)=0 f(1)=0

donc



la solution de système est (1/2;1/2)
Et puisque (1/2;1/2) ne satisfait pas l'équation 2a-b=0 alors il n'existe aucun
triplet (a;b;c) dans qui satisfait le système.
donc on peut pas écrire f(x) sous la forme f(x)=ax²+bx+c
coclusion: f(x) n'est pas un polynôme.

CQFD

En attente de vos critiques et que quelqu'un poste la réponse pour problème 48.

les réponses que ali-mes a proposé sont toutes complètes et justes.
bah !! pour ne pas retarder le jeu je vous propse ces 2 exos :


Problème 51:
démontre que la somme de 7 puissances consécutifs de 4 est divisible par 5461.

Problème 52:
x et y et z trois réels strictement positifs tel que xyz(x+y+z)=1
démontre que

t'es sur que c 4 puissances (je crois que c'est 7) !!!

Ma réponse pour problème 52:
on a (x+y)(y+z)=xy+xz+y²+yz=y(x+y+z)+xz
donc
d'où le résultat voulu.

oui tu as raison c 7 puissances consécutifs c édité maintenant

ma réponse pour problème 51:
Soient et les puissances voulus ()
on a
et avec l'aide du calculatrice on trouve que
d'où le résultat voulu

Je vous propose ces 2 exos:

Problème 53:
P(x) est un polynôme tel que
calcule P(11) et P(1) et P(-1)

Problème 54:
considérons ces 2 polynômes P(x) et Q(x) tel que avec n£IN
démontre que Q(x) divise P(x)

matheux-xman a écrit:

ali-mes a écrit:

Problème 44:
Trouver a et b pour que le polynôme soit divisible par

x⁴+ax+b = (x+1)²(x²-2x+3) + (a-4)x+(b-3)
donc pour que soit divisible par
il faut que a=4 et b=3 ... sauf erreur

J'ai pas compris ta méthode !!!!§§§
En tous cas voilà ma méthode:
(x+1)² divise x^4+ax+b signifie qu'il existe un polynôme P(x) à coefficients réels tel que
x^4+ax+b=(x+1)²P(x)
ce qui implique que deg(P(x))=2
donc P(x) s'écrit sous la forme P(x)=mx²+nx+p (avec m £ IR*)
donc x^4+ax+b=(x²+2x+1)(mx²+nx+p )
d'où x^4+ax+b=mx^4+(n+2m)x^3+(p+2n+m)x²+(2p+n)x+p

ce qui implique que

donc a=4 et b=3

Ma réponse pour problème 53:


d'autre part on a:



donc