| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
+46Norax Mehdi-el redouaneamraouza Misterayyoub diablo902 *youness* Loliiiita kaj mima ilyasaitazzi l'intellectuelle az360 konica darkpseudo Mehdi.O maths_lady mathadores amigo-6 K-maths youpi alumenne.b achraf_djy boubou math yumi M.Marjani Nayssi Meded louis yasserito master Othmaann houssa ayoubmath nmo Dijkschneier mizmaz belkhayaty Azerty1995 tarask Hamouda anas-az_137 matheux-xman Ahmed Taha (bis) maths-au-feminin A446 supista ali-mes 50 participants |
|
| Auteur | Message |
|---|
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 26 Déc 2010, 18:57 Dim 26 Déc 2010, 18:57 | |
| salam ! Puisque personne n'a posé une réponse pour problème 46 (moi aussi je l'ai pas résolu) C a vous de nous enrichir avec la réponse .....  AMICALEMENT | |
|
  | |
matheux-xman
Féru

 Nombre de messages : 34 Nombre de messages : 34
Age : 28
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 27 Déc 2010, 01:39 Lun 27 Déc 2010, 01:39 | |
| Réponse pour le problème 54 : on sait que pour tout entier non nul k :  dévisible par  , donc  dévisible par  donc P(x) dévisible par Q(x) | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 27 Déc 2010, 10:39 Lun 27 Déc 2010, 10:39 | |
| | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 27 Déc 2010, 10:59 Lun 27 Déc 2010, 10:59 | |
| Problème 55:Déterminer tous les entiers naturel a et b pour lesquels le nombre  est rationnel | |
|
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 27 Déc 2010, 16:56 Lun 27 Déc 2010, 16:56 | |
| | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 27 Déc 2010, 18:59 Lun 27 Déc 2010, 18:59 | |
| C'est à quelqu'un d'autre de proposer un nouveau exo  AMICALEMENT | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 27 Déc 2010, 19:20 Lun 27 Déc 2010, 19:20 | |
| Salut Pronlème 56 :Montrez que:  Problème 57 Problème 57Soit a et b deux réels tel que : 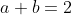 Montrez que :.  Bonne chance. | |
|
  | |
Meded
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 29
Date d'inscription : 27/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 27 Déc 2010, 19:54 Lun 27 Déc 2010, 19:54 | |
| sqrt : racine
(sqrt a - sqrt b)^2>= 0 ( si a et b sont positis)
a - 2 sqrt ab + b >=0
Or, a+b = 2
2>= 2 sqrt ab
1>= sqrt ab
puisque une racine est positive alors
0=<sqrt ab=<1
donc 0=<ab=<1
(a+b)^2 = a^2+ 2ab + b^2 = 4
on pose : 0=<2ab=<2
donc a^2+b^2>2
on élève au carré
(a^2+b^2)^2>=4
a^4 + 2a^2.b^2 + b^4>= 4
or, 0<=2.a^2.b^2<=2
On en déduit que a^4+b^4>=2
Dernière édition par Meded le Lun 27 Déc 2010, 20:29, édité 3 fois | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 27 Déc 2010, 20:02 Lun 27 Déc 2010, 20:02 | |
| - Meded a écrit:
- Pour le problème 57:
sqrt : racine
(sqrt a - sqrt b)^2>= 0
a - 2 sqrt ab + b >=0
Or, a+b = 2
2>= 2 sqrt ab
1>= sqrt ab
puisque une racine est positive alors
0=<sqrt ab=<1
donc 0=<ab=<1
(a+b)^2 = a^2+ 2ab + b^2 = 4
on pose : 0=<2ab=<2
donc a^2+b^2>2
on élève au carré
(a^2+b^2)^2>=4
a^4 + 2a^2.b^2 + b^4>= 4
or, 0<=2.a^2.b^2<=2
On en déduit que a^4+b^4>=2
Salut C' est faux on ne peut pas dire que  sauf si a et b sont positifsce n'est pas le cas essaye autrement  Bonne chance | |
|
  | |
Meded
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 29
Date d'inscription : 27/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Lun 27 Déc 2010, 20:32 Lun 27 Déc 2010, 20:32 | |
| En effet , je croyais qu'ils étaient positifs. | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 28 Déc 2010, 03:02 Mar 28 Déc 2010, 03:02 | |
| Solution Probleme 57 :
pour tout réel a et b.
On peut distinguer quatre cas possibles.
1) |a|<1 et |b|<1
-1<a<1 et -1<b<1
Soit -2<a+b<2
Or justement a+b=2
a ET b n'appartiennent donc pas à l'intervalle ]-1;1[
2) |a|>=1 et |b|<=1
soit : -|b|>=-1 et |a|>=1
En multipliant ces deux inégalités
-|ab|<= -1 (-|b| etant négatif)
|ab|>=1
3) |a|<=1 et |b|>=1
soit : 0>=-|a|>=-1 et |b|>=1
En multipliant ces deux inégalités
-|ab|<= -1
|ab|>=1
4) |a|>=1 et |b|>=1
Immédiatement on aura :
|ab|>=1
Comme a et b ont des rôles symetriques
Alors : Pour tout a de IR et b de IR/]-1;1[
|ab| >= 1
(rac(ab)²)>= 1 ( |x| = (rac(x)²)
(rac(ab)²)²>=1
(ab)²>=1 ( (rac(x))²= x pour x réel positif (carré toujours positif))
2(ab)²>=2 résultat (1)
On a : pour tout réel a et b :
(a²-b²)²>=0
a^4+b^4-2a²b²>=0
a^4+b^4>=2(ab)² résultat (2)
Des résultats (1) et (2) on déduit que : a^4+b^4>=2(ab)²>=2
Ainsi particulièrement :
a^4+b^4>=2 QED
En attendant vos remarques,
Dernière édition par Nayssi le Mar 28 Déc 2010, 19:33, édité 1 fois | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 28 Déc 2010, 13:10 Mar 28 Déc 2010, 13:10 | |
| - Nayssi a écrit:
- Solution Probleme 57 :
pour tout réel a et b
Si -1<a<1 et -1<b<1 alors -2<a+b<2 et donc a+b#2
Or a+b = 2
Ainsi (a,b) n'appartiennent pas à l'intervalle ]-1;1[ soit |a|>=1 et |b|>=1
D'ou |ab| >= 1
(rac(ab)²)>= 1 ( |x| = (rac(x)²)
(rac(ab)²)²>=1
(ab)²>=1 ( (rac(x))²= x pour x réel positif (carré toujours positif))
2(ab)²>=2 résultat (1)
On a : pour tout réel a et b :
(a²-b²)²>=0
a^4+b^4-2a²b²>=0
a^4+b^4>=2(ab)² résultat (2)
Des résultats (1) et (2) on déduit que : a^4+b^4>=2(ab)²>=2
Ainsi particulièrement :
a^4+b^4>=2 QED
En attendant vos remarques,
Salut  Je pense que c'est juste, mais je crois que tu as oublié un cas : si a appertient a l'intervalle ]-1,1[ et b n' y appartient pas ? Je ne suis pas sure, et ej veux bien savoir ce qu' en pense les autres Bonne chance | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 28 Déc 2010, 15:59 Mar 28 Déc 2010, 15:59 | |
| Ah oui c'est vrai ,
Dans le cas : a appartient à l'intervalle ]-1;1[ , b non.
On a : |a|<=1 et |b|>=1
soit : 0>=-|a|>=-1 et |b|>=1
En multipliant ces deux inégalités
-|ab|<= -1
|ab|>=1
On revient à notre inégalité.
| |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 28 Déc 2010, 16:58 Mar 28 Déc 2010, 16:58 | |
| - Nayssi a écrit:
- Ah oui c'est vrai ,
Dans le cas : a appartient à l'intervalle ]-1;1[ , b non. Tu auras un tone de cas, méme - selon la methode que t'as suivi - tu ne peut rien faire si a=<0 et b>=0... Il faut chercher donc une autre methode. Solution 57:- Spoiler:
(a+b)^4=(a²+2ab+b²)(a²+2ab+b²)=a^4+b^4+4ab((a+b)²-2ab)+6(ab)²
<=> a^4+b^4=16-4ab(4-2ab)+6(ab)²=16-16ab+14(ab)²
Donc il vous suffit de MQ: 14(ab)²-16ab+16>=2 <=> q(ab)²-(8/7)ab+1>=0 tel que q=1 [J'ai dévisé par 14]
Delta= 64/49 - 4<0. Et car q=1>0 qu'on aura forcément (ab)²-(8/7)ab+1>=0.
| |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 28 Déc 2010, 19:26 Mar 28 Déc 2010, 19:26 | |
|  Salut M.Marjani, en fait je pose des inégalités faisant intervenir |a| , |b| ET 1 Je vais traiter donc les 4 SEULS cas possibles: 1) |a|<1 et |b|<1 C'est le cas où a+b<2 a ET b n'appartiennent donc pas à l'intervalle ]-1;1[ 2) |a|>=1 et |b|<=1 soit : -|b|>=-1 et |a|>=1 En multipliant ces deux inégalités -|ab|<= -1 (-|b| etant négatif) |ab|>=1 On revient à notre inégalité. 3) |a|<=1 et |b|>=1 soit : -|a|>=-1 et |b|>=1 En multipliant ces deux inégalités -|ab|<= -1 (-|a| étant négatif) |ab|>=1 On revient à notre inégalité. 4) |a|>=1 et |b|>=1 Immédiatement on aura : |ab|>=1 On revient à notre inégalité. Je pense que c'est juste. J'attends vos remarques PS:J'ai édité ma démonstration ci-dessus | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 28 Déc 2010, 20:00 Mar 28 Déc 2010, 20:00 | |
| - Nayssi a écrit:
 Salut Salut
M.Marjani, en fait je pose des inégalités faisant intervenir |a| , |b| ET 1
Je vais traiter donc les 4 SEULS cas possibles:
1) |a|<1 et |b|<1
C'est le cas où a+b<2
a ET b n'appartiennent donc pas à l'intervalle ]-1;1[
2) |a|>=1 et |b|<=1
soit : -|b|>=-1 et |a|>=1
En multipliant ces deux inégalités
-|ab|<= -1 (-|b| etant négatif)
|ab|>=1
On revient à notre inégalité.
3) |a|<=1 et |b|>=1
soit : -|a|>=-1 et |b|>=1
En multipliant ces deux inégalités
-|ab|<= -1 (-|a| étant négatif)
|ab|>=1
On revient à notre inégalité.
4) |a|>=1 et |b|>=1
Immédiatement on aura :
|ab|>=1
On revient à notre inégalité.
Je pense que c'est juste. J'attends vos remarques
PS:J'ai édité ma démonstration ci-dessus
Bien joué, belle méthode. Il vous reste l'autre problème. Bonne chance | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 28 Déc 2010, 20:37 Mar 28 Déc 2010, 20:37 | |
| Solution problème 56
Dans la somme : 1/101+1/102+1/103+...+1/199 , Il y a 99 son termes.
On sait que pour tout a et b de IR : Si a<=b alors 1/a>=1/b
Donc
1/200<=1/101
1/200<=1/102
1/200<=1/103
. .
. .
. .
. .
1/200<=1/199
1/200+1/200+1/200+...+1/200 <= 1/101+1/102+1/103+...+1/199
99 fois
99 x (1/200) + 1/200 <= 1/101+1/102+1/103+...+1/199+1/200
(1/200) (99+1) <= 1/101+1/102+1/103+...+1/199+1/200
100 x (1/200) <= 1/101+1/102+1/103+...+1/199+1/200
1/2 <= 1/101+1/102+1/103+...+1/199+1/200
Je pense que c'est juste me je n'en suis pas sûr
J'attends vos critiques
| |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 28 Déc 2010, 20:43 Mar 28 Déc 2010, 20:43 | |
| - Nayssi a écrit:
- Solution problème 56
Dans la somme : 1/101+1/102+1/103+...+1/199 , Il y a 99 son termes.
On sait que pour tout a et b de IR : Si a<=b alors 1/a>=1/b
Donc
1/200<=1/101
1/200<=1/102
1/200<=1/103
. .
. .
. .
. .
1/200<=1/199
1/200+1/200+1/200+...+1/200 <= 1/101+1/102+1/103+...+1/199
99 fois
99 x (1/200) + 1/200 <= 1/101+1/102+1/103+...+1/199+1/200
(1/200) (99+1) <= 1/101+1/102+1/103+...+1/199+1/200
100 x (1/200) <= 1/101+1/102+1/103+...+1/199+1/200
1/2 <= 1/101+1/102+1/103+...+1/199+1/200
Je pense que c'est juste me je n'en suis pas sûr
J'attends vos critiques
C'est juste, à toi de postr un problème. | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 28 Déc 2010, 21:36 Mar 28 Déc 2010, 21:36 | |
| OK  | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 28 Déc 2010, 22:16 Mar 28 Déc 2010, 22:16 | |
| Probleme 58 a,b,c trois réels positifs. Montrer que : (a²+b²)c+(b²+c²)a+(c²+a²)b>=6abc Probleme 59 Montrer qu'entre deux réels se trouve un rationnel Bon courage   
Dernière édition par Nayssi le Mer 29 Déc 2010, 00:36, édité 1 fois | |
|
  | |
yumi
Maître

 Nombre de messages : 156 Nombre de messages : 156
Age : 30
Localisation : {Univers des éventualités}U/{My Land}
Date d'inscription : 08/11/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mer 29 Déc 2010, 00:09 Mer 29 Déc 2010, 00:09 | |
| ma réponse du problème58:
est ce que a,b,c ,sont des réels positifs??
si c le cas alors:
on a :(a²+b²)c>=2abc
(b²+c²)a>=2abc
(c²+a²)b>=2abc
en sommant les trois ,on trouve le résultat...
sinon s'ils ne sont que des réels ma réponse sera fausse je pense,donc j'essaierai autrement! | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mer 29 Déc 2010, 00:17 Mer 29 Déc 2010, 00:17 | |
| | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mer 29 Déc 2010, 00:33 Mer 29 Déc 2010, 00:33 | |
| Salut - yumi a écrit:
- ma réponse du problème58:
est ce que a,b,c ,sont des réels positifs??
si c le cas alors:
on a :(a²+b²)c>=2abc
(b²+c²)a>=2abc
(c²+a²)b>=2abc
en sommant les trois ,on trouve le résultat...
sinon s'ils ne sont que des réels ma réponse sera fausse je pense,donc j'essaierai autrement! Effectivement, je me suis trompé....Les trois réels doivent être positifs. Ta démonstration est juste....bien joué!!!  - Citation :
- Rouge , la notion d'Archimédien
P.S:(et un irrationnel ) Je ne connais pas cette notion. Mais en tout cas on peut le faire autrement...(Niveau Tronc commun)    | |
|
  | |
matheux-xman
Féru

 Nombre de messages : 34 Nombre de messages : 34
Age : 28
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 30 Déc 2010, 15:56 Jeu 30 Déc 2010, 15:56 | |
| je me permet de vous poser le 60ème Problème : Montrer que l'inégalité : (\sum_{i=1}^{n}b_i^{2})}{(\sum_{i=1}^{n}a_ib_i)^2}\leq&space;\frac{(m+M)^2}{4mM}) est valable pour tous réels 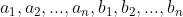 vérifiant 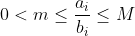
Dernière édition par matheux-xman le Jeu 30 Déc 2010, 16:06, édité 1 fois | |
|
  | |
matheux-xman
Féru

 Nombre de messages : 34 Nombre de messages : 34
Age : 28
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 30 Déc 2010, 15:58 Jeu 30 Déc 2010, 15:58 | |
| Pour vous aider un peu, pensez à la méthode de démonstration de l'inégalité de CS  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
