Préparations aux olympiades de tronc commun (2010-2011)

oui c'est vrai ... le probleme de soupista me semble trés dûr, est ce que tu peut nous donner juste un indice

je vais vous donner un indice, car sinon ça ne va pas âtre amusant pour vous
remarquer que l’équation est équivalente à cette équation:
(4x-1)(4y-1)=4z^2+1
Dans une heure ou plus je vais poster la solution

time's over !! je poste la solution
J'ai fais de mon mieux pour détailler la solution, et la rendre le plus claire possible, c'est pour ça que ça parait un peu long.

On veux trouver toutes les solutions dans N*xN*xN* de l'equation: 4xy-x-y=z^2
cette équation est équivalente à :(4x-1)(4y-1)=4z^2+1(*) (simple calcule suffit pour montrer ça)
remarquer que pour x>0 et y>0 on a 4x-1>2 donc 4x-1 admet un nombre premier p (forcément impair) comme diviseur, l'équation (*) devient modulo p:
(2z)^2+1=0 (mod p) c'est à dire: (2z)^2=-1 (mod p)
d'après le petit théorème de fermat on a (2z)^{p-1}=1 (mod p) (1) mais si on pose r=(p-1)/2 on a :
(2z)^{p-1}=(2z)^{2r}=((2z)^2)^r=(-1)^r (mod p) (2)
de (1) et (2) on a : 1=(-1)^r (mod p) ce qui ne peut pas etre vrais que si 1=(-1)^r c'est à dire si r=(p-1)/2 est pair ainsi p=1 (mod 4)
on a ainsi montrer que tous les diviseurs premier de 4x-1 sont congrues à 1 modulo 4
si on décompose 4x-1 en produit de nombres premiers on a 4x-1=p_1p_2...p_n est pour tout i ona p_i=1 (mod 4)
Donc 4x-1=1 (mod 4) d'ou -1=1 (mod 4) contradiction !! donc ya pas de solution

Puisque personne n'a résolu cet exercice, j'ai toujours la main cette fois je vais poster un exercice de solution plus simple et astucieuse comme même

" On suppose que le polynome P(x)=x^4-2x^2+ax+b ,avec a et b sont des réels, admet quatre racines, q,r,s,t deux à deux différentes montrer que la valeur absolue de chaque racine de P est strictement inférieure au racine carré de 3"

jolie coup
pour la solus

ah je comprend la regle,
il faut resoudre un exo pour avoir la main
cool comme regle

ça fait une demi heure pour comprendre votre solution !!! je pense que c'est assez dûr pour un niveau Seconde - Tronc commun !!!! mais joli coup tout de même

sa c vrai, y a un new théorème avec polynomes+équations,
mais cela ne fait qu'enrichir nos connaissances et techniques
thx pour notre ami supista ^^

oui t'as raison, mais c'est un exercice tiré des Olympiades, et dans les olympiades on vous demande toujours d’être un peu "hors programme", bon l'autre exercice ne demande aucun théorème hors programme à part les relations de Viete entre les racines et les coefficients d'un polynome, cette relation bien qu'elle soit hors programme est indispensable aux olympiades même au niveau de tronc commun, quand j'étais participant aux olympiades au lycée j'ai pas fais un exercice car "JE NE SAVAIS PAS LES FORMULES DE VIETE", j'ai fais exprès de donner ce genre d'exercice, car je juge qu'ils contiennent des méthodes et des idées très importante.
Pour les formules de viete voilà un lien wikipedia qui explique très bien: http://fr.wikipedia.org/wiki/Relations_entre_coefficients_et_racines

formidable supista !!!!!
puisque personne n'a posté aucun problème je vais poster ces deux exos:
problème5:
a et b deux réels positifs tel que a²-b²=1
M.Q:
problème6:
soit n un entier naturel non-nul
M.Q: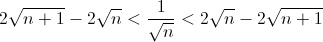
puis calcule
on note [z] le plus grand entier inférieur ou égal a z:

en fait j'ai déjà posté un autre

" On suppose que le polynome P(x)=x^4-2x^2+ax+b ,avec a et b sont des réels, admet quatre racines, q,r,s,t deux à deux différentes montrer que la valeur absolue de chaque racine de P est strictement inférieure au racine carré de 3"

pour les deux problemes que tu viens de poster, ils sont faciles ( sans vouloir te vixer )

supista a écrit:

en fait j'ai déjà posté un autre

" On suppose que le polynome P(x)=x^4-2x^2+ax+b ,avec a et b sont des réels, admet quatre racines, q,r,s,t deux à deux différentes montrer que la valeur absolue de chaque racine de P est strictement inférieure au racine carré de 3"

pour les deux problemes que tu viens de poster, ils sont faciles ( sans vouloir te vixer )

En fait supista , il y a d'autres resultats plus forts pour des polynômes s'écrivent sous la forme : (Grand terme de x est pondéré par le coefficient 1), Comme ses racines 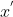(Que se soient complexes ou réels)sont toujours :

: l'indice 'i' débute à partir de zéro

ali-mes a écrit:

:

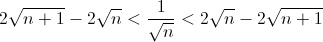
je pense que cette inégalité est fausse, puisque la partie droite est négative!

ali-mes a écrit:

formidable supista !!!!!
puisque personne n'a posté aucun problème je vais poster ces deux exos:
problème5:
a et b deux réels positifs tel que a²-b²=1
M.Q:
problème6:
soit n un entier naturel non-nul
M.Q: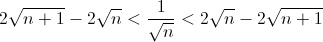
puis calcule
on note [z] le plus grand entier inférieur ou égal a z:

pr l'exo 6:

il y a une faute: sqrt(n) - sqrt(n+1) < 0 donc c impo que ça soit plus grand que 1/sqrt(n) qui est positif...

je pense que tu voulais plutot dire: 1/sqrt(n) < 2*sqrt(n) - 2*sqrt(n-1)

démo:

( sqrt(n+1) - sqrt(n) ) ^2 > 0
<==> n+1+n - 2*sqrt (n)*sqrt(n+1) >0
<==> 2*sqrt(n)*sqrt(n+1) -2n < 1
<==> 2*sqrt(n+1) - 2*sqrt(n) < 1/sqrt(n)

( sqrt(n-1) - sqrt(n) )^2 >0

(de la méme façon... on trouve: 1/sqrt(n) < 2sqrt(n) -2*sqrt(n-1)


pour la question 2 je ne vais pas faire avant d'étre sur de l'énoncé^^

@anas-az_137: ton résultat n'est pas plus fort , je le connais déjà et aussi sa démonstration, en fait le résultat de l'exercice que j'ai poser est très fort et on ne peux pas choisir un nombre plus petit que racine 3, c'est un exercice d'olympiade !!!!
bah essayez de résoudre ça, au lieu de s'amuser à résoudre des exercice faciles

supista a écrit:

@anas-az_137: ton résultat n'est pas plus fort , je le connais déjà et aussi sa démonstration, en fait le résultat de l'exercice que j'ai poser est très fort et on ne peux pas choisir un nombre plus petit que racine 3, c'est un exercice d'olympiade !!!!
bah essayez de résoudre ça, au lieu de s'amuser à résoudre des exercice faciles

en fait j'ai rien dit , j'ai seulment dit résultat plus fort au cas générale , ton exercice est réduit en une seule cas qui peut être traité comme le cas générale (enfin j'y pense , j'ai pas éssayé)....Merci pour ton conseil !

Bon après-midi supista .
Je suis très content de voir quelqu'un qui encourage les TC à préparer les olympiades , mais j'ai une toute petite remarque : les exercices que vous proposez sont un peu difficiles pour les TC , qui ne sont censés que connaître quelques simples formules en géométrie , inégalités.....
Mais en tout cas c'est une très bonne initiative de votre part , sauf que je suis sûr que quelques uns auront du mal à suivre

Salut
Solution du probleme 5

D'apres l'IAG on a:

1/(a+b)^n+1/(a-b)^n >=2V(1/[(a+b)(a-b)]^n
> =2V(1/(a²-b²)^n
>=2

Probleme 7

Definir a et b de IR tel que
3V(a-9)+5V(b-25)=(a+b)/2
Bonne chance

dsl supista j'é pas vu l probleme k tu as postéé !!! oops

wéé pou le 6eme probleme j'ai commis une faute de frappe !! dsl
et le probleme k tu as posté je l'ai trouvé dur puisque je ne maitrise pas bien les polynomes

@ anas-az_137 : si c'est le cas tu peux nous éclaircir avec une démonstration ?
@tarask :tas raison, et j'ai un peu exagérer peut etre, mais je pense que ça ne sert à rien de faire des choz qu'on sait déjà faire , pas vrai ?! en tant que ex-candidat aux olympiades, j'ai vu la préparation des autres pays, ils font des exercices plus difficiles et ils sont pourtant trop jeune, il faut que nous soyons nous les Marocains à la hauteur !!! pour l'autre exercice ,c'est pas difficile mais astucieux certes.

tarask a écrit:

Bon après-midi supista .
Je suis très content de voir quelqu'un qui encourage les TC à préparer les olympiades , mais j'ai une toute petite remarque : les exercices que vous proposez sont un peu difficiles pour les TC , qui ne sont censés que connaître quelques simples formules en géométrie , inégalités.....
Mais en tout cas c'est une très bonne initiative de votre part , sauf que je suis sûr que quelques uns auront du mal à suivre

je supporte le point de vue de tarask
mmssab hnaya fel jid3 nte9nu gha les choses initiales (les inégualités ou la géometrie ...... ) ra tante9nu haduk mezyann ama ra kayen f had l forum des rubriques décidés pour les bacheliers ou la superieurs ....

Si "makate9ench mezyane" les olympiades c'est pas pour vous

Azerty1995 a écrit:

Salut
Probleme 7

Definir a et b de IR tel que
3V(a-9)+5V(b-25)=(a+b)/2
Bonne chance

je ne comprend pas votre "V", est ce que tu peux réecrire ton énoncé

supista a écrit:

@ anas-az_137 : si c'est le cas tu peux nous éclaircir avec une démonstration ?
@tarask :tas raison, et j'ai un peu exagérer peut etre, mais je pense que ça ne sert à rien de faire des choz qu'on sait déjà faire , pas vrai ?! en tant que ex-candidat aux olympiades, j'ai vu la préparation des autres pays, ils font des exercices plus difficiles et ils sont pourtant trop jeune, il faut que nous soyons nous les Marocains à la hauteur !!! pour l'autre exercice ,c'est pas difficile mais astucieux certes.

Certes Monsieur !
Les autres pays s'entrainent à un échelle plus élevé que le notre , mais , eux , ils se préparent avec des coachs de haute renommée et ne sont ainsi pas très gênés par le programme , or , nous les marocains on fournit plus d'efforts pour se préparer seuls , ou bien entre élèves comme c'est le cas ici.
En tout cas , comme j'ai dit , c'est une très bonne initiative de votre part de faire monter un petit peu la difficulté des exercices .