| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
+46Norax Mehdi-el redouaneamraouza Misterayyoub diablo902 *youness* Loliiiita kaj mima ilyasaitazzi l'intellectuelle az360 konica darkpseudo Mehdi.O maths_lady mathadores amigo-6 K-maths youpi alumenne.b achraf_djy boubou math yumi M.Marjani Nayssi Meded louis yasserito master Othmaann houssa ayoubmath nmo Dijkschneier mizmaz belkhayaty Azerty1995 tarask Hamouda anas-az_137 matheux-xman Ahmed Taha (bis) maths-au-feminin A446 supista ali-mes 50 participants |
|
| Auteur | Message |
|---|
maths-au-feminin
Maître
 Nombre de messages : 70 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 17 Déc 2010, 13:04 Ven 17 Déc 2010, 13:04 | |
| MA RÉPONSE (FINALEMENT) posons 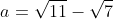 on peut écrire la polynôme P(x) s'écrit sous la forme 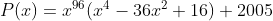 donc 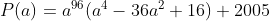 d'autre part on a 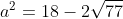 donc  d'où 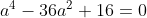 alors 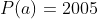 sans aucune faute de ma part   pour l'autre exo je l'ai pas encore résolu (mais je vais je l'espère  ) | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 17 Déc 2010, 13:18 Ven 17 Déc 2010, 13:18 | |
| Oui c'est ça, BRAVO  | |
|
  | |
maths-au-feminin
Maître
 Nombre de messages : 70 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 17 Déc 2010, 13:39 Ven 17 Déc 2010, 13:39 | |
| on sait que  est un corps commutatif donc on peut supposer que  parce que la relation  :(1) ne change pas en changeant les places de m et n et p si p=0 donc (1) s'écrit sous la forme m+n=0 donc m=n=0 si p=1 donc (1) s'écrit sous la forme m+n+1=mn d'où (m-1)(n-1)=2 donc m-1=2 et n-1=1 (car  ) donc m=3 et n=2 si 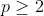 donc  car  et puisque  car 2mn-m-n=(m-1)(2n-1)-1 et  alors  conclusion: conclusion: S={(0,0,0);(1,2,3);(1,3,2);(2,1,3);(2,3,1);(3,1,2);(3,2,1)} avec aucune faute  est un corps commutatif résume tous ........ les propriétés de la somme et le produit dans 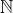 en attente de vos critiques mais pas maintenant car j'ai un examen de maths a 2h. C mon tour de poster un nouveau exo bye | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 17 Déc 2010, 18:45 Ven 17 Déc 2010, 18:45 | |
| - maths-au-feminin a écrit:
- on sait que
 est un corps commutatif donc on peut supposer que est un corps commutatif donc on peut supposer que  parce que la relation parce que la relation  :(1) :(1)
ne change pas en changeant les places de m et n et p
si p=0 donc (1) s'écrit sous la forme m+n=0 donc m=n=0
si p=1 donc (1) s'écrit sous la forme m+n+1=mn d'où (m-1)(n-1)=2 donc m-1=2 et n-1=1 (car  ) donc m=3 et n=2 ) donc m=3 et n=2
si 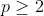 donc donc  car car 
et puisque  car 2mn-m-n=(m-1)(2n-1)-1 et car 2mn-m-n=(m-1)(2n-1)-1 et 
alors 
conclusion:
S={(0,0,0);(1,2,3);(1,3,2);(2,1,3);(2,3,1);(3,1,2);(3,2,1)}
avec aucune faute
 est un corps commutatif résume tous ........ les propriétés de la somme et le produit dans est un corps commutatif résume tous ........ les propriétés de la somme et le produit dans 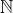
en attente de vos critiques mais pas maintenant car j'ai un examen de maths a 2h. C mon tour de poster un nouveau exo
bye Corps commutatif, pfiou... A 15 ans ! | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 17 Déc 2010, 19:08 Ven 17 Déc 2010, 19:08 | |
| oui mizmaz tu as raison, je crois qu'il fallait juste dire que en changeant les places de m et n et p la valeur de l'équation ne change pas(الجمع و الضرب في مجموعة الاعداد الصحيحة الطبيعية تجميعي و تبادلي ) . et je dis pas ce qu'elle a dit est faux mais ça ne figure pas dans notre programme (ni dans le programme de 1ere) en tous cas ce qu'elle a écrit est 100 pour 100 DESERVE A THUMB-UP bon pour ne pas retarder le jeu voilà un nouveau problème: problème 16:soient x, y, et z dans  + M.Q:  et déterminer le cas d'égalité | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 17 Déc 2010, 20:24 Ven 17 Déc 2010, 20:24 | |
| - maths-au-feminin a écrit:
- en attente de vos critiques
- maths-au-feminin a écrit:
- on sait que
 est un corps commutatif donc on peut supposer que est un corps commutatif donc on peut supposer que  (N,+,x) est un corps commutatif ?! Non.. Puisque c'est un corps commutatif, on peut mettre un ordre ?! Non.. Solution au problème 16 :L'inégalité est équivalente à :  Ce qui est une application de l'inégalité du réordonnement. Le cas d'égalité est atteint pour x=y=z. Et je n'ai pas de problème adapté à proposer. | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 17 Déc 2010, 20:41 Ven 17 Déc 2010, 20:41 | |
| Bonsoir tout le monde .
En fait , le problème 15 figure dans un ancien test de Tronc-commun de la région Tétouan-Tanger .
Je crois avoir déjà vu une réponse semblable à celle de maths-au-féminin.
| |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 17 Déc 2010, 20:46 Ven 17 Déc 2010, 20:46 | |
| c mon prof qui m'a proposé cet exo........ et je crois que tarask a raison
en-tt-cas les taupins n'hésitez pas à nous enrichir avec vos exos
AMICALEMENT | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 17 Déc 2010, 21:11 Ven 17 Déc 2010, 21:11 | |
| puisque personne n'a posté aucun problème voilà un nouveau exo: problème 17:a, b et c trois nombres réels strictement positifs tel que a+b+c=1 M.Q:  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 17 Déc 2010, 21:15 Ven 17 Déc 2010, 21:15 | |
| Solution au problème 17 :Selon CS : ^2}{2(x+y+z)}%20=%20\frac{x+y+z}{2}%20=%20\frac{1}{2}) Et je n'ai pas de problème à proposer. | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 17 Déc 2010, 21:20 Ven 17 Déc 2010, 21:20 | |
| - ali-mes a écrit:
- puisque personne n'a posté aucun problème voilà un nouveau exo:
problème 17:
a, b et c trois nombres réels strictement positifs tel que a+b+c=1
M.Q:  sans vouloir gâcher votre jeu : - Spoiler:
Application directe de Cauchy-Schwartz 
| |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 | |
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 17 Déc 2010, 21:35 Ven 17 Déc 2010, 21:35 | |
| tout vos réponses sont fascinantes et justes c à klk1 d'autre de poster un nouveau exo  | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 17 Déc 2010, 21:40 Ven 17 Déc 2010, 21:40 | |
| Je n'ai pas de problème de niveau Tronc-commun , mais je vous ai créé cet exercice un peu banal pour ne pas arrêter votre préparation:
Résoudre dans Z²: 2x+3y=xy
Bonne chance . | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 17 Déc 2010, 21:55 Ven 17 Déc 2010, 21:55 | |
| FACILE
2x+3y=xy
xy-2x-3y=0
xy-2x-3y+6=+6
(x-3)(y-2)=6
(x;y)£ Z² donc
x-3=1 et y-2=6 donc x=4 et y=8
ou
x-3=-1 et y-2=-6 donc x=2 et y=-4
ou
x-3=6 et y-2=1 donc x=9 et y=3
ou
x-3=-6 et y-2=-1 donc x=-3 y=1
ou
x-3=2 et y-2=3 donc x=5 et y=5
ou
x-3=-2 et y-2=-3 donc x=1 et y=-1
ou
x-3=3 et y-2=2 donc x=6 et y=4
ou
x-3=-3 et y-2=-2 donc x=0 et y=0
coclusion
S={(4;8 )(2;-4)(9;3)(-3;1)(5;5)(1;-1)(6;4)(0;0)}
| |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 17 Déc 2010, 22:03 Ven 17 Déc 2010, 22:03 | |
| | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 17 Déc 2010, 22:05 Ven 17 Déc 2010, 22:05 | |
| Facile oui !
J'ai seulement lu les grandes lignes , ça parait correct !
| |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 17 Déc 2010, 22:08 Ven 17 Déc 2010, 22:08 | |
| Salut
Problème 19
Definissez x,y et z tel que
Vx +V(y-1) +V (z-2)=1/2(x+y+z)
PS: J'ai pas encore trouvé la solution pour ce problème
Bonne chance | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 17 Déc 2010, 22:42 Ven 17 Déc 2010, 22:42 | |
| Si tu veux bien t'entrainer sur les inégalités , essaye de travailler ce fichier http://www.eleves.ens.fr/home/kortchem/olympiades/Problemes/inegalites/i2006.pdf .
Bonne chance ! | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 17 Déc 2010, 22:44 Ven 17 Déc 2010, 22:44 | |
| Solution au problème 19 :%20+%20((y-1)-2\sqrt{y-1}+1)%20+%20((z-2)-2\sqrt{z-2}+1)%20=%200%20\Leftrightarrow%20(\sqrt{x}-1)^2%20+%20(\sqrt{y-1}-1)^2%20+%20(\sqrt{z-2}+1)^2%20=%200%20\Leftrightarrow%20(x,y,z)=(1,2,3)) Et je n'ai pas de problème adapté à proposer. | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Sam 18 Déc 2010, 13:41 Sam 18 Déc 2010, 13:41 | |
| voila ces deux nouveaux exos: Problème20:x, y et z trois nombres réels positifs tel que xyz=1. déterminer la valeur de S tel que 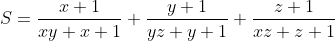 Problème21: Problème21:soit a, b, c, d et e des nombres réels. M.Q:  puis chercher le cas d'égalité | |
|
  | |
maths-au-feminin
Maître
 Nombre de messages : 70 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Sam 18 Déc 2010, 14:08 Sam 18 Déc 2010, 14:08 | |
| pour problème 21 : simple d'après IAG:  de la mm façon on démontre que    la somme donne le résultat voulut. CHERCHER LE CAS D'ÉGALITÉ: on a 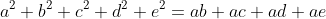 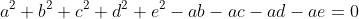  avec égalité seulement si  | |
|
  | |
maths-au-feminin
Maître
 Nombre de messages : 70 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
 | |
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Sam 18 Déc 2010, 14:30 Sam 18 Déc 2010, 14:30 | |
| EXCELLENT  | |
|
  | |
maths-au-feminin
Maître
 Nombre de messages : 70 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Sam 18 Déc 2010, 17:30 Sam 18 Déc 2010, 17:30 | |
| c mn tour à poster un nouveau problème: PROBLÈME 22:a, b, c £ Q. montrer que si ab+ac+bc=1 donc 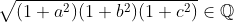 | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
