| | Préparations aux olympiades de tronc commun (2011-2012 ) |  |
|
+16hind nassri Didou-Touzani Ahmed Taha (bis) Norax konica ali-mes Mehdi.O Nayssi oiga aminox upsilon salimreda kaj mima Soukaina Amaadour rimetta diablo902 20 participants |
|
| Auteur | Message |
|---|
rimetta
Féru

 Nombre de messages : 57 Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
 |  Sujet: __ Sujet: __  Jeu 10 Nov 2011, 19:43 Jeu 10 Nov 2011, 19:43 | |
|
Dernière édition par rimetta le Jeu 10 Nov 2011, 19:59, édité 1 fois | |
|
  | |
oiga
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 28
Date d'inscription : 09/11/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 19:49 Jeu 10 Nov 2011, 19:49 | |
|
Dernière édition par oiga le Jeu 10 Nov 2011, 20:02, édité 1 fois | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 19:53 Jeu 10 Nov 2011, 19:53 | |
|
Dernière édition par diablo902 le Jeu 10 Nov 2011, 20:04, édité 1 fois | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 19:53 Jeu 10 Nov 2011, 19:53 | |
| rimetta c'est supprimé c faut | |
|
  | |
oiga
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 28
Date d'inscription : 09/11/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 19:55 Jeu 10 Nov 2011, 19:55 | |
| Mais je veux les deux
a et b
la somme
| |
|
  | |
oiga
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 28
Date d'inscription : 09/11/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 19:56 Jeu 10 Nov 2011, 19:56 | |
| comme ça le résultat sera <4
moi je veux <2 | |
|
  | |
rimetta
Féru

 Nombre de messages : 57 Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 19:57 Jeu 10 Nov 2011, 19:57 | |
| la 2e partie on a (A) (b+d)/(a+b+d)> (b+d)/(a+b+c+d) (B) ( a+c)/(a+b+c) > ( a+c)/(a+b+c+d) mm chose pour (b+d)/(b+c+d) (C) et (a+c)/(a+c+d) (D) on faisant la somme on retrouve 2( a+b+c+d)/(a+b+c+d) < A+B+C+D ET donc - 2 > - A-B-C-D 2 > 1- (b+d)/(a+b+d) +1 - (a+c)/a+b+c) +1 - (b+d)/(b+c+d) +1- (a+c)/(a+c+d) et d'ou le resultat ( sans chebtshev  ) | |
|
  | |
aminox
Maître
 Nombre de messages : 93 Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 20:18 Jeu 10 Nov 2011, 20:18 | |
| On a : a et b deux reéls positifs tel que : a=<b
faites la différence entre (b+1)/(1+b+b^2) et (a+1)/(1+a+a^2)
Dernière édition par aminox le Jeu 10 Nov 2011, 20:37, édité 1 fois | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 20:21 Jeu 10 Nov 2011, 20:21 | |
| J'ajoute une casse tête :
a²+b²+c²=1;a^3+b^3+c^3=1
Calculez : a+b²+c^3
| |
|
  | |
rimetta
Féru

 Nombre de messages : 57 Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 20:24 Jeu 10 Nov 2011, 20:24 | |
| aminox y a surement qlq chose qui manque | |
|
  | |
aminox
Maître
 Nombre de messages : 93 Nombre de messages : 93
Age : 27
Localisation : Rabat
Date d'inscription : 05/08/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Jeu 10 Nov 2011, 20:34 Jeu 10 Nov 2011, 20:34 | |
| ahhh oui , excusez moi :
On a : a et b deux reéls positifs tel que b>=a
faites la différence entre (b+1)/(1+b+b^2) et (a+1)/(1+a+a^2) | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 | |
  | |
rimetta
Féru

 Nombre de messages : 57 Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 10:39 Ven 11 Nov 2011, 10:39 | |
| pour le casse tete on a a²+b²+c² =1 et puisque a²,b²,c²>0 donc -1<a<1 aussi b et c ona a^3 +b^3 + C¨3 - a²-b²-c² = 1-1 = 0 donc a² ( a-1) +b²( b-1) +c²(c-1= 0 on deduit alors que les 3 7odoud sont negatifs et leur somme est egale a zero donc a=0 ou a=1 ET b=0 ou b=1 ET c=1 ou c=0 et selon a²+b²+c² = 1 donc les solutions possibles sont ( 0,0, 1) , ( 1, 0, 0), ( 0 ,1, 0) dans les 3cas on a a+b²+ c^3 = 1 pour l'exo de aminox on peut mm faire la difference classique des deux cotes  | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 11:26 Ven 11 Nov 2011, 11:26 | |
| - rimetta a écrit:
- pour le casse tete
on a a²+b²+c² =1 et puisque a²,b²,c²>0 donc -1<a<1 aussi b et c
ona a^3 +b^3 + C¨3 - a²-b²-c² = 1-1 = 0
donc a² ( a-1) +b²( b-1) +c²(c-1= 0
on deduit alors que les 3 7odoud sont negatifs et leur somme est egale a zero
donc a=0 ou a=1 ET b=0 ou b=1 ET c=1 ou c=0
et selon a²+b²+c² = 1
donc les solutions possibles sont ( 0,0, 1) , ( 1, 0, 0), ( 0 ,1, 0)
dans les 3cas on a a+b²+ c^3 = 1
pour l'exo de aminox on peut mm faire la difference classique des deux cotes  Je pense >= et <= | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 11:32 Ven 11 Nov 2011, 11:32 | |
| - rimetta a écrit:
- pour le casse tete
on a a²+b²+c² =1 et puisque a²,b²,c²>0 donc -1<a<1 aussi b et c
ona a^3 +b^3 + C¨3 - a²-b²-c² = 1-1 = 0
donc a² ( a-1) +b²( b-1) +c²(c-1= 0
on deduit alors que les 3 7odoud sont negatifs et leur somme est egale a zero
donc a=0 ou a=1 ET b=0 ou b=1 ET c=1 ou c=0
et selon a²+b²+c² = 1
donc les solutions possibles sont ( 0,0, 1) , ( 1, 0, 0), ( 0 ,1, 0)
dans les 3cas on a a+b²+ c^3 = 1
pour l'exo de aminox on peut mm faire la difference classique des deux cotes  On peut trouver comme solution (-1,0,0)ou(..........)ou(1/2,V3/2,0)ou(.........) ! ! ! ! !  | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 11:34 Ven 11 Nov 2011, 11:34 | |
| La différence classique "rimetta" est insuffisante dans bcs d'exos c pqs je ne l’utilise pas | |
|
  | |
rimetta
Féru

 Nombre de messages : 57 Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 11:37 Ven 11 Nov 2011, 11:37 | |
| nn ca ne vérifie pas a^3 + b^3 + c^3 = 1 | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 12:00 Ven 11 Nov 2011, 12:00 | |
| Je nais pas la réponse; en tous cas bonne tentative ; mnt, J'ajoute les exos difficiles afin qu'on puisse bien préparer a la première Phase d'olympiades: Série 1 De la Préparation :- Spoiler:
Exercice 1 :A un point d'un cercle (C), et (Delta ) est tangente à (C) dans A, et (Delta') une autre droite qui coupe (C) dans E et F et coupe (Delta) en M. la bissectrice intérieure de \angle{AME} coupe AE et AF dans P et Q. Montrer que AP²=PE.QFExercice 2 :Combien y a t'il de diviseurs de 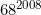 Exercice 3 : Exercice 3 :déterminer toute les fonctions f de  tel que : +y)=f(x^2&space;-y)+4yf(x)) Exercice 4 : Exercice 4 :Résoudre dans IR² le système 
P.S. : -Je ne sais aucune réponse sauf du premier -SVP Ecrivez en LaTeX Bonne chance 
Dernière édition par diablo902 le Ven 11 Nov 2011, 12:03, édité 1 fois | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 12:01 Ven 11 Nov 2011, 12:01 | |
| - rimetta a écrit:
- nn ca ne vérifie pas a^3 + b^3 + c^3 = 1
Pardon  Je n'ai pas vu  | |
|
  | |
rimetta
Féru

 Nombre de messages : 57 Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 14:00 Ven 11 Nov 2011, 14:00 | |
| c pas grave katw9a3
exo 1:
remarquons que AFM et AEM puis AQM et EPM sont deux triangles moutachabihan ( les angles y sont égaux - FÂM ET AÊM tahsorani le mm arc)
donc AM/EM =AF/AE= FM/AM
et AM/EM = QM/PM= AQ/EP
alors AF/AE = AQ/EP =( AF - AQ)/(AE-EP)
et puisque A^QP = A^PQ ( angle kharijian dans deux triangles)
dans APQ est un triangle mtassaoui saqayn : AP=AQ
et donc AQ/EP= AP/EP= QF/AP
d'ou AP²= EP * QF
EXO 2
on a 68^2008 = ( 4*17)^2008
= 2^4016 * 17^2008
DONC les diviseurs sont : 2 ,2² ,2^3 ,2^4 ,2^5 .....2^4016 et 17,17² ... 17^2008 et
2* 17 2*17² 2*17^3 et ainsi de suite jusqu'à 2*17^2008
2²* 17 2²*17² . 2² * 17^2008
. . . .
. . .
2^4016*17 2^4016*17²
et donc on retrouve 4016+2008+4016 *2008 diviseurs = 8070152 | |
|
  | |
rimetta
Féru

 Nombre de messages : 57 Nombre de messages : 57
Age : 28
Localisation : rabat
Date d'inscription : 09/10/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 14:09 Ven 11 Nov 2011, 14:09 | |
| pour les fonctions on ne les a pas encore faites | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 14:24 Ven 11 Nov 2011, 14:24 | |
| Donc rimetta if faut que tu poste 2 autres exos | |
|
  | |
oiga
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 28
Date d'inscription : 09/11/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 14:24 Ven 11 Nov 2011, 14:24 | |
| salam les amis
Réponse à l'exo 4 de la série qui nécessite pas le latex
a= xy
b= x+y
xy²+x²y=xy(x+y)=-8
xy+x+y=2
en remplaçant xy par a et x+y par b
ab=-8
a+b=2
(a+b)²=a²+2ab+b²=a²+b²-16=4 <==> a²+b²=20
(a-b)²= a²-2ab+b²=20 +16=36
a-b= 6 ou a-b= -6
nous avons
a+b=2
a-b=6 ; a-b=-6
alors le résultat (a;b) est (4;-2) ou (-2;4)
pour trouver x et y
nous avons deux situations
la première
a= 4 et b= -2
xy=4 et x+y=-2
par la même méthode utilisée avec a et b on trouvera que la première situation fausse
car on trouvera un carré négatif
la 2ème situation :
a=-2 b=4
xy=-2 et x+y=4
alors
(x+y)²=16=x²+2xy+y²=x²+y²-4
alors
x²+y²=20
(x-y)²=x²+y²-2xy=20-2xy=20+4=24
(x-y)²= V24 ou -V24
x+y= 4 | x+y=4
x-y= V24 | x-y=-V24
V24+2y=4 | 2y -V24=4
2y=4-2V6 | 2y=4+V24
y=(4-2V6)/2 = 2-V6 | y= (4+V24)/2= 2+V6
x= 4- 2+V6=2+V6 | x= 4-2-V6=2-V6
les solutions (a,b) sont (2+V6, 2-V6) ou (2-V6,2+V6)
| |
|
  | |
oiga
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 28
Date d'inscription : 09/11/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 14:33 Ven 11 Nov 2011, 14:33 | |
| La réponse est longue car elle est détaillée | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  Ven 11 Nov 2011, 14:41 Ven 11 Nov 2011, 14:41 | |
| - rimetta a écrit:
- c pas grave katw9a3
exo 1:
remarquons que AFM et AEM puis AQM et EPM sont deux triangles moutachabihan ( les angles y sont égaux - FÂM ET AÊM tahsorani le mm arc)
donc AM/EM =AF/AE= FM/AM
et AM/EM = QM/PM= AQ/EP
alors AF/AE = AQ/EP =( AF - AQ)/(AE-EP)
et puisque A^QP = A^PQ ( angle kharijian dans deux triangles)
dans APQ est un triangle mtassaoui saqayn : AP=AQ
et donc AQ/EP= AP/EP= QF/AP
d'ou AP²= EP * QF
tu peux nous donner toute l démonstration pour " et puisque A^QP = A^PQ ( angle kharijian dans deux triangles)
dans APQ est un triangle mtassaoui saqayn : AP=AQ" | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 ) Sujet: Re: Préparations aux olympiades de tronc commun (2011-2012 )  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2011-2012 ) |  |
|
