Préparations aux olympiades de tronc commun (2011-2012 )

Est ce que ma réponse a l'exo 2 est correcte
??

Oui je pense

exo 10:

c'est facile (pas pour diablo)

On a X compri entre 1 et 1+Y tel que :Y appartient à R*+

Montrez que : (VX -1)^2 est inférieure à Y^2/4

Solution de l'exercice 10

On a X<1+Y
Donc VX<V(1+Y)
Donc 2VX <2V(Y+1)
On sait que 2V(Y+1)<Y+2

D'ou 2VX <Y+2
Donc VX<Y/2 +1
Et puis VX-1<Y/2
Ainsi (VX-1)²<Y²/4
Ce qui finit la démonstration....

Bien ;allez postez quelques exo difficiles

Je n'ai pas de difficiles exo à vous poster ..
mais je vous propose celui là:
Exo 11
Déterminez n de IN de sorte que



J'espère que vous posterez la solution assez vite que possible si cela vous parait facile..

Faites la différence entre : 2^141 et 3^94

upsilon copier coller du manuel

Allez je vais vous montrer les exos difficiles :
Exercice 13 :
Comparez : a=31^11 et b=17^14

Exercice 13
voici la solution

Puisque 31<17^3
Donc 31/(17^3)<1
D'ou <1

Donc <1

Enfin 31^11<17^14

diablo902 a écrit:

upsilon copier coller du manuel

Exacte c'est copier coller du manuel, mais cela ne veut pas dire que c'est facile (selon vous)
et puis ce serait bon de poster une solution tout de même...?!

réponse à l'exo 13:

On a : 17^3 >= 2^11 [Car (1+2^4)>=2^12>=2^11]

Donc : 17^3*17^11 >= 2^11*17^11

Donc : 17^14 >= 34^11 >= 31^11

Réponse D'exo 11 :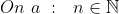

Si n=0 :
Si n>0 :
La seule solution est 0.
Sauf Erreur
Réponse d'exo 12:

Sauf Erreur

Salut: je crois que la réponse de Upsilon de l'exo 13 est fausse car 31^11/17^14 n'égalle pas (31/17^3)^11

aminox a écrit:

Salut: je crois que la réponse de Upsilon de l'exo 13 est fausse car 31^11/17^14 n'égalle pas (31/17^3)^11

Ah oui!! je m'excuse vous avez raision j'ai fait une stupide faute..

Mais cela fait de ma résolution fausse....
LA SOLUTION DE aminox est juste...

J'ajoute Un Exo
Exercice 14:
Soit a et b deux réels positifs tels que: a+b=1
Prouver que :

J'att vos exos

a²/(a+1)+ b² /(b+1)>=1/3
a²/(a+1) + b²/ (b+1) - 1/3 >=0
(a²(b+1) + b²(a+1) - (a+1)(b+1)) / (a+1)(b+1)>=0

(a+1)(b+1)= ab+a+b+1=ab+2

(a²b +a² + b²a + b² -ab -2)/ (ab+2) >=0
(a²+b²-2ab + ab +a²b+b²a)/ (ab+2) >=0
((a-b)²+ab + ab(a+b))/ (ab+2) >=0
puisque a et b sont positifs
((a-b)²+ab + ab(a+b))/ (ab+2) >=0
est juste
alors
a²/(a+1)+ b² (b+1)>=1/3

oiga a écrit:

a²/(a+1)+ b² /(b+1)>=1/3
a²/(a+1) + b²/ (b+1) - 1/3 >=0
(a²(b+1) + b²(a+1) - (a+1)(b+1)) / (a+1)(b+1)>=0

(a+1)(b+1)= ab+a+b+1=ab+2

(a²b +a² + b²a + b² -ab -2)/ (ab+2) >=0
(a²+b²-2ab + ab +a²b+b²a)/ (ab+2) >=0
((a-b)²+ab + ab(a+b))/ (ab+2) >=0
puisque a et b sont positifs
((a-b)²+ab + ab(a+b))/ (ab+2) >=0
est juste
alors
a²/(a+1)+ b² (b+1)>=1/3

Comment t'as fait ca

En utilisant la méthode classique:

b=1-a

Donc S=a^2/a+1 + b^2/b+1=a^2/a+1 + (1-a)^2/(2-a) [C'est moi qui l'est appelé S]

Et on a: S- (1/3)=3a^2-3a+2/(nombre positif) [aprés les calculs]

=3a(a-1)+2

=-3ab+2

Donc faut démontrer que 3ab=<2 <==> ab=<2/3:


a^2+b^2>=-1/3 <==> a^2+b^2-1>=-4/3

<==> 2ab=<4/3

<==> ab=<2/3

Donc: a²/(a+1)+ b² (b+1)>=1/3

Autre méthode: D'aprés l'inégalité de Tchebychey:

a(a/a+1)+b(b/b+1)>=(1/2)*(a+b)[(a/a+1)+(b/b+1)]=(1/2)*[(a/a+1)+(b/b+1)]

a(a/a+1)+b(b/b+1)>=[2ab+(1/2)]/[ab+2]

Donc faut démontrer que [2ab+(1/2)]/[ab+2]>=1/3


On a 2ab>=-1/2 <==> 3ab+3/2>=ab+2

<==> 3(ab+1/2)>=ab+2

<==> (ab+1/2)(ab+2)>=1/3


Donc a(a/a+1)+b(b/b+1)>=(ab+1/2)(ab+2)>=1/3

Donc a(a/a+1)+b(b/b+1)>=1/3

pardon une petite faute, je réécris ma réponse avec plus de détails
tafssil moumil

a²/(a+1)+ b² /(b+1)>=1/3
a²/(a+1) + b²/ (b+1) - 1/3 >=0
la somme
(3a²(b+1) + 3b²(a+1) - (a+1)(b+1)) / 3(a+1)(b+1)>=0
3(a+1)(b+1) est positif
il faut seuelment prouver que (3a²(b+1) + 3b²(a+1) - (a+1)(b+1)) >=0
3a²(b+1) + 3b²(a+1) - (a+1)(b+1)
= 3a²b+3a² + 3b²a+ 3b² - (ab+a+b+1)
= 3ab(a+b) + 3 (a²+b²) - (ab+2)
=3ab +2 (a²+b²) + (a²+b²)-ab -2
=2ab+2((a+b)²-2ab) + (a-b)²+2ab -2
= 4ab + 2 - 4ab + (a-b)² -2
= (a-b)²
Puisque (a-b)² est positif
3a²(b+1) + 3b²(a+1) - (a+1)(b+1) >=0
alors
a²/(a+1)+ b² /(b+1)>=1/3

c ce que j'ai fais dans ma premiére méthode

C la méthode classique(elle ne marche pas toujours

ma deuxiéme méthode est la méthode qui marche toujours