Une autre

Soit 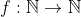une application injective telle que: .


Déterminer .

Je réponds:

On a pour n=0 : f(0)<=0 et on a f(0) £ IN alors f(0)=0
On a pour n=1 : f(1)<=1 et on a f(1) £ IN et f(1)=/=f(0) [f est injective] alors f(1)=1
On a f est injective alors f est strictement monotone et puisque 1>0 => f(1)>f(0)
alors f est croissante.
Prouvons par récurrence que f(n)=n :
Pour n=0 on a f(0)=0 .
Supposons que pour tout n on a f(n)=n et prouvons le pour n+1:
On a n+1>n alors f(n+1)>f(n) ainsi f(n+1)>n
On a f(n+1)<=n+1 alors n<f(n+1)<=n+1 et puisque f(n+1) £ IN
alors f(n+1)=n+1.

Synthèse: La seule solution est f(n)=n pour tout n de IN.

Bien.

J'ai lu les grandes lignes, ça me parait juste...

Merci...

yasserito a écrit:

Je réponds:

On a pour n=0 : f(0)<=0 et on a f(0) £ IN alors f(0)=0
On a pour n=1 : f(1)<=1 et on a f(1) £ IN et f(1)=/=f(0) [f est injective] alors f(1)=1
On a f est injective alors f est strictement monotone et puisque 1>0 => f(1)>f(0)
alors f est croissante.
Prouvons par récurrence que f(n)=n :
Pour n=0 on a f(0)=0 .
Supposons que pour tout n on a f(n)=n et prouvons le pour n+1:
On a n+1>n alors f(n+1)>f(n) ainsi f(n+1)>n
On a f(n+1)<=n+1 alors n<f(n+1)<=n+1 et puisque f(n+1) £ IN
alors f(n+1)=n+1.

Synthèse: La seule solution est f(n)=n pour tout n de IN.

Il faut signaler une récurrence forte : "pour n fixé, pour tout k <= n, on a : f(k)=k"

Soit f^(k)(n)=fofo...of(n) ( k fois )
remplacons n par f(n) : f(f(n))=<f(n)=<n.
dans la relation precedente on remplace une autre fois n par f(n) alors f^(3)(n)=<f(n)=<n.
par une réccurence On prouve que : pour tout k dans IN. f^(k)(n)=<n.
en particulier pour on a :
f^(1)(n)=<n , f^(2)(n) =<n. .... f^(n+1) =<n.
donc d'après le principe des tiroirs Il existe i>j, tels que :
f^(i)(n)=f^(j)(n). mais comme f est injective alors :
f^(i-j)(n)=n.

D'une autre part on a :
f^(i-j)(n) =<f^(i-j-1)(n) =<....=<f(n)
=> n=f^(i-j) (n) =<f(n).
n=<f(n)

et donc pour tout n dans IN f(n)=n..

Sinon il est facile de resoudre ce problème par la reccurence forte.

yasserito a écrit:

[]
On a f est injective alors f est strictement monotone et puisque 1>0 => f(1)>f(0)
alors f est croissante.
Prouvons par récurrence que f(n)=n :
Pour n=0 on a f(0)=0 .
[]

Pour une fonction discrète, ce n'est pas nécessaire que l'injectivité implique la monotonie, comme pour les fonctions continues. Par exemple, la fonction f d'entiers naturels telle que : f(0) = 1, f(1) = 0, f(2)=3, f(3)=2, f(4)=5, f(5)=4... f(2i) = 2i +1,
f(2i +1) = 2i
est injective non monotone.
Mais comme tu as poursuivi

yasserito a écrit:

Supposons que pour tout n on a f(n)=n et prouvons le pour n+1:

f(2) <= 2 mais f(2) =/= f(0), f(1). Donc f(2) = 2 et f(3) qui est <= 3 est différent de 0, 1 et 2 et donc f(3)=3
..

yasserito a écrit:

Synthèse: La seule solution est f(n)=n pour tout n de IN.