TDM - test 1 - Problème 4

Problème 4.
Soient $TDM - test 1 - Problème 4 1bd666a395a45955a30af87360ff4202a5b546c3$ et $TDM - test 1 - Problème 4 84a516841ba77a5b4648de2cd0dfcb30ea46dbb4$ des reels strictement positifs tels que $TDM - test 1 - Problème 4 D7609865020abbeddea362f6aa3fcacff5cd1c01$ . Prouver que:

$TDM - test 1 - Problème 4 705707c508f5dea6b12874de2c66f20f29d8f4f4$

Cette belle inégalité était proposée par Sporovitch, et elle n'était pas trivial du tout. Il me parait que personne n'as abouti à une solution complète. J'invite tout les forumistes à participer dans cette discusion et à partager leurs idées.

Les inégalités de Sporovotich ..
Que veux-tu qu'on y fasses xD.

Expert sup Nombre de messages : 521 Age : 29 Date d'inscription : 23/12/2010

j'ai une petite question
Si on arrive po a résoudre un exo mais qu'on avance un peu dans la démonstration , es qu’il faut envoyer nôtre résultats ?

Non vous devez par contre l'envoyer!

Féru Nombre de messages : 49 Age : 30 Date d'inscription : 26/02/2010

On peut remarquer que :
http://www.pixenli.com/image1309377178029564900.html

Expert sup Nombre de messages : 521 Age : 29 Date d'inscription : 23/12/2010

ce que j'ai pu trouver est TDM - test 1 - Problème 4 Codeco12

et

si nn utilser une inégalité: https://i.servimg.com/u/f42/16/62/75/03/codeco16.gif

Féru Nombre de messages : 49 Age : 30 Date d'inscription : 26/02/2010

à quoi sert le fait que abc=1 ?

ben ouais si tu veux prouver l'inégalité en question faut utiliser abc=1

Féru Nombre de messages : 49 Age : 30 Date d'inscription : 26/02/2010

de quelle manière l'utiliser ?

A3+b3+c3-(a²c+b²a+c²b) =(a-b)(a²-b²)+(b-c)(b²-c²) >= 0→a3+b3+c3> a²c+b²a+c²b pitetre

steve 94 a écrit:: A3+b3+c3-(a²c+b²a+c²b) =(a-b)(a²-b²)+(b-c)(b²-c²) >= 0→a3+b3+c3> a²c+b²a+c²b pitetre

et alors ? Shocked

Je pense que l'inégalité n'était pas triviale mais pas difficile j'espere voir plus de participations dans les prochains TDM
-les résultats de ce test seront affichés avec ceux du 2eme test : le DIMANCHE prochain ! .
-j'aimerai aussi voir les différentes solutions des forumistes pour cette inégalité.

Personne n'as trouvé une solution complète pour ce problème durant l'épreuve. Je vous présente ma solution en attendant les votres.
Solution.
Lemme.
Pour tous réels positifs $TDM - test 1 - Problème 4 11f6ad8ec52a2984abaafd7c3b516503785c2072$ , on a: $TDM - test 1 - Problème 4 3b28d81a879195ba3806cb6ddef993a660000ff7$
Preuve.
Trivial, elle équivaut à: $TDM - test 1 - Problème 4 625243c898516380c7e22a13c01f6a743e620d5c$

D'après le lemme on a:

$TDM - test 1 - Problème 4 774da316a094221b48860928e0babf034fc92fd4$

Donc:

$TDM - test 1 - Problème 4 8d4d4fad44feeaf1001f7f93b73f2780fca99973$ .
D'où:

$TDM - test 1 - Problème 4 21c42080575b6c7f80eddc44d66b775b0799f60a$

Et par conséquent :

$TDM - test 1 - Problème 4 705707c508f5dea6b12874de2c66f20f29d8f4f4$

L'inégalité n'était pas tellement compliqué, mais astucieuse!

Habitué Nombre de messages : 15 Age : 64 Date d'inscription : 23/06/2011

Bonsoir Sporovitch Smile

l'inego apparait chadda, à rak chaaad mon fils sporovitch !
On pose :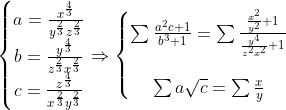
$TDM - test 1 - Problème 4 Gif.latex?\left\{\begin{matrix}%20a=\frac{x^{\frac{4}{3}}}{y^{\frac{2}{3}}z^{\frac{2}{3}}}\\%20b=\frac{y^{\frac{4}{3}}}{z^{\frac{2}{3}}x^{\frac{2}{3}}}\\%20c=\frac{z^{\frac{4}{3}}}{x^{\frac{2}{3}}y^{\frac{2}{3}}}%20\end{matrix}\right.%20\Rightarrow%20\left\{\begin{matrix}%20\sum%20\frac{a^2c+1}{b^3+1}=\sum%20\frac{\frac{x^2}{y^2}+1}{\frac{y^4}{z^2x^2}+1}\\%20\\\sum%20a\sqrt{c}=\sum%20\frac{x}{y}%20\end{matrix}\right$
ainsi l'inégalité est équivalente à :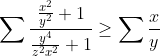
$TDM - test 1 - Problème 4 Gif$
encore une fois , changement de variables :
$TDM - test 1 - Problème 4 Gif.latex?\left\{\begin{matrix}%20m=\frac{x}{y}\\%20n=\frac{y}{z}\\%20p=\frac{z}{x}%20\end{matrix}\right.\Rightarrow%20\left\{\begin{matrix}%20\sum%20\frac{\frac{x^2}{y^2}+1}{\frac{y^4}{z^2x^2}+1}=\sum%20\frac{m^2+1}{\frac{n^2}{m^2}+1}=\sum%20\frac{m^2(m^2+1)}{m^2+n^2}\\%20\\%20mnp=1%20\end{matrix}\right$
l'inégalité devient :
$TDM - test 1 - Problème 4 Gif$
Or d'après l'inégalité de A.mehdi-G.metaich on a :
$TDM - test 1 - Problème 4 Gif$
$TDM - test 1 - Problème 4 Gif$
ainsi en sommant les deux inégalités(1) et (2), on en déduit l'inégalité demandée.
INTAHA.

Très joli solution MohE.

Ma solution :
On a l'inégalité est équivalente à : $TDM - test 1 - Problème 4 02cb7ba196f757230b32e6b50b4e3ee2056bdd7e$
a/b=x , b/c=y ; c/a=z
ce qui est vrai car : $TDM - test 1 - Problème 4 93f28cf9bc765c3c112ce930cea2db6645479ca4$

Expert sup Nombre de messages : 1665 Age : 30 Date d'inscription : 05/03/2010

Courtes et belles ! trés jolies solutions de la part de Sporovitch et MohE .
J'aime l'inégalité :p

M.Marjani a écrit:: Courtes et belles ! trés jolies solutions de la part de Sporovitch et MohE .
J'aime l'inégalité :p

La troisiàme solution -celle de Metaich.A- est aussi à la hauteur, voire plus détaillée.

» TDM - test 2 - Problème 3
» TDM - test 2 - Problème 4
» TDM - Test 3 - Problème 1
» TDM - Test 3 - Problème 2
» TDM - Test 3 - Problème 3