Ma réponse pour problème 3:Soient a, b et c des réels strictement positifs tel que: a+b+c=ab+ac+bc.
Considérons la fonction f définie sur IR+:
=\sqrt{x})
.
On a:
=-\frac{1}{4x^{\frac{3}{2}}}\leq%200\Leftrightarrow)
f est concave sur IR+.
Donc d'après Jensen:
+f(a^2+ac+c^2)+f(b^2+bc+c^2)\leq%203f(\frac{2(a^2+b^2+c^2)+(ab+ac+bc)}{3}))
+4(ab+ac+bc)-3(ab+ac+bc)}{3}))
^2-3(a+b+c)}{3}))
Donc pour montrer l'inégalité proposée, il suffit de montrer que:
^2-3(a+b+c)}{3}}\leq%20\sqrt{(a+b+c)^3})
^2-3(a+b+c)}{3})\leq%20(a+b+c)^3)
^2-9(a+b+c)\leq%20(a+b+c)^3)
Posons:
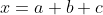
.
L'inégalité à démontrer est alors équivalente à:
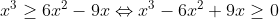
\geq%200\Leftrightarrow%20x(x-3)^2\geq%200)
Ce qui est vrai vu que:
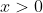
(car x=a+b+c et a,b et c sont des réels strictement positifs) et
^2\geq%200)
.
CQFD.
