| | Jeu d'Hiver 2011-2012.(préparation aux olympiade) |  |
|
+19Oty stof065 Nayssi hind nassri Ahmed Taha (bis) ryuuzaki omra ali-mes amigo-6 yasserito manazerty rimele az360 judicecharatein Misterayyoub diablo902 Mehdi.O expert_run ZYGOTO boubou math 23 participants |
|
| Auteur | Message |
|---|
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Jeu 03 Nov 2011, 22:01 Jeu 03 Nov 2011, 22:01 | |
| Comme l'indique son nom , ce sujet a pour but d'organiser un jeu pour bien se préparer aux olympiade,les règles ne sortent pas du commun : 1/ chaque problème posté devrai avoir un numéro. 2/ Les Solutions devrai être en spoiler . 3/ chaque participant ayant donné une solution à un précédent problème doit se charger de proposer un nouveau problème.si quelqu'un arrive à trouver une solution sans avoir un nouveau exercice qu'il indique pour que quelqu'un d'autre le fait . 4/ De préférence les énoncés et les solutions devraient être rédigé en Latex 5/ Ne pas poster un nouveau problème avant qu'une solution de l'ancien soit posté (sauf si un problème dépasse 4 jours sans être résolu ) Finalement, j’espère que votre participation serra serra la plus fructueuse. J'attend vos remarques. exercice N1Trouver tous les entiers premiers (a,b,c) tel que : 
Dernière édition par boubou math le Jeu 12 Jan 2012, 19:30, édité 2 fois | |
|
  | |
ZYGOTO
Féru
 Nombre de messages : 58 Nombre de messages : 58
Age : 31
Date d'inscription : 19/10/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Jeu 03 Nov 2011, 22:22 Jeu 03 Nov 2011, 22:22 | |
|
Dernière édition par ZYGOTO le Jeu 03 Nov 2011, 23:14, édité 1 fois | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Jeu 03 Nov 2011, 22:59 Jeu 03 Nov 2011, 22:59 | |
| Solution pour problème 1:
On suppose que a>=b>=c
ab+ac+bc>abc <==> 1/a + 1/b + 1/c >1
Donc 3/c >= 1/a + 1/b + 1/c > 1
Pour c>=3 Il n’existe aucune solution.
Pour c=2
1/a + 1/b + 1/c= 1/a+ 1/b +1/2 >1 <==>1/a+ 1/b > 1/2
-----Pour b>=5 2/5>= 1/a + 1/b il n'existe aucune solution
.......Pour b=3
1/a + 1/b + 1/c= 1/a+ 1/3 + 1/2 =>1/a >1/6 <==> a€{3;5}
......Pour b=2
1/a + 1/b + 1/c=1+1/a donc a€P tel que P est l ensemble des premiers positifs.
Solution:
(p,2,2) et ses permutations avec p€P et (3,3,2);(3;5;2) et leurs permutations | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Jeu 03 Nov 2011, 23:35 Jeu 03 Nov 2011, 23:35 | |
| Problème2:Soient a;b et c des réels positifs tq: a+b+c=1 Prouver que:  | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 | |
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Ven 04 Nov 2011, 14:32 Ven 04 Nov 2011, 14:32 | |
| | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 05 Nov 2011, 10:03 Sam 05 Nov 2011, 10:03 | |
| autre Solution pour exo 2 sans Jensen :- Spoiler:
L'inégalité est symétrique , sans perte de généralité , supposons que 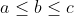 ainsi on a  avec Tchebychev (\sqrt{b+c}+\sqrt{a+c}+\sqrt{a+b})\geq&space;3(a+b+c)=3&space;\Leftrightarrow&space;\frac{a}{\sqrt{b+c}}+&space;\frac{b}{\sqrt{a+c}}+&space;\frac{c}{\sqrt{a+b}}&space;\geq&space;\frac{3}{\sqrt{b+c}+\sqrt{a+c}+\sqrt{a+b}}) d'une autre part Ac C.S ^2\leq&space;(2(a+b+c))(1+1+1)=6\Leftrightarrow&space;\sqrt{b+c}+\sqrt{a+c}+\sqrt{a+b}\leq&space;\sqrt{6}) en remplaçant dans la premier inégo on arrive a l'inégalité souhaité .
à toi Mehdi | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 05 Nov 2011, 12:09 Sam 05 Nov 2011, 12:09 | |
| Puisque personne n'a posté un exo . Je poste un: Problème 3 :- Spoiler:
x,y,z des réels positives tel que xyz=8 .Prouvez que: 
Bonne chance.  | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 05 Nov 2011, 15:00 Sam 05 Nov 2011, 15:00 | |
| Solution 3:Lemme: Démonstration: Démonstration:^2\geq&space;4(1+x^3&space;)\Leftrightarrow&space;x^2(x-2)^2\geq&space;0) Ce qui est vrai avec égalité ssi x=2. Donc: (1+y^3)}}\geq&space;4\sum&space;\frac{x^2}{(2+x^2)(2+y^2)}) Il suffit donc de prouver que: (2+y^2)}\geq&space;\frac{1}{3}) +x^2y^2+y^2z^2+z^2x^2\geq&space;72) Ce qui est immédiat par I.AG.
Dernière édition par expert_run le Sam 05 Nov 2011, 16:09, édité 1 fois | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 05 Nov 2011, 15:17 Sam 05 Nov 2011, 15:17 | |
| Problème4:Prouver que pour des entiers positifs m et n. 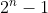 est divisible par ^2) . Si et seulement si n est divisible par ) | |
|
  | |
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 05 Nov 2011, 15:43 Sam 05 Nov 2011, 15:43 | |
| en applicaant ta lemme ta utilisé dans le dénominateur 1+x² , alors que ta lemme est pour 2+x²  je pense que ta solution est eronnée ! | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 05 Nov 2011, 16:07 Sam 05 Nov 2011, 16:07 | |
| - Misterayyoub a écrit:
- en applicaant ta lemme ta utilisé dans le dénominateur 1+x² , alors que ta lemme est pour 2+x²

je pense que ta solution est eronnée ! C'est juste une faute de frappe. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Mar 08 Nov 2011, 11:39 Mar 08 Nov 2011, 11:39 | |
| Vous pouvez voir la solution du problème 4 ici | |
|
  | |
judicecharatein
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 30
Date d'inscription : 19/09/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Mar 08 Nov 2011, 12:49 Mar 08 Nov 2011, 12:49 | |
| si expert-run le permet ,je vous propose un nouveau problème:
problème 5
trouver n tq : 2n-1 et 37n+1 soient deux carrés parfaits
Dernière édition par judicecharatein le Mar 08 Nov 2011, 21:15, édité 1 fois | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Mar 08 Nov 2011, 16:13 Mar 08 Nov 2011, 16:13 | |
| - judicecharatein a écrit:
- si expert-run le permet ,je vous propose un nouveau problème:
Probleme 5 :
trouver n tq : 2n-1 et 37n+1 soient deux carrés parfaits - Spoiler:
il faut respecter les règles "judicecharatein" : plus précisément R°1 .
| |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Jeu 10 Nov 2011, 17:59 Jeu 10 Nov 2011, 17:59 | |
| Solution du Problème 5 - Spoiler:
supposons qu'il existe deux entiers a et b tel que 37n+1=a² et 2n-1=b²
on aura ainsi 37n+1-2n+1=a²-b² --> 35n+2=a²-b² ----> 5(7n)+2=a²-b²
on remarque qu'un carré est congru 0 ou 1 ou 4 modulo
Dans tous les cas un a²-b² n'est jamais congru 2 modulo 5 ,or on a a²-b²=5(7n)+2
absurde
donc il n'existe pas n de Z vérifiant cela
Dernière édition par boubou math le Ven 11 Nov 2011, 21:48, édité 2 fois | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Jeu 10 Nov 2011, 18:46 Jeu 10 Nov 2011, 18:46 | |
| Problème 6Montrer qu'il n'existe qu'un nombre finie de triplets a,b,c d'entiers naturels tels que :  | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 09:09 Sam 12 Nov 2011, 09:09 | |
| indice : - Spoiler:
Par symétrie , supposer que a=<b=<c , un simple encadrement de a,b,c fine l'exo.
| |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 11:01 Sam 12 Nov 2011, 11:01 | |
| Par symétrie on suppose a<b<c Tchebyshev nous donne: a+b+c>=9000 encore Tchebyshev: a+b+c<=9000 Donc a+b+c=9000 Edit: Je n'ai pas b1 lire la question  Sauf erreu r J'att la confirmation pour poster un nouveau exo
Dernière édition par diablo902 le Sam 12 Nov 2011, 12:52, édité 3 fois | |
|
  | |
rimele
Féru
 Nombre de messages : 36 Nombre de messages : 36
Age : 31
Date d'inscription : 19/08/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 11:15 Sam 12 Nov 2011, 11:15 | |
| si tes démarches sont justes tu as terminer  car tu as montrer que l'ensemble des solution(non vide car le triplet (3000,3000,3000)vérifie l'équation) est borné donc fini (car il est une partie de IN) | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 12:12 Sam 12 Nov 2011, 12:12 | |
| - diablo902 a écrit:
- Par symétrie on suppose a<b<c
Tchebyshev nous donne: a+b+c>=9000
encore Tchebyshev: a+b+c<=9000
Donc a+b+c=9000
Donc (3000;3000;3000)est une solution
Sauf erreu r
J'att la confirmation pur poster un nouveau exo j'aimerais bien savoir comment tu as utilisé Tchebychev... la ligne en rouge n'a aucune relation avec l'exo , le faite que a+b+c=9000 et a,b,c sont des entier affirme qu'il n'y a qu'un nombre finie de solution . | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 12:37 Sam 12 Nov 2011, 12:37 | |
| - boubou math a écrit:
- diablo902 a écrit:
- Par symétrie on suppose a<b<c
Tchebyshev nous donne: a+b+c>=9000
encore Tchebyshev: a+b+c<=9000
Donc a+b+c=9000
Donc (3000;3000;3000)est une solution
Sauf erreu r
J'att la confirmation pur poster un nouveau exo j'aimerais bien savoir comment tu as utilisé Tchebychev...
la ligne en rouge n'a aucune relation avec l'exo , le faite que a+b+c=9000 et a,b,c sont des entier affirme qu'il n'y a qu'un nombre finie de solution . J'ai fais tchebyshev 2 fois ; la 1er (a+b+c)(1/a+1/b+1/c); la 2eme: (a+b+c)(1/c+1/b+1/a) Alors Je l'ai résolu | |
|
  | |
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 13:06 Sam 12 Nov 2011, 13:06 | |
| Bonjour tout le monde , je vous propose ma solution : Solution au probleme 6 : : (d-1000)=1000^2) Et puisque le nombre de diviseurs de 1000^2 est un nombre fini , donc on aura plusieurs systeme a resoudre , des systemes qui sont finis biensur , par conséquent on aura un nombre de solution fini aussi . CQFD sauf erreur  .
Dernière édition par Misterayyoub le Sam 12 Nov 2011, 13:55, édité 1 fois | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 13:27 Sam 12 Nov 2011, 13:27 | |
| - diablo902 a écrit:
- boubou math a écrit:
- diablo902 a écrit:
- Par symétrie on suppose a<b<c
Tchebyshev nous donne: a+b+c>=9000
encore Tchebyshev: a+b+c<=9000
Donc a+b+c=9000
Donc (3000;3000;3000)est une solution
Sauf erreu r
J'att la confirmation pur poster un nouveau exo j'aimerais bien savoir comment tu as utilisé Tchebychev...
la ligne en rouge n'a aucune relation avec l'exo , le faite que a+b+c=9000 et a,b,c sont des entier affirme qu'il n'y a qu'un nombre finie de solution . J'ai fais tchebyshev 2 fois ; la 1er (a+b+c)(1/a+1/b+1/c); la 2eme: (a+b+c)(1/c+1/b+1/a)
Alors Je l'ai résolu pourrais tu terminer la 2 eme | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 13:46 Sam 12 Nov 2011, 13:46 | |
| - Misterayyoub a écrit:
- Bonjour tout le monde , je vous propose ma solution :
Solution au probleme 6 : :
(d-1000)=1000^2)
Et puisque le nombre de diviseurs de 1000^2 est un nombre fini , donc on aura plusieurs systeme a resoudre , des systemes qui sont finis biensur , par conséquent on aura un nombre de solution fini aussi . CQFD
sauf erreur  . . l'existance d'un entier d tel que  est a prouver. De plus , à la fin tu as prouver que le nombre de solution d est finie et non pas b et c donc il te reste à prouver que pour d fixé l’équation :  admet un nombre finie de solution . | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  | |
| |
|
  | |
| | Jeu d'Hiver 2011-2012.(préparation aux olympiade) |  |
|
