| | Jeu d'Hiver 2011-2012.(préparation aux olympiade) |  |
|
+19Oty stof065 Nayssi hind nassri Ahmed Taha (bis) ryuuzaki omra ali-mes amigo-6 yasserito manazerty rimele az360 judicecharatein Misterayyoub diablo902 Mehdi.O expert_run ZYGOTO boubou math 23 participants |
|
| Auteur | Message |
|---|
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 13:48 Sam 12 Nov 2011, 13:48 | |
| - boubou math a écrit:
- diablo902 a écrit:
- boubou math a écrit:
- diablo902 a écrit:
- Par symétrie on suppose a<b<c
Tchebyshev nous donne: a+b+c>=9000
encore Tchebyshev: a+b+c<=9000
Donc a+b+c=9000
Donc (3000;3000;3000)est une solution
Sauf erreu r
J'att la confirmation pur poster un nouveau exo j'aimerais bien savoir comment tu as utilisé Tchebychev...
la ligne en rouge n'a aucune relation avec l'exo , le faite que a+b+c=9000 et a,b,c sont des entier affirme qu'il n'y a qu'un nombre finie de solution . J'ai fais tchebyshev 2 fois ; la 1er (a+b+c)(1/a+1/b+1/c); la 2eme: (a+b+c)(1/c+1/b+1/a)
Alors Je l'ai résolu pourrais tu terminer la 2 eme c'est juste ce qu'il a fait , en ce qui concene la deuxieme application de chebyshev il a inversé l'ordre parce que c l'application dans l'autre sens ( c>b>a) ( 1/c<1/b<1/a) , donc voila ca va lui donner son résultat voulu , sinon qu'en pensez vous de ma sol ? | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 13:59 Sam 12 Nov 2011, 13:59 | |
| - Misterayyoub a écrit:
- boubou math a écrit:
- diablo902 a écrit:
- boubou math a écrit:
- diablo902 a écrit:
- Par symétrie on suppose a<b<c
Tchebyshev nous donne: a+b+c>=9000
encore Tchebyshev: a+b+c<=9000
Donc a+b+c=9000
Donc (3000;3000;3000)est une solution
Sauf erreu r
J'att la confirmation pur poster un nouveau exo j'aimerais bien savoir comment tu as utilisé Tchebychev...
la ligne en rouge n'a aucune relation avec l'exo , le faite que a+b+c=9000 et a,b,c sont des entier affirme qu'il n'y a qu'un nombre finie de solution . J'ai fais tchebyshev 2 fois ; la 1er (a+b+c)(1/a+1/b+1/c); la 2eme: (a+b+c)(1/c+1/b+1/a)
Alors Je l'ai résolu pourrais tu terminer la 2 eme c'est juste ce qu'il a fait , en ce qui concene la deuxieme application de chebyshev il a inversé l'ordre parce que c l'application dans l'autre sens ( c>b>a) ( 1/c<1/b<1/a) , donc voila ca va lui donner son résultat voulu , sinon qu'en pensez vous de ma sol ? ça va donner encore a+b+c>=9000 --' | |
|
  | |
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 14:00 Sam 12 Nov 2011, 14:00 | |
| | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 14:19 Sam 12 Nov 2011, 14:19 | |
| - Spoiler:
l'existance d'un entier d tel que  est a prouver. 
| |
|
  | |
manazerty
Maître
 Nombre de messages : 123 Nombre de messages : 123
Date d'inscription : 29/06/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 14:22 Sam 12 Nov 2011, 14:22 | |
| oui c'est vrai ,il faut prouver que b+c/bc ...
Dernière édition par manazerty le Sam 12 Nov 2011, 14:47, édité 1 fois | |
|
  | |
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 14:30 Sam 12 Nov 2011, 14:30 | |
| - az360 a écrit:
- Spoiler:
l'existance d'un entier d tel que  est a prouver. 
En effet ma solution est éronnée , d appartient a Q , il ne peux pas appartenir a N pour la simple raison , si l'on prend b=c=3 , on a 1/b + 1/c = 2/3 et pas 1/d , donc voila ! je vvais penser a une autre methode Amicalement  | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 14:31 Sam 12 Nov 2011, 14:31 | |
| - Misterayyoub a écrit:
- az360 a écrit:
- Spoiler:
l'existance d'un entier d tel que  est a prouver. 
En effet ma solution est éronnée , d appartient a Q , il ne peux pas appartenir a N pour la simple raison , si l'on prend b=c=3 , on a 1/b + 1/c = 2/3 et pas 1/d , donc voila ! je vvais penser a une autre methode
Amicalement  oué,la solution de diablo902 semble aussi erronée. | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 14:37 Sam 12 Nov 2011, 14:37 | |
| Ok; Je cherche une autre en utilisant les inego aussi  | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 14:48 Sam 12 Nov 2011, 14:48 | |
| Solution pour le problème 6:
Par symétrie , on suppose que a=<b=<c
Donc 1/a +1/b +1/c =<3/a ainsi a=<3000 ( a admet un nombre fini de valeurs)
Pour a fixe:
1/a+1/b+1/c =< 1/a+2/b donc a=<b=<[2a/(1000a-1)] (b admet un nombre fini de valeurs)
Donc pour chaque valeur de a ;b admet un nombre fini de valeurs .
Pour a et b fixe il est facile de déduire que c admet une seule valeur.
Ainsi il n'existe qu'un nombre fini de triplets.
Dernière édition par expert_run le Sam 12 Nov 2011, 16:28, édité 1 fois | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 16:24 Sam 12 Nov 2011, 16:24 | |
| - expert_run a écrit:
- Solution pour le problème 6:
Par symétrie , on suppose que a=<b=<c
Donc 1/a +1/b +1/c =<3/a ainsi a=<3000 ( a admet un nombre fini de valeurs)
Pour a fixe:
1/a+1/b+1/c =< 1/a+2/b donc a=<b=<[2a/(1000a-1)] (b admet une infinité de valeurs)
Donc pour chaque valeur de a ;b admet un nombre fini de valeurs .
Pour a et b fixe il est facile de déduire que c admet une seule valeur.
Ainsi il n'existe qu'un nombre fini de triplets. pr ce qui est rouge,je pense que c'est juste une faute de frappe sinon la solution est bonne. à toi expert_run | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 16:28 Sam 12 Nov 2011, 16:28 | |
| | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 16:32 Sam 12 Nov 2011, 16:32 | |
| Problème 7:
On considère un trapèze ABCD et on suppose qu'il existe un point E de la grande base [AD] tel que les périmètres des triangles ABC;BCE et CDE sont égaux.
Démontrer que BC=1/2 AD | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 17:43 Sam 12 Nov 2011, 17:43 | |
| - expert_run a écrit:
- Problème 7:
On considère un trapèze ABCD et on suppose qu'il existe un point E de la grande base [AD] tel que les périmètres des triangles ABC;BCE et CDE sont égaux.
Démontrer que BC=1/2 AD ABE non ?!  | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 17:53 Sam 12 Nov 2011, 17:53 | |
| | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 12 Nov 2011, 22:21 Sam 12 Nov 2011, 22:21 | |
| - expert_run a écrit:
- Problème 7:
On considère un trapèze ABCD et on suppose qu'il existe un point E de la grande base [AD] tel que les périmètres des triangles ABC;BCE et CDE sont égaux.
Démontrer que BC=1/2 AD Les bases sont [AD] et [BC] ?? | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Dim 13 Nov 2011, 09:24 Dim 13 Nov 2011, 09:24 | |
| Une autre solution du problème 6 plus courte ici | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Dim 13 Nov 2011, 14:02 Dim 13 Nov 2011, 14:02 | |
| - boubou math a écrit:
- Solution du Problème 5
- Spoiler:
supposons qu'il existe deux entiers a et b tel que 37n+1=a² et 2n-1=b²
on aura ainsi 37n+1-2n+1=a²-b² --> 35n+2=a²-b² ----> 5(7n)+2=a²-b²
on remarque qu'un carré est congru 0 ou 1 ou 4 modulo
Dans tous les cas un a²-b² n'est jamais congru 2 modulo 5 ,or on a a²-b²=5(7n)+2
absurde
donc il n'existe pas n de Z vérifiant cela
Si a²=1[5] et b²=4[5] alors a²-b²=2[5]. C'est contradictoire avec ce qui est ecrit en rouge n'est ce pas? | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Dim 13 Nov 2011, 14:24 Dim 13 Nov 2011, 14:24 | |
| Solution au problème 5:
On a 2n-1=a² et 37n+1=b² et que a et b et n de Z.
On a alors a impaire alors a=2k+1 tel que k de Z
Ainsi on a n=2k²+2k+1 ainsi n est impaire car si k=0 ainsi a=1 ainsi n=1 et ainsi b²=38 impo.
On a alors 37n+1 est paire alors b est paire ainsi b=2c tel que c de Z
et ainsi 37(2k²+2k+1)+1=4c² ainsi 37(k²+k)+19=2c²
On a k²+k est paire alors 37(k²+k)+19 est impaire et on a 2c² est paire. (impossible)
Donc il n'existe aucun n de Z tel que 2n-1 et 37n+1 sont deux carres parfaits.
sauf erreur .
| |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Dim 13 Nov 2011, 15:44 Dim 13 Nov 2011, 15:44 | |
| - yasserito a écrit:
- boubou math a écrit:
- Solution du Problème 5
- Spoiler:
supposons qu'il existe deux entiers a et b tel que 37n+1=a² et 2n-1=b²
on aura ainsi 37n+1-2n+1=a²-b² --> 35n+2=a²-b² ----> 5(7n)+2=a²-b²
on remarque qu'un carré est congru 0 ou 1 ou 4 modulo
Dans tous les cas un a²-b² n'est jamais congru 2 modulo 5 ,or on a a²-b²=5(7n)+2
absurde
donc il n'existe pas n de Z vérifiant cela
Si a²=1[5] et b²=4[5] alors a²-b²=2[5]. C'est contradictoire avec ce qui est ecrit en rouge n'est ce pas? oué  | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Sam 03 Déc 2011, 22:32 Sam 03 Déc 2011, 22:32 | |
| Salut , En attente d une solution a l'exercise 5 je propose cet exercise Exercise 6: Soit (C1) et (C2) deux cercles tangentes intérieusement en un point A , de rayon respectifs R1 et R2 tel que R2=(3/4)R1 et soit M un point de (C2) tel que M differente de A La tangente à (C2) en M coupe (C1) en P et Q . Montrez que PQ= 1/2 (AP+AQ) bonne chance  | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Lun 05 Déc 2011, 21:14 Lun 05 Déc 2011, 21:14 | |
| SOLUTION DU PROBLÈME 6 - Spoiler:
- Spoiler:
d'abord , on va prouver que [AM) est la bissectrice de l'angle APQ =180-1/2(180-2\widehat{O'AM}+180-2\widehat{O'AQ})=180-180+\widehat{O'AM}+\widehat{O'AQ}=\widehat{MAQ}) ansi  ainsi,pour prouver que ) Il suffit de montrer que  Pour cela on considère l’homothétie de centre A qui envoi O à O' les point O,O'et A sont alignés,et comme (C1) et (C2) sont tangentes intérieurement en A alors  d'ou l’homothétie est de coefficient 3/4 cherchons l'image de P l'image du cercle (C) est belle est bien (C') l'image de P appretient à la droite (AP) et au cercle (C') notons l'image B l'image de P ainsi \cap&space;(PA)=\left&space;\{&space;B&space;\right&space;\}) D'ou 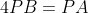 D'une autre part  d'ou le résultats demandé )
CORDIALEMENT
Dernière édition par boubou math le Jeu 12 Jan 2012, 20:05, édité 2 fois | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Mar 06 Déc 2011, 20:17 Mar 06 Déc 2011, 20:17 | |
| | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Dim 18 Déc 2011, 20:09 Dim 18 Déc 2011, 20:09 | |
|
Dernière édition par boubou math le Mer 04 Jan 2012, 18:17, édité 1 fois | |
|
  | |
ryuuzaki omra
Maître

 Nombre de messages : 164 Nombre de messages : 164
Age : 29
Localisation : Darna!
Date d'inscription : 17/12/2011
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Lun 19 Déc 2011, 21:41 Lun 19 Déc 2011, 21:41 | |
| qu'elle est la solution du problème 2
| |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  Lun 19 Déc 2011, 21:47 Lun 19 Déc 2011, 21:47 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade) Sujet: Re: Jeu d'Hiver 2011-2012.(préparation aux olympiade)  | |
| |
|
  | |
| | Jeu d'Hiver 2011-2012.(préparation aux olympiade) |  |
|
