| | Préparation Aux Olympiades 2012/2013 |  |
|
+14sadaso ZYGOTO *youness* lamperouge Soukaina Amaadour Ahmed Taha causchy schwarz 47 boubou math Thelastmetalsong9 Gauss-Maxwell k.abdo Humber alidos adeltouzani 18 participants |
|
| Auteur | Message |
|---|
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Préparation Aux Olympiades 2012/2013 Sujet: Préparation Aux Olympiades 2012/2013  Dim 02 Déc 2012, 19:11 Dim 02 Déc 2012, 19:11 | |
| Bonjour, Vu qu'il n y'avait pas de sujet visant la préparation aux olympiades de cette année pour les premières années, je me suis dis que j'en ferais un.  Donc, dans ce sujet je voudrais bien qu'on propose des exercices de préparation, inutile de poser des questions tirés du manuel ou des livres tel que dima dima ou top ... D'autre part on peut considérer ce sujet un lieu de défi... Il appartient aux membres de chercher des exercices originaux, il est possible de consulter plusieurs sources notamment de la part des professeurs, il est aussi favorable d'essayer de créer ses propres exercices, ce serait un atout quoique difficile et demande du temps  Ne participez à ce sujet que lorsque vous aurez terminer vos exercices scolaires, car les exercices proposés ici ne vous seront d'aucune aide pour les examens et D.S scolaires, conseil de la part de mon propre professeur  Finalement proposez vos solutions dans des spoilers, afin de les cacher pour les nouveaux venus, et de ne pas gâcher les exercices. N'oubliez pas de numéroter les exercices. Finalement proposez vos solutions dans des spoilers, afin de les cacher pour les nouveaux venus, et de ne pas gâcher les exercices. N'oubliez pas de numéroter les exercices.  (Essayer d'écrire en latex pour une meilleure compréhension  )
Dernière édition par adeltouzani le Dim 02 Déc 2012, 22:21, édité 2 fois | |
|
  | |
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Dim 02 Déc 2012, 19:14 Dim 02 Déc 2012, 19:14 | |
| J'ouvre ce sujet avec un exercice intéressant  Problème 1 Problème 1Chercher tous les couples (x,y) d'entiers naturels satisfaisant à l'égalité: 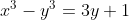
Dernière édition par adeltouzani le Dim 02 Déc 2012, 21:26, édité 1 fois | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Dim 02 Déc 2012, 20:54 Dim 02 Déc 2012, 20:54 | |
| Solution au Problème 1- Spoiler:
il suffit de remarquer que x>=y donc x=y+r avec r dans IN ainsi pour r=0 implique x=y l'équation de base n'est pas satisfaite donc r >= 1 x=y+r ainsi l'équation équivant à : 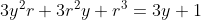 =1-r^{3}) \geq%200) 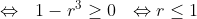 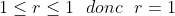 donc x=y+1 réciproquement ça donne : S={1,0}
| |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 | |
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Dim 02 Déc 2012, 22:11 Dim 02 Déc 2012, 22:11 | |
| - Spoiler:
Edit : Désolé je n'ai pas vu la première solution .
Dernière édition par Humber le Dim 02 Déc 2012, 22:21, édité 3 fois | |
|
  | |
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Dim 02 Déc 2012, 22:14 Dim 02 Déc 2012, 22:14 | |
| Solution au problème 2- Spoiler:
\in%20\mathbb{R}+*/a^{2}+b^{2}+c^{2}+abc=4) d'après l'inégalité de Cauchy Schwarz on a : (b^{2}+c^{2}+a^{2})\geq%20(ab+bc+ac)^{2}) donc : \leq%20(a^{2}+b^{2}+c^{2})) d'où: 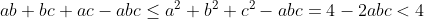 car: a,b et c des nombres strictement positifs donc la valeur maximale de 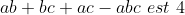
Dernière édition par adeltouzani le Dim 02 Déc 2012, 23:07, édité 5 fois | |
|
  | |
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Dim 02 Déc 2012, 22:16 Dim 02 Déc 2012, 22:16 | |
| c'est pas grave 
Dernière édition par adeltouzani le Dim 02 Déc 2012, 22:24, édité 1 fois | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Dim 02 Déc 2012, 22:23 Dim 02 Déc 2012, 22:23 | |
| - adeltouzani a écrit:
- Spoiler:
- Humber a écrit:
\text{:}(\left\%203a%20\wedge%203a+2)%20\right%20\vee%20(\left\%203a+1%20\wedge%203a)%20\right%20\vee%20(\left\%203a+2%20\wedge%203a+1)%20\right%20\\\\%20\text{On%20remplace%20mais%20on%20trouve%20que%203%20ne%20divise%20pas}%20\\%20x^3-y^3-1%20~\text{sauf%20dans%20un%20seul%20cas%20bien%20s%C3%BBr%20si%20:}%20\\x^3-y^3-1=0%20\implies(x-y)(x^2+xy+y^2)=1%20\implies%20x=y+1%20~\wedge%20~x=1%20\%20\wedge%20~y=0%20\\%20\text{(Car%20x%20et%20y%20sont%20entiers%20naturels)})
Humber, désolé mais j'ai bien demandé de mettre les solutions entre spoilers  sinon on gâche l'exercice ... tu me comprends ... Oui désolé c'est réglé  mais, je suis désolé mais tu as demandé de mettre les réponses en Spoiler Tu me comprends  | |
|
  | |
k.abdo
Féru

 Nombre de messages : 32 Nombre de messages : 32
Age : 28
Date d'inscription : 14/04/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Dim 02 Déc 2012, 22:25 Dim 02 Déc 2012, 22:25 | |
| montrer que pour tout nombre réel x : x^6 + x^4 - x^3-x + 3/4>0 | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Dim 02 Déc 2012, 22:27 Dim 02 Déc 2012, 22:27 | |
| - adeltouzani a écrit:
- Solution au problème 2
- Spoiler:
\in%20\mathbb{R}+*/a^{2}+b^{2}+c^{2}+abc=4) d'après l'inégalité de Cauchy Schwarz on a : (b^{2}+c^{2}+a^{2})\geq%20(ab+bc+ac)^{2}) donc : \leq%20(a^{2}+b^{2}+c^{2})) d'où: 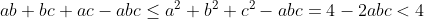 car: a,b et c des nombres strictement positifs donc la valeur maximale de 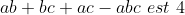
donne moi des triplets pour la quel cette valeur est atteinte sinon c'est partiellement faux . | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Dim 02 Déc 2012, 22:28 Dim 02 Déc 2012, 22:28 | |
| - k.abdo a écrit:
- montrer que pour tout nombre réel x : x^6 + x^4 - x^3-x + 3/4>0
Sans vouloir etre impoli le problème 2 est encore en Jeu . | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Dim 02 Déc 2012, 22:30 Dim 02 Déc 2012, 22:30 | |
| - k.abdo a écrit:
- montrer que pour tout nombre réel x : x^6 + x^4 - x^3-x + 3/4>0
Veuillez respecter les règles du marathon ! | |
|
  | |
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Dim 02 Déc 2012, 22:31 Dim 02 Déc 2012, 22:31 | |
| mais tu n'as pas préciser qu'on doit donner les triplets qui vérifient cette valeur  je vais m'y mettre tout de suite ... | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 | |
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 | |
  | |
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Dim 02 Déc 2012, 22:36 Dim 02 Déc 2012, 22:36 | |
| - k.abdo a écrit:
- montrer que pour tout nombre réel x : x^6 + x^4 - x^3-x + 3/4>0
Numérote cet exercice, puis essaye d'écrire en Latex ( voici un bon site: http://www.codecogs.com/latex/eqneditor.php ) c'est juste pour que tout soit en ordre  et pour ne pas se perdre par la suite, et de préférence attend qu'on poste la solution définitive d'un exercice pour pouvoir en poster un nouveau | |
|
  | |
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Dim 02 Déc 2012, 22:39 Dim 02 Déc 2012, 22:39 | |
| | |
|
  | |
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Dim 02 Déc 2012, 22:44 Dim 02 Déc 2012, 22:44 | |
| la valeur 4 est atteinte par 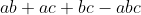 pour a=b=c=2 | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Dim 02 Déc 2012, 22:53 Dim 02 Déc 2012, 22:53 | |
| - adeltouzani a écrit:
- la valeur 4 est atteinte par
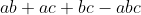 pour a=b=c=2 pour a=b=c=2 wach pour a=b=c=2 a²+b²+c²+abc=4 Pense a une Substitution trigonométrique à lire les premières pages de ce livre http://ohkawa.cc.it-hiroshima.ac.jp/AoPS.pdf/problem%20from%20the%20book.pdf  | |
|
  | |
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Dim 02 Déc 2012, 22:57 Dim 02 Déc 2012, 22:57 | |
| bessa7 j'ai oublié dak le détail ... bon merci alidos pour le livre je vais l'étudier inchaalah  | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Lun 03 Déc 2012, 18:01 Lun 03 Déc 2012, 18:01 | |
| - alidos a écrit:
- Problème 2
%3E%200%20~~~,a^{2}+b^{2}+c^{2}+abc=4%20\\~%20\\~%20Trouvez%20~~la~~valeur~~maximale%20~~de%20~~%22ab+bc+ac-abc%22) Problème 2 encore en jeu ! | |
|
  | |
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mar 04 Déc 2012, 01:25 Mar 04 Déc 2012, 01:25 | |
| Solution Problème 1 (problème 2 encore en jeu) - Spoiler:
J'ajoute ma solution seulement pour s'échanger les idées sinon le problème 2 est à priorité... voici une autre méthode: - Spoiler:
| |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mar 04 Déc 2012, 19:04 Mar 04 Déc 2012, 19:04 | |
| - adeltouzani a écrit:
- Spoiler:
Comment as-tu constaté cela !
Dernière édition par Humber le Mar 04 Déc 2012, 21:05, édité 1 fois | |
|
  | |
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mar 04 Déc 2012, 19:21 Mar 04 Déc 2012, 19:21 | |
| - Humber a écrit:
- adeltouzani a écrit:
- Spoiler:
Comment as-tu constaté cela !  Observe bien  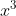 supérieur strictement à 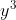 et puisque 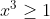 donc la seule valeur possible de y tel que 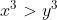 est 0  réfléchis bien on travaille dans l'ensemble 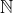 ... amicalement  | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mar 04 Déc 2012, 19:34 Mar 04 Déc 2012, 19:34 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  | |
| |
|
  | |
| | Préparation Aux Olympiades 2012/2013 |  |
|
