| | Préparation Aux Olympiades 2012/2013 |  |
|
+14sadaso ZYGOTO *youness* lamperouge Soukaina Amaadour Ahmed Taha causchy schwarz 47 boubou math Thelastmetalsong9 Gauss-Maxwell k.abdo Humber alidos adeltouzani 18 participants |
|
| Auteur | Message |
|---|
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mar 04 Déc 2012, 20:00 Mar 04 Déc 2012, 20:00 | |
| pour tous les valeurs de X, y compris 1 ... si tu vois mon raisonnement ...
| |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mar 04 Déc 2012, 20:22 Mar 04 Déc 2012, 20:22 | |
| - adeltouzani a écrit:
- pour tous les valeurs de X, y compris 1
Comment ?  | |
|
  | |
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mar 04 Déc 2012, 20:34 Mar 04 Déc 2012, 20:34 | |
| | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mar 04 Déc 2012, 21:08 Mar 04 Déc 2012, 21:08 | |
| | |
|
  | |
Gauss-Maxwell
Débutant

 Nombre de messages : 9 Nombre de messages : 9
Age : 28
Localisation : Rabat
Date d'inscription : 01/09/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mar 04 Déc 2012, 21:13 Mar 04 Déc 2012, 21:13 | |
| cette relation implique pas que la seule valeur possible de y est 0 
Dernière édition par Gauss-Maxwell le Mar 04 Déc 2012, 21:16, édité 1 fois | |
|
  | |
Thelastmetalsong9
Féru
 Nombre de messages : 49 Nombre de messages : 49
Age : 28
Localisation : xena planet
Date d'inscription : 09/11/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mar 04 Déc 2012, 21:14 Mar 04 Déc 2012, 21:14 | |
| [quote="k.abdo"]montrer que pour tout nombre réel x : x^6 + x^4 - x^3-x + 3/4>0[/quote
olympiades! :/ | |
|
  | |
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mar 04 Déc 2012, 21:19 Mar 04 Déc 2012, 21:19 | |
| | |
|
  | |
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 | |
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mar 04 Déc 2012, 21:46 Mar 04 Déc 2012, 21:46 | |
| Bah j'édite le Prob 2 il m'a était offert par un ami '' abdelkrim amine '' mais c'est vraiment pas faisable .
Problème 2
Trouver toutes les solutions positives à l'équation diophantienne : x²+21y²=10^4 | |
|
  | |
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mar 04 Déc 2012, 21:52 Mar 04 Déc 2012, 21:52 | |
| - alidos a écrit:
- Bah j'édite le Prob 2 il m'a était offert par un ami '' abdelkrim amine '' mais c'est vraiment pas faisable .
Alidos t'es sur?, si t'as la solution pose là j'aimerais bien 
Dernière édition par adeltouzani le Mar 04 Déc 2012, 21:54, édité 1 fois | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mar 04 Déc 2012, 21:54 Mar 04 Déc 2012, 21:54 | |
| Mr ''adeltouzani'' malheuresement je ne dispose pas d'une solution ,j'ai cru que c'est facile mais en vain , Désolé d'avoir bloqué le marathon .c'était involontaire  | |
|
  | |
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mar 04 Déc 2012, 22:01 Mar 04 Déc 2012, 22:01 | |
| oh ! le moins du monde d'ailleurs  on peut changer le problème 2 sous cette forme %3E0\%20a^{2}+b^{2}+c^{2}+abc=4%20~\\%20M.q:\%20ab+bc+ac-abc%3C4) où quelque chose du genre  juste une idée mais bon dans ce cas j'ai déjà posté la solution ...  | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mar 04 Déc 2012, 22:26 Mar 04 Déc 2012, 22:26 | |
| la valeur max = 2 ( sur et certain) pour la démonstration ......(loading) | |
|
  | |
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mar 04 Déc 2012, 22:34 Mar 04 Déc 2012, 22:34 | |
| c'est vrai, rien qu'en observant l'exercice on peux conjecturer que la valeur maximale est 2 ... je vais essayer cette nuit de trouver une solution  laissons cet exercice en jeu et considérons le dernier posté par toi le 3ème exo ... j'en discuterais dans tous les cas avec mon professeur | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Jeu 06 Déc 2012, 13:22 Jeu 06 Déc 2012, 13:22 | |
| - alidos a écrit:
Problème 2
Trouver toutes les solutions positives à l'équation diophantienne : (E) : x²+21y²=10^4 Solution- Spoiler:
Les solutions entières .
Si x et y sont de parité différente, il n'y a pas de solutions . Si x et y sont impairs il n'y a pas de solutions.
x et y sont donc pairs ==> x=2a , y=2b . ==> (E) <==> a²+21b²=2500.
Là aussi a et b sont pairs donc x=2a=4s et y=2b=4t ==> (E) <==> s²+21t²=625 ==> t <= 25/rac(21) ==> t <= 5
Pour t = 0 , s = 25 ==> y=0 et x=100
Pour t = 1 , pas de solutions entières
Pour t = 2 , pas de solutions entières
Pour t = 3 , pas de solutions entières
Pour t = 4 , s = 17 ==> y=16 et x=68
Pour t = 5 , s = 10 ==> y=20 et x=40
S= { (100,0) ; (68,16) ; (40,20) }
Dernière édition par Humber le Jeu 06 Déc 2012, 21:47, édité 1 fois | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Jeu 06 Déc 2012, 13:36 Jeu 06 Déc 2012, 13:36 | |
| | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Jeu 06 Déc 2012, 20:14 Jeu 06 Déc 2012, 20:14 | |
| Voici un exo facile pour relancer le marathon : Problème 3 : Résoudre dans N : 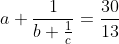 | |
|
  | |
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Jeu 06 Déc 2012, 21:09 Jeu 06 Déc 2012, 21:09 | |
| - Humber a écrit:
Si x et y sont impairs il n'y a pas de solutions.
comment ça donc ?
Dernière édition par adeltouzani le Jeu 06 Déc 2012, 22:14, édité 1 fois | |
|
  | |
causchy schwarz 47
Féru
 Nombre de messages : 38 Nombre de messages : 38
Age : 29
Date d'inscription : 11/07/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Jeu 06 Déc 2012, 21:31 Jeu 06 Déc 2012, 21:31 | |
| - Spoiler:
equ est equivalente à c/(bc+1)=(30-13a)/13 et maintenant on va resoudre le système suivant
c=30-13a et bc+1=13 --> a<=2 et bc=12 donc c appartient à {1;2;3;4;6;12} et puisque a <= 2 alors on trouve que a=2 et b=3 et c=4
;........;  amicalement
Dernière édition par causchy schwarz 47 le Jeu 06 Déc 2012, 22:08, édité 1 fois | |
|
  | |
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Jeu 06 Déc 2012, 21:41 Jeu 06 Déc 2012, 21:41 | |
| SVP respectez les règles du marathon ! on s'est bien mis d'accord sur le fait que les solutions doivent être en spoilers !! | |
|
  | |
causchy schwarz 47
Féru
 Nombre de messages : 38 Nombre de messages : 38
Age : 29
Date d'inscription : 11/07/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Jeu 06 Déc 2012, 22:06 Jeu 06 Déc 2012, 22:06 | |
| | |
|
  | |
adeltouzani
Féru

 Nombre de messages : 39 Nombre de messages : 39
Age : 29
Localisation : Casablanca
Date d'inscription : 29/06/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Jeu 06 Déc 2012, 22:14 Jeu 06 Déc 2012, 22:14 | |
| ce n'est pas grave  | |
|
  | |
causchy schwarz 47
Féru
 Nombre de messages : 38 Nombre de messages : 38
Age : 29
Date d'inscription : 11/07/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Jeu 06 Déc 2012, 22:18 Jeu 06 Déc 2012, 22:18 | |
| | |
|
  | |
causchy schwarz 47
Féru
 Nombre de messages : 38 Nombre de messages : 38
Age : 29
Date d'inscription : 11/07/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Jeu 06 Déc 2012, 22:28 Jeu 06 Déc 2012, 22:28 | |
| voilà mon exercice : 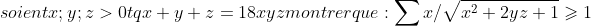 sigma cyc | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Jeu 06 Déc 2012, 22:38 Jeu 06 Déc 2012, 22:38 | |
| - adeltouzani a écrit:
- Humber a écrit:
Si x et y sont impairs il n'y a pas de solutions.
comment ça donc ? x=2a+1, y=2b+1 ==> (E) <==> 4a²+4a+84b²+84b+22=10^4 <==> 2a²+2a+42b²+42b+11=5000. Impossible ! | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  | |
| |
|
  | |
| | Préparation Aux Olympiades 2012/2013 |  |
|
