| | Préparation Aux Olympiades 2012/2013 |  |
|
+14sadaso ZYGOTO *youness* lamperouge Soukaina Amaadour Ahmed Taha causchy schwarz 47 boubou math Thelastmetalsong9 Gauss-Maxwell k.abdo Humber alidos adeltouzani 18 participants |
|
| Auteur | Message |
|---|
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mer 12 Déc 2012, 22:21 Mer 12 Déc 2012, 22:21 | |
| Probleme 17 :
trouver tous les entiers positifs x,y et z tels que x^2+y^2+z^2=1993 et x+y+z un carre parfait. | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Jeu 13 Déc 2012, 18:26 Jeu 13 Déc 2012, 18:26 | |
| Avec Caushy Schwartz : 3(x²+y²+z²) >= (x+y+z)^2 ==> x+y+z =< 77 Il est clair que x+y+z est impair , donc : x+y+z=1 ou x+y+z=9 ou x+y+z=25 ou x+y+z=49 Les trois premiers cas étant déjà impossibles il ne reste que le quatrième . Il revient de résoudre le système : x²+y²+z² = 1993 x+y+z=49 Ce dernier n'accepte pas de solutions positives  Il n'y a donc pas d'entiers positifs x,y,z tel que x^2+y^2+z^2=1993 et x+y+z est un carre parfait | |
|
  | |
Gauss-Maxwell
Débutant

 Nombre de messages : 9 Nombre de messages : 9
Age : 28
Localisation : Rabat
Date d'inscription : 01/09/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Jeu 13 Déc 2012, 19:26 Jeu 13 Déc 2012, 19:26 | |
| - Humber a écrit:
- Avec Caushy Schwartz :
3(x²+y²+z²) >= (x+y+z)^2
==> x+y+z =< 77
Il est clair que x+y+z est impair , donc :
x+y+z=1
ou x+y+z=9
ou x+y+z=25
ou x+y+z=49
Les trois premiers cas étant déjà impossibles il ne reste que le quatrième .
Il revient de résoudre le système :
x²+y²+z² = 1993
x+y+z=49
Ce dernier n'accepte pas de solutions positives 
Il n'y a donc pas d'entiers positifs x,y,z tel que x^2+y^2+z^2=1993 et x+y+z est un carre parfait pk x+y+z est impaire ?!! | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Jeu 13 Déc 2012, 19:36 Jeu 13 Déc 2012, 19:36 | |
| - Gauss-Maxwell a écrit:
- Humber a écrit:
- Avec Caushy Schwartz :
3(x²+y²+z²) >= (x+y+z)^2
==> x+y+z =< 77
Il est clair que x+y+z est impair , donc :
x+y+z=1
ou x+y+z=9
ou x+y+z=25
ou x+y+z=49
Les trois premiers cas étant déjà impossibles il ne reste que le quatrième .
Il revient de résoudre le système :
x²+y²+z² = 1993
x+y+z=49
Ce dernier n'accepte pas de solutions positives 
Il n'y a donc pas d'entiers positifs x,y,z tel que x^2+y^2+z^2=1993 et x+y+z est un carre parfait pk x+y+z est impaire ?!! x²+y²+z² et x+y+z ont la même parité  .. Et puisque x²+y²+z² = 1993 , x+y+z est ? | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Jeu 13 Déc 2012, 19:41 Jeu 13 Déc 2012, 19:41 | |
| - Humber a écrit:
- Avec Caushy Schwartz :
3(x²+y²+z²) >= (x+y+z)^2
==> x+y+z =< 77
Il est clair que x+y+z est impair , donc :
x+y+z=1
ou x+y+z=9
ou x+y+z=25
ou x+y+z=49
Les trois premiers cas étant déjà impossibles il ne reste que le quatrième .
Il revient de résoudre le système :
x²+y²+z² = 1993
x+y+z=49
Ce dernier n'accepte pas de solutions positives 
Il n'y a donc pas d'entiers positifs x,y,z tel que x^2+y^2+z^2=1993 et x+y+z est un carre parfait Joli mai kan ymken tgoul (x+y+z)^2>x^2+y^2+z^2 ou ghadi tkemel blli x+y+z>45 | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Jeu 13 Déc 2012, 19:44 Jeu 13 Déc 2012, 19:44 | |
| - Ahmed Taha a écrit:
- Humber a écrit:
- Avec Caushy Schwartz :
3(x²+y²+z²) >= (x+y+z)^2
==> x+y+z =< 77
Il est clair que x+y+z est impair , donc :
x+y+z=1
ou x+y+z=9
ou x+y+z=25
ou x+y+z=49
Les trois premiers cas étant déjà impossibles il ne reste que le quatrième .
Il revient de résoudre le système :
x²+y²+z² = 1993
x+y+z=49
Ce dernier n'accepte pas de solutions positives 
Il n'y a donc pas d'entiers positifs x,y,z tel que x^2+y^2+z^2=1993 et x+y+z est un carre parfait
Joli mai kan ymken tgoul (x+y+z)^2>x^2+y^2+z^2 ou ghadi tkemel blli x+y+z>45
Ah oui ^^ . C'est mieux . | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Jeu 13 Déc 2012, 20:00 Jeu 13 Déc 2012, 20:00 | |
| nous attons un exo khay Humber  | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 | |
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Jeu 13 Déc 2012, 22:14 Jeu 13 Déc 2012, 22:14 | |
| Solution du Problème 18- Spoiler:
lemme :un carré est Toujours congru a 0 modulo 3 ou à 1 modulo 3
Ainsi p^3=p²+q²+r² on a p^3>0 donc p>0
Premier cas : si p²=0[3] alors p^3=0[3] donc q²=0[3] et r²=0[3]
comme (p,q,r) sont premiers alors p=q=r=3 ou p=3 , q=-3 , r=-3 ou bien p=3 , q=-3 , r=3 ou bien p=3 ,q=3 ,r=-3
Deuxième cas: si p²=1[3] alors p^3=1[3] alors Again q²=0[3] et r²=0[3]
donc (q,r)=(3,3) ou (-3,-3) ou (3,-3) ou (-3,3)
Ainsi l'équation de base : p^3 -p²=18 donc p²(p-1)=18
en prenant en compte que p est premier cela donne p²=9 et p-1=2 donc p=3
Finalement , S={(3,3,3) , (3,-3,-3) ,(3,-3,3) , (3,3,-3) }
| |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Jeu 13 Déc 2012, 22:32 Jeu 13 Déc 2012, 22:32 | |
| Et je n'ai pas de problème à proposer. Que chacun se sente libre d'en proposer un à ma place.
| |
|
  | |
sadaso
Maître
 Nombre de messages : 92 Nombre de messages : 92
Age : 29
Date d'inscription : 23/06/2011
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Ven 14 Déc 2012, 17:12 Ven 14 Déc 2012, 17:12 | |
| Soit a un réel . Soit f :R=>R telle que , pour tout réel x :
f(x+a)=1/2+Racine (f(x)-[f(x)]² )
1) Prouver que f est périodique
2) Trouvez toutes les fonctions f | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Sam 15 Déc 2012, 16:19 Sam 15 Déc 2012, 16:19 | |
| Le problème 19 est l'exercice 5 de L'IMO 1968. Voici le problème 20 : 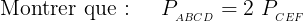 | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Lun 17 Déc 2012, 09:19 Lun 17 Déc 2012, 09:19 | |
| | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Lun 17 Déc 2012, 09:24 Lun 17 Déc 2012, 09:24 | |
| problème 21 :
determiner tous les entiers naturels x,y et z tels que : x²+y²+z²=2xyz | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mar 18 Déc 2012, 19:32 Mar 18 Déc 2012, 19:32 | |
| x²+y²+z²=2xyz (1) x²+y²+z² est pair ==> x,y,z sont pairs ou x,y pairs et z impair . Ainsi : 2xyz ≡ 0 (mod 4) ==> x²+y²+z² ≡ 0 (mod 4) ==> x,y,z sont tous pairs . De là on peut poser x=2a , y=2b z=2c (1) <==> a²+b²+c²=4abc ==> a,b,c sont pairs Donc (1) <==> r²+s²+t²=8rst avec 2r=a , 2s=b , 2t=c ... Et à leurs tours ils sont pairs. Et ainsi de suite ça ne finira jamais. Il n'y a donc qu'une seule solution si x=y=z=0. PS : on peut traiter ça d'une autre manière : ( 0 , 0 , 0 ) est une solution, supposons que (a,b,c) £ N* On a a²+b²+c² >= ab+bc+ac ==> 1/a+1/b+1/c <4 ==> (a,b,c) > 2 et 1/r+1/s+1/t <8 ==> (r,s,t) > 0 . Ca ne finira jamais aussi car pour que ça finisse un d'eux doit être impair ce qui est impossible  | |
|
  | |
Soukaina Amaadour
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 27
Localisation : Casablanca, Maroc
Date d'inscription : 13/10/2011
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Ven 28 Déc 2012, 23:13 Ven 28 Déc 2012, 23:13 | |
| Problème 22:(assez facile mais bon pour ne pas arrêter le jeu.)Montrez que : \notin&space;\mathbb{N}) Somme de k=1 jusqu'à k=n. | |
|
  | |
Gauss-Maxwell
Débutant

 Nombre de messages : 9 Nombre de messages : 9
Age : 28
Localisation : Rabat
Date d'inscription : 01/09/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Lun 31 Déc 2012, 18:01 Lun 31 Déc 2012, 18:01 | |
| on a 1/n+ 1/n+1 = 2n²+1/n²(n+1) nombre impair sur pair , donc appartient pas à n , soit Un la suite définie par Un= 1/n+1/n+1 , en donnant à n des valeur et en sommant on obtient le résultat ,( puisque on peut pas sommer "ma9amate mokhtalifa" ) | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Lun 31 Déc 2012, 19:12 Lun 31 Déc 2012, 19:12 | |
| - Gauss-Maxwell a écrit:
- on a 1/n+ 1/n+1 = 2n²+1/n²(n+1) nombre impair sur pair , donc appartient pas à n , soit Un la suite définie par Un= 1/n+1/n+1 , en donnant à n des valeur et en sommant on obtient le résultat ,( puisque on peut pas sommer "ma9amate mokhtalifa" )
Ta démo est extrêmement FLOUE ! Prière de l'éclaircir | |
|
  | |
Gauss-Maxwell
Débutant

 Nombre de messages : 9 Nombre de messages : 9
Age : 28
Localisation : Rabat
Date d'inscription : 01/09/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mar 01 Jan 2013, 12:29 Mar 01 Jan 2013, 12:29 | |
| - Humber a écrit:
- Gauss-Maxwell a écrit:
- on a 1/n+ 1/n+1 = 2n²+1/n²(n+1) nombre impair sur pair , donc appartient pas à n , soit Un la suite définie par Un= 1/n+1/n+1 , en donnant à n des valeur et en sommant on obtient le résultat ,( puisque on peut pas sommer "ma9amate mokhtalifa" )
Ta démo est extrêmement FLOUE ! Prière de l'éclaircir j'ai montré que la somme de 1/n +1/n+1 appartient pas à IN , (1/n+1/n+1= 2n²1 (nombre impair) sur n(n+1) nombre pair ! , donc en considérant la suite Un = (1/n)+(1/n+1) U_1= 1+1/2 appartient pas à IN , U_2= 1/2+1/3 appartient pas à IN ..... à Un-1 = 1/n-1 + 1/n appartient pas à IN , et puisque "lma9amate moukhtalifa " la somme des résultat appartient pas à IN ! desolé je ne maîtrise pas le latex | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mer 02 Jan 2013, 01:00 Mer 02 Jan 2013, 01:00 | |
|
Dernière édition par alidos le Mer 02 Jan 2013, 02:24, édité 5 fois | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Mer 02 Jan 2013, 01:13 Mer 02 Jan 2013, 01:13 | |
| Problème 23
A partir des chiffres 1,2,...,9 on écrit tout les nombres formés par ces neuf chiffres (les neuf chiffres sont tous distincts) puis on les ordonne par ordre croissant comme suit:
123456789, 123456798,...., 987654321.
Quel est le nombre dont le rang est 100000. | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Dim 20 Jan 2013, 18:29 Dim 20 Jan 2013, 18:29 | |
| Inégalité : (a,b,c)>=0 tel que abc=8 Prouver que : (1+b^3)}}+\frac{b^2}{\sqrt{(1+b^3)(1+c^3)}}+\frac{c^2}{\sqrt{(1+c^3)(1+a^3)}}%20\geq%20\frac{4}{3}) | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Lun 21 Jan 2013, 12:39 Lun 21 Jan 2013, 12:39 | |
| ma solution pour l'inégalité : il suffit d'utilisé l'estimation suivante qui s'obtient facilement par AM-GM /  ou z>=0 le reste est facile ..... | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Lun 21 Jan 2013, 18:20 Lun 21 Jan 2013, 18:20 | |
| | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  Lun 21 Jan 2013, 19:52 Lun 21 Jan 2013, 19:52 | |
| - legend-crush a écrit:
- Wi, c plutot facile
Legend Crush , tu n'a qu'à proposer une suite de la démo ^^ | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparation Aux Olympiades 2012/2013 Sujet: Re: Préparation Aux Olympiades 2012/2013  | |
| |
|
  | |
| | Préparation Aux Olympiades 2012/2013 |  |
|
