| | Préparation olympiades 2013 |  |
|
|
| Auteur | Message |
|---|
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Préparation olympiades 2013 Sujet: Préparation olympiades 2013  Mer 29 Fév 2012, 20:00 Mer 29 Fév 2012, 20:00 | |
| Bonsoir j ouvre la préparation avec un exercise :
Exercise1:
trouver tous f(x) sachant que : R->R
xf(x)-yf(y)=(x-y)f(x+y) | |
|
  | |
ryuuzaki omra
Maître

 Nombre de messages : 164 Nombre de messages : 164
Age : 29
Localisation : Darna!
Date d'inscription : 17/12/2011
 |  Sujet: Re: Préparation olympiades 2013 Sujet: Re: Préparation olympiades 2013  Jeu 01 Mar 2012, 20:13 Jeu 01 Mar 2012, 20:13 | |
| Salamoalikum xf(x)-yf(y)=(x-y)f(x+y) <=> xf(x)-yf(y)= xf(x+y)-yf(x+y) <=>x(f(x)-f(x+y))=y(f(y)-f(x+y)) <=> (f(x)-f(x+y))*(x+y)=0 <=> x=y ou f(x)=f(x+y) f(x)=f(y) ou f(x)=f(x+y) Je crois que c bon! Y a t-il des fautes, veuillez me les corriger Merci  | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Préparation olympiades 2013 Sujet: Re: Préparation olympiades 2013  Jeu 01 Mar 2012, 20:42 Jeu 01 Mar 2012, 20:42 | |
| - ryuuzaki omra a écrit:
- Salamoalikum
xf(x)-yf(y)=(x-y)f(x+y) <=> xf(x)-yf(y)= xf(x+y)-yf(x+y)
<=>x(f(x)-f(x+y))=y(f(y)-f(x+y)) <=> (f(x)-f(x+y))*(x+y)=0
<=> x=y ou f(x)=f(x+y)
f(x)=f(y) ou f(x)=f(x+y)
Je crois que c bon! Y a t-il des fautes, veuillez me les corriger
Merci  Bonsoir! Pourrais tu réviser la ligne: x(f(x)-f(x+y))=y(f(y)-f(x+y)) <=> (f(x)-f(x+y))*(x+y)=0 ca parrait fausse et puis tu devrais me citer toutes les fonctions f(x) possible au lieu de me donner f(x) en fonction de f(x+y) faut la donner en fonction de x ou C (constante) Good luck!!  | |
|
  | |
ryuuzaki omra
Maître

 Nombre de messages : 164 Nombre de messages : 164
Age : 29
Localisation : Darna!
Date d'inscription : 17/12/2011
 |  Sujet: Re: Préparation olympiades 2013 Sujet: Re: Préparation olympiades 2013  Jeu 01 Mar 2012, 20:48 Jeu 01 Mar 2012, 20:48 | |
| wé c vrai elle est fausse sorry faute d’inattention.  | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Préparation olympiades 2013 Sujet: Re: Préparation olympiades 2013  Jeu 01 Mar 2012, 20:50 Jeu 01 Mar 2012, 20:50 | |
| | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparation olympiades 2013 Sujet: Re: Préparation olympiades 2013  Sam 31 Mar 2012, 00:05 Sam 31 Mar 2012, 00:05 | |
| On pose : P(x,y) l'assertion : xf(x)-yf(y)=(x-y)f(x+y) . de P(x,-x) on obtient f(x)+f(-x)=c (*) quelque soit x (avec c une constante réel) . de P(1-x,-1) on obtient : (1-x)f(1-x)+f(-1)=(2-x)f(-x)quelque soit x dans R . Ainsi de la relation (*) on obtient une nouvel assertion : A(x): (1-x)f(1-x)+(2-x)f(x)=ax+b (avec a et b des constante réels) . en combinant A(1-x) et A(x) on arrive a isolé le f(x) ; ceci revient a f(x) [x(1-x)-(x-x²+2)]=a(1-3x)-2bx d'ou f(x)=tx+u quelque soit x (avec t,u appartient a R) qui vérifie l' EF .
.
Dernière édition par Oty le Mar 03 Avr 2012, 21:13, édité 1 fois | |
|
  | |
hind nassri
Maître

 Nombre de messages : 143 Nombre de messages : 143
Age : 29
Date d'inscription : 25/01/2011
 |  Sujet: Re: Préparation olympiades 2013 Sujet: Re: Préparation olympiades 2013  Sam 31 Mar 2012, 14:52 Sam 31 Mar 2012, 14:52 | |
| voici un exercice d'olympiades EXERCICE 2 a, b ,c >=0 prouver que a²+b²+c²+2abc+1>= 2(ab+bc+ac) BONNE CHANCE  | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparation olympiades 2013 Sujet: Re: Préparation olympiades 2013  Sam 31 Mar 2012, 16:10 Sam 31 Mar 2012, 16:10 | |
| lol ; un ami vient de me proposer cette exercice ce matin , voici ma démo : l'inégalité est équivalente a : (a-b)²+2c(a-1)(b-1)+(c-1)² >=0 , posant mnt : a=x+1 , b=y+1 , c=z+1 l'inégalité est une nouvel fois équivalente a : x²+y²+z²+2xyz >=0 , avec x >= -1 , y>=-1 ,z>=-1 . si x,y,z>0 l'inégalité est vérifier , si les trois sont négatif ou et l'un des trois est négatif , puisque l'inégalité est symétrique , il suffit d'étudier le cas ou : xy >0 et -1<z<0 on a : x²+y²+z²+2xyz >=x²-2xy+y²+z²=(x-y)²+z² >=0 , d'ou le résultat , sauf erreur .... | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparation olympiades 2013 Sujet: Re: Préparation olympiades 2013  Lun 02 Avr 2012, 19:22 Lun 02 Avr 2012, 19:22 | |
| Exercice 3: trouver toute les fonctions : 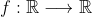 tel que : )=f(yf(x))-x^2) , 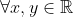 . | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Préparation olympiades 2013 Sujet: Re: Préparation olympiades 2013  Mar 03 Avr 2012, 10:55 Mar 03 Avr 2012, 10:55 | |
| - Oty a écrit:
- lol ; un ami vient de me proposer cette exercice ce matin , voici ma démo : l'inégalité est équivalente a : (a-b)²+2c(a-1)(b-1)+(c-1)² >=0 , posant mnt : a=x+1 , b=y+1 , c=z+1 l'inégalité est une nouvel fois équivalente a : x²+y²+z²+2xyz >=0 , avec x >= -1 , y>=-1 ,z>=-1 . si x,y,z>0 l'inégalité est vérifier , si les trois sont négatif ou et l'un des trois est négatif , puisque l'inégalité est symétrique , il suffit d'étudier le cas ou : xy >0 et -1<z<0 on a : x²+y²+z²+2xyz >=x²-2xy+y²+z²=(x-y)²+z² >=0 , d'ou le résultat , sauf erreur ....
Si tu la trouvée tout seul , Bravo ! En fait (a-b)²+2c(a-1)(b-1)+(c-1)² >=0 suffit pour conclure. Car il existe toujours entre a,b et c 2 nombres qui seront soit tous les 2 inférieurs à 1 soit tous les 2 supérieurs à 1 , par symetrie , on suppose que c'est a et b d'où la conclusion . | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparation olympiades 2013 Sujet: Re: Préparation olympiades 2013  Mar 03 Avr 2012, 19:01 Mar 03 Avr 2012, 19:01 | |
| Merci , Sporovitch  | |
|
  | |
Nas8
Féru
 Nombre de messages : 55 Nombre de messages : 55
Age : 28
Date d'inscription : 26/11/2011
 |  Sujet: Re: Préparation olympiades 2013 Sujet: Re: Préparation olympiades 2013  Lun 22 Avr 2013, 22:44 Lun 22 Avr 2013, 22:44 | |
| Je ne sais pas si c'est juste mais j'ai utiliser réeordonnement et j'ai trouvé :
ab c + 1x1 + b ac > ab +bc + ca et on a a² + b² +c² > ab +bc +ca ( a² + b² > 2ab ... )
donc on sommant on trouve l'inégalité posée | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparation olympiades 2013 Sujet: Re: Préparation olympiades 2013  | |
| |
|
  | |
| | Préparation olympiades 2013 |  |
|
