| | Marathon De Géométrie |  |
|
+22Oty SM.OMAR yasserito az360 boubou math momo1729 maths_lady diablo902 ali-mes SarakZit.A King Dijkschneier Bensouda majdouline Mehdi.O darkpseudo Sylphaen Sporovitch MohE nmo extrajijo Mr.Wajih 26 participants |
|
| Auteur | Message |
|---|
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Ven 11 Fév 2011, 14:29 Ven 11 Fév 2011, 14:29 | |
| Solution du problème 8 : - Spoiler:
 On dessine les segment NO , PO , MO , QO on a I,Q,N,O cocyclique car OIQ=ONQ = pi/2 de même I,M,P,O cocyclique donc : <ONI = <OQI et OMI = OPI de plus ONI = OMI vu que OM = ON = r On a alors OPI = OQI ( à partir de là on peu soit faire la puissance d'un point soit continué avec des truc simple ) , je préfère la simplicité donc le triangle OPQ est isocèle et dans un triangle isocèle la médiatrice et la médiane ne font qu'une alors IP = IQ et vu que IA=IB alors AP=BQ
Problème 9 : ABC un triangle ayant <BAC = 60 , AP la bissectrice de BAC et et BQ est la bissectrice de ABC avec P appartenant à BC et Q appartenant à AC Si AB+BP=AQ+QB quelles sont les angles du triangle ABC | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Jeu 24 Fév 2011, 21:52 Jeu 24 Fév 2011, 21:52 | |
| Ce n'est pas AP+BP=AQ + BQ? Amicalemetn  | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Sam 26 Fév 2011, 18:10 Sam 26 Fév 2011, 18:10 | |
| Voici un nouveau exo pour remplacer l'autre qui est en effet un exo de l'OIM 01 ..
Problème 9 :
Soit (C) et (C') deux cercles tangent intérieurement en un point A de Rayon R et R' t.q 4R'=3R .
M est un point de (C') différent de A . La tangente de (C') en M coupe (C) en P et Q .
Démontrer que (AM) est la bissectrice intérieure de l'angle PÂQ et que AP+AQ=2PQ | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Sam 26 Fév 2011, 19:46 Sam 26 Fév 2011, 19:46 | |
| Solution Problème 9: - Spoiler:
soit X l'intersection de (AQ) avec (C')
SOit Y l'intersection de (AP) avec (C')
SOi O ,O' les centres de (C) et (C')
il est clairement vrai A,O',O sont allignés
Soit l'homothétie de centre A qui renvoie O' à O cette homothétie renvoie (C') à (C) ce qui permet de dire que (O'Y)//(OP) car [AO']/[AO]=[AY]/[AP]
donc <AO'Y=<AOP=1/2 (<AXY)=1/2(<AQP) ==> (XY)//(PQ)
et on a : <AYM=<AMQ
et <YMA=<YXA=<PQA ==> les 2 triangles YAM et MAQ sont semblables
ce qui permet de conclure .
-Pour montrer que AP+AQ=2PQ il suffira de remarquer que AX/AQ=AY/AP=3/4
donc PY.PA=PM²=1/4 (PA²)
de meme QX.AQ=QM²=1/4(AQ)²
donc 2(QM+PM)=AP+AQ =2PQ
sauf erreur . je n'ai pas pour l'instant des problèmes intressants ! | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Sam 26 Fév 2011, 19:52 Sam 26 Fév 2011, 19:52 | |
| C'est bizzare, j'ai refait le schéma 4 fois. [AM) est extérieure à l'angle PÂQ.
| |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Sam 26 Fév 2011, 19:54 Sam 26 Fév 2011, 19:54 | |
| Je Fais déjà la première question , je terminerai la seconde demain  : Solution : - Spoiler:
 On a <MCA = <AMP , AC est la bissectrice INTERIEUR de <PAQ on ce propose de montrer que [AC ]et [AM] sont perpendiculaire : On a les triangle ACM et ATM sont semblables ( T et l'intersection de MP et AC ) donc <AMP = <MAT vu que (MP) est une tangente du cercle , le résultats s'en suit . La seconde question est en rapport avec les rayons je pense mais là je dois parti j'essairai avec demain , bonne nuit .
| |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Sam 26 Fév 2011, 20:03 Sam 26 Fév 2011, 20:03 | |
| - Mehdi.O a écrit:
- C'est bizzare, j'ai refait le schéma 4 fois. [AM) est extérieure à l'angle PÂQ.
Les 2 cercles sont tangents intérieurement ! Problème 10 :Soit ABC un triangle , M un point de [AB] et N un point de [BC] tel que : 2CN.AB=AM.BC Soit P un point de [AC] Démontrer que : (MN)et (NP) sont perpendiculaires si et seulment si (PN) est la bissectrice de <MPC
Dernière édition par Sporovitch le Sam 26 Fév 2011, 21:01, édité 2 fois | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Sam 26 Fév 2011, 20:09 Sam 26 Fév 2011, 20:09 | |
| Oups demain je verrais avec ça doit pas être bien différent ( enfin j'espère ) et wakha fike ntaya . | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Dim 27 Fév 2011, 16:05 Dim 27 Fév 2011, 16:05 | |
| Solution au problème 10:Montrons d'abord la 1ere implication : MNP est un triangle rectangle => (PN) est bissectrice de l'angle <MPC: On a cos(<MPN)=NP/MP. En utilisant la loi du sinus dans les triangles AMP et NPC, on trouve : sinA/MP=sinAPM/AM et sinC/NP=sinNPC/NC. ainsi cosMPN=(NC.sinC.sinAPM)/(AM.sinNPC.sinA)=1/2sinC/sinA.BC/AB.sinAPM/sinNPC=1/2sinAPM/sinNPC. Et on sait que APM=180°-(NPC+MPN) donc sinAPM=sin(NPC+MPN)=sinNPC.cosMPN+sinMPN.cosNPC en remplacant on trouve : cosMPN.sinNPC=sinMPN.cosNPC=> tan NPC=tan MPN il s'ensuit que [PN) est bissectric de l'angle MPC Maintenant montrons la deuxieme implication: [PN) est bissectrice de l'angle MPC => MPN rectangle: Nous avons sinAPM=sin(180°-APM)=sin(2MPN)=2sinNPC.cos MPN ainsi cos MPN=1/2sinAPM/sinNPC, et d'après ce qui est en desous : cos MPN=NP/MP, ainsi MPN est triangle rectangle. Ce qui achève la preuve  Problème 11: Problème 11:Soit ABC un triangle rectangle en A, une droite (D) perpendiculaire à (BC) coupe (AB) en M, et (AC) en N. Les cercles circonscrits de BNC et BMC coupent respectivement (AB) en P et (AC) en Q. Montrer que l'angle <PQM reste constant quand (D) change | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Dim 27 Fév 2011, 19:11 Dim 27 Fév 2011, 19:11 | |
| Solution : - Spoiler:
On a : BMD et BAC sont semblables donc : AMN et BAC sont semblables aussi , De plus on a <BCA = <NPA Et donc ABC et APN sont semblables mais dans ce cas on a donc : AMN et APN sont isométriques . On en conclu que l'angle <PNM = 2<ABC On a aussi <BCA=<BMQ et <CBM=<CQM et donc ces deux triangleS sont semblables donc AMN et AMQ sont aussi semblables et vu qu'ils on un segment en commun ils sont isométrique , or AMN et APN sont aussi isométrique on en conclu que PNMQ est un losange donc <PQM=<PNM =2<ABC CQFD . Sauf erreur . 
Problème 12 : ABC un triangle Soit ABQP et ACDE deux carrés éxtérieur au triangle soit I le milieu de BC et N et M les point d'intersections des diagonal des carrés MQ le triangle IMN est réctangle et Isocèle en I | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Lun 28 Fév 2011, 13:13 Lun 28 Fév 2011, 13:13 | |
| C'est très classique comme exo .. La rotation de centre A et d'angle 90°envoie C en E et P en B d'où
CP=BE et (CP) et (BE) sont perpendiculaire . D'après le théorème de Thalès on a :
2IN=CP et (IN)//(CP) de même 2IM=BE et (IM)//(BE) et le résultat en découle ..
Problème 13 :
ABC est un triangle est (C) sont cercle circonscrit . La tangente à (C) en A coupe BC en P . Soit M le milieu de [AP] et R la deuxième intersection de de BM et (C) . la droite PR coupe (C) en R et S . Démontrer que AP et CS sont parallèles . | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Lun 28 Fév 2011, 17:57 Lun 28 Fév 2011, 17:57 | |
| - darkpseudo a écrit:
- Solution :
- Spoiler:
On a : BMD et BAC sont semblables donc : AMN et BAC sont semblables aussi , De plus on a <BCA = <NPA Et donc ABC et APN sont semblables mais dans ce cas on a donc : AMN et APN sont isométriques . On en conclu que l'angle <PNM = 2<ABC On a aussi <BCA=<BMQ et <CBM=<CQM et donc ces deux triangleS sont semblables donc AMN et AMQ sont aussi semblables et vu qu'ils on un segment en commun ils sont isométrique , or AMN et APN sont aussi isométrique on en conclu que PNMQ est un losange donc <PQM=<PNM =2<ABC CQFD . Sauf erreur . 
Problème 12 :
ABC un triangle Soit ABQP et ACDE deux carrés éxtérieur au triangle soit I le milieu de BC et N et M les point d'intersections des diagonal des carrés MQ le triangle IMN est réctangle et Isocèle en I xD, notre prof Ajerd nous a donné cet exo dans un examen la semaine derniere, ta question était l'avant derniere  | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mar 01 Mar 2011, 20:34 Mar 01 Mar 2011, 20:34 | |
| solution du problème13:- Spoiler:
| |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mar 01 Mar 2011, 20:38 Mar 01 Mar 2011, 20:38 | |
| - majdouline a écrit:
- solution du problème13:
- Spoiler:
C'est plutôt <MPR=180°-<RSC | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mar 01 Mar 2011, 20:56 Mar 01 Mar 2011, 20:56 | |
| - Mehdi.O a écrit:
- majdouline a écrit:
- solution du problème13:
- Spoiler:
C'est plutôt
<MPR=180°-<RSC
??? problème 14:
Soit ABCD un parallélogramme ,M un point de [AB], N de [BC] tel que
AM=CN.On note Q l'intersection de (AN) et (CM) . Mq (DQ) est
bissectrice de < ADC | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mer 02 Mar 2011, 16:51 Mer 02 Mar 2011, 16:51 | |
| - Spoiler:
Solution au problème 14 :  Soit X l'intersection de CM et AD , Z l'intersection de AN et CD et Y l'intersection de AC e de la bissectrice de <ADC . On a d'après le théorème de Thalès+le théorème de bissectrice : 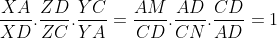 Donc d'après Ceva les droites DY,AZ et CX sont concourantes .. d'où le résultat .
Problème 15 : Soit ABC un triangle rectangle en C . K le projeté orthogonal de C sur AB. La bissectrice de l'angle <ACK coupe [AB] en E . La parallèle à EC passant par B coupe (KC) en F . montrer que (EF) coupe [AC] en son milieu . | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Mer 02 Mar 2011, 22:54 Mer 02 Mar 2011, 22:54 | |
| - Sylphaen a écrit:
Problème 15 :
Soit ABC un triangle rectangle en C . K le projeté orthogonal de C sur AB. La bissectrice de l'angle <ACK coupe [AB] en E . La parallèle à EC passant par B coupe (KC) en F . montrer que (EF) coupe [AC] en son milieu .
- Spoiler:
Soi M l'intersection de (EF) et (AC)
On note x=<ECK ; y=<CAB
On a <KCB+<CBF+<BFC=180 et <ECB+<CBF=180==> <CFB=x
puis on démontre facilement que : <MEC=<EFB et que <KCB=y
on a :
MC=EM sin(<MEC)/sin(x) ; AM=EM sin(<AEM)/sin(y)
d'un autre coté on a
sin(<EFC)/EB=sin(<FEB)/FB=sin(<MEA)/FB=sin(<MEC)/EB ==> sin(<MEC)/sin(<MEA)=EB/FB
aussi on a :
sin(<KCB)/FB=sin(<CFB)/BC==> sin(x)/sin(y)=BC/FB
Il reste a démontrer que EB=BC ce qui est facile car
x+<CEK=90=2x+y==> <CEK=x+y
ce qui achève la preuve
Probleme 16 :SOit ABCDE un pentagone convexe tel que  SOit P l'intersection de (BD) et (CE) Montrer que (AP) Coupe [CD] en son milieu .
Dernière édition par Sporovitch le Jeu 03 Mar 2011, 13:33, édité 1 fois | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Jeu 03 Mar 2011, 12:57 Jeu 03 Mar 2011, 12:57 | |
| Solution au problème 16 : - Spoiler:
 Soit M le milieu de [BC] , F l'intersection de BD et AC et H l'intersection de AD et CE . Alors le problème est équivalent à prouver que les droites DF ,CH et AM sont concourante , ce qui est encore équivalent à ( D'après Ceva ) : 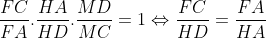 Ce qui est vrai puisque les quadrilatères ABCD et ACDE sont semblables ..
Problème 17 : Soit I a le centre du cercle C a exinscrit à ABC ( tangent au côté [BC] ). Le cercle C a est tangent à AB et AC en B' et C' respectivement .I aB et I aC intersecte B'C' en P et Q respectivement et M est l'intersection de BQ et CP . Prouver que la distance de M à BC est égal au rayon du cercle inscrit au triangle ABC | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Jeu 03 Mar 2011, 23:11 Jeu 03 Mar 2011, 23:11 | |
| solution du problème17: - Spoiler:
on note H le projeté orthogonal de M sur [BC], I a , M et H sont allignés.... on a HCI a et CC'I a sont semblables alors: 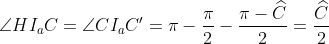 de même , 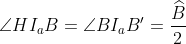 en considérant le triangle B'C'I a (isocèle) on a : }{2}=\frac{\widehat{A}}{2}) 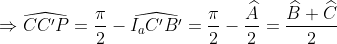 Or : 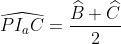 CPI a C' est donc inscriptible d'où: 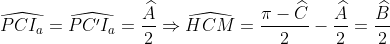 alors : .HC) soit K le point d'intersection du cercle inscrit à ABC et [BC] , on a donc : .BK) et puisque KB=CH on en déduit le résultat voulu.....
problème 18:
Soit ABC un triangle tel que : ∠A = 40° et ∠B = 60°. X un point à l'intérieur du triangle tel que ∠XBA = 20° et ∠XCA = 10°. Montrer que AX est perpendiculaire à BC. | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Ven 04 Mar 2011, 08:28 Ven 04 Mar 2011, 08:28 | |
| - majdouline a écrit:
problème 18:
Soit ABC un triangle tel que : ∠A = 40° et ∠B = 60°. X un point à l'intérieur du triangle tel que ∠XBA = 20° et ∠XCA = 10°. Montrer que AX est perpendiculaire à BC.
- Spoiler:
On note H le projeté orthogonal de A sur [BC]
Il s'ensuit que sin(30)=BH/AB
On note H' le projeté orthogonal de X sur [BC]
Il s'ensuit que : sin(50)=BH'/XB (d'un autre côté on a clairement XB=BC) donc sin(50)=BH'/BC
==> sin (30)/sin(50) = (BH/BH')(BC/AB) et puisque (BC/AB=sin(40)/sin(80)) loi des sinus
donc BH/BH'=sin(30).sin(80)/(sin(50).sin(40))=1
donc BH=BH' ==> H et H' sont confendus
CQFD
| |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Jeu 10 Mar 2011, 22:04 Jeu 10 Mar 2011, 22:04 | |
| Probleme 19 :
Soit un triangle ABC et un point P à l'intérieur de ce triangle tel que
<PAC=<PBC. Les perpendiculaires à (BC) et (AC) pasasnt par P coupent respectivement ces deux droites aux points L et M . Soit D le milieu de [AB]
Montrer que DL=DM | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Ven 11 Mar 2011, 22:39 Ven 11 Mar 2011, 22:39 | |
| Solution du problème 19:Premièrement, nous avons <PAC=<PAM=<PBC=<PBL et les triangles PBL et PAM sont droits, ainsi ils sont semblables, donc <APM=<BPL. D'autre part nous <CMP+<PLC=180° donc le quadrilatère MCPL est inscriptible, ainsi <ACP<MCP=<LPM et <PCB=<PCL=<PML. D'autre part, nous avons sin(<MCP)/AP=sin(<PCB)/BP, et sin(<PLM)/AP=sin(<PML)/BP Donc MP/PL=AP/BP et nous avons <PML=<BAP ainsi les deux triangles ABP et MPL sont semblables, il s'ensuit que <APB=<MPL donc M,P et L sont collinéaires, et A,P et L sont collinéaires ! donc <PMA=<BMA=90°. Maintenant considérons le cercle dont le centre est D, puisque le triangle AMB est rectangle en M, donc [AB] est un diamètre de ce cercle, et pusique le quadrilatère AMLB est inscriptible ( car <BAM+<BLM=90°+<PLM+<BAP+<PAM=90°+<ACP+<BAP+<CAP=90°+1/2(<A+<B+<C))=180°)donc ce cercle passe par M et par L Il s'ensuit que DM=DL. CQFD  | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Ven 11 Mar 2011, 23:05 Ven 11 Mar 2011, 23:05 | |
| - Mehdi.O a écrit:
- Solution du problème 19:
Premièrement, nous avons <PAC=<PAM=<PBC=<PBL et les triangles PBL et PAM sont droits, ainsi ils sont semblables, donc <APM=<BPL.
D'autre part nous <CMP+<PLC=180° donc le quadrilatère MCPL est inscriptible, ainsi <ACP<MCP=<LPM et <PCB=<PCL=<PML.
D'autre part, nous avons sin(<MCP)/AP=sin(<PCB)/BP, et sin(<PLM)/AP=sin(<PML)/BP
Donc MP/PL=AP/BP et nous avons <PML=<BAP ........................ bonsoir  pour ce qui est en gras ..on l'a pas  | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Ven 11 Mar 2011, 23:10 Ven 11 Mar 2011, 23:10 | |
| - majdouline a écrit:
- Mehdi.O a écrit:
- Solution du problème 19:
Premièrement, nous avons <PAC=<PAM=<PBC=<PBL et les triangles PBL et PAM sont droits, ainsi ils sont semblables, donc <APM=<BPL.
D'autre part nous <CMP+<PLC=180° donc le quadrilatère MCPL est inscriptible, ainsi <ACP<MCP=<LPM et <PCB=<PCL=<PML.
D'autre part, nous avons sin(<MCP)/AP=sin(<PCB)/BP, et sin(<PLM)/AP=sin(<PML)/BP
Donc MP/PL=AP/BP et nous avons <PML=<BAP ........................ bonsoir 
pour ce qui est en gras ..on l'a pas  Oui, en effet, c'est parce que je l'ai vu dans ma figure et j'ai cru que c'était trivial. Bon je vais essayer de démontrer cette condition, sinon ce qui reste est juste? | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  Ven 11 Mar 2011, 23:24 Ven 11 Mar 2011, 23:24 | |
| Bon dans le cas où P est l'intersection de (AL)et (BM) c'est résolu, il reste l'autre cas, je vais le traiter demain.
Maintenant je suis fatigué ! | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Marathon De Géométrie Sujet: Re: Marathon De Géométrie  | |
| |
|
  | |
| | Marathon De Géométrie |  |
|
