Préparation dernière phase 2012.

Bonsoir tout le monde , en vue de l'approche , de la dernière phase des olympiades , on a décidé de créer ce sujet , histoire de se préparer tous ensembles , les problèmes proposé porteront sur : la géométrie , inégalité , arithmétique et équations fonctionnels . Il n'y a pas de changement concernant les règles , tous le monde sur le forum peut participer . On commence avec le problème suivant.

Solution au problème 1:
Soit I l'intersection de (AC) et (BD),
on a (AD)//(BE) donc par Thalès: .
De même: (AF)//(BC), donc: .
Il s'en suit que: , d'où: (CD)//(EF) (par la réciperoque de Thalès dans le triangle IEF).


Problème 2:
Soient a_1, a_2, ... , a_n des réels strictement positifs. Montrer que:

ali-mes a écrit:

Problème 2:
Soient a_1, a_2, ... , a_n des réels strictement positifs. Montrer que:

n=1

Bonjour , Bravo pour ta réponse au probléme 1 , concernant ton inégo elle est clairement fausse par exemple a_i=1 et n=1

diablo902 a écrit:

n=1

D'où l'exercice est tiré, il n'y a pas des informations sur n, mais j'assume que n>1.
Merci pour votre vigilance !

ali-mes a écrit:

diablo902 a écrit:

n=1

D'où l'exercice est tiré, il n'y a pas des informations sur n, mais j'assume que n>1.
Merci pour votre vigilance !

Et pour n=2 ?
ton problème est faux ! Prière de le changer

diablo902 a écrit:

ali-mes a écrit:

diablo902 a écrit:

n=1

D'où l'exercice est tiré, il n'y a pas des informations sur n, mais j'assume que n>1.
Merci pour votre vigilance !

Et pour n=2 ?
ton problème est faux ! Prière de le changer

C'est édité

la premiere inegalité il la manque un carré : (n²+2012)² !!!

az360 a écrit:

la premiere inegalité il la manque un carré : (n²+2012)² !!!

Oui, c'est ça ! Je m'excuse pour la faute ... Je vais éditer l'inégalité initiale , et je vais poster la deuxième inégalité (pour ceux intéressés) dans la section ''Inégalités''.

.

.

boubou math a écrit:

Maintenant avec C.S:

ton inégalité sera inversée lorsque tu vas multiplier !

Edit.

solution du Problème 2: on peut supposé que \sum(a_i)=1 , en multipliant les deux cotés par : n^3+1 , et en appliquant C-S au membre de gauche , sachant que : n^3+1=(n²+...+n²) +1 , l'inégalité revient a prouver , on posant x=\sum(1\ai) , et a=2012 .que (n²+a)(nx+1) >= (n^3+1)(x+a) , équivalant a (X-n²)(an-1) >=0 ce qui est clairement vrai , puisque , n>=1 et x>= n² (par AM-GM) .

Problème 3: soient des réels x,y,a et b tel que : , et , Démontrer que : .

Solution au problème 3:

Si 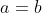, alors: , donc: .
Si , Donc: , d'où: .
Donc: .

Problème 4:
On colorie tous les carreaux d'un tableau 3x7 avec deux couleurs. Montrer qu'on peut toujours trouver un rectangle dont les coins sont coloriés par la même couleur.

ali-mes a écrit:

Problème 4:
On colorie tous les carreaux d'un tableau 3x7 avec deux couleurs. Montrer qu'on peut toujours trouver un rectangle dont les coins sont coloriés par la même couleur.

Je propose une solution:
Puisqu'on utilise 2 couleurs pour colorier 21 carreaux d'un rectangle, on peut confirmer qu'au moins 11 carreaux sont de la même couleur.
Et puisque 11=7+4, on déduit que ces carreaux ne sont pas sur la même ligne (notre rectangle est composé de 3 lignes dont chacun a 7 carreaux).
Ainsi, on peut toujours trouver un rectangle qui satisfait la condition...
Sauf erreurs.
P.S: J'attends une confirmation.

Je vois que c'est juste... A toi de proposer !

Je continue avec un exercice facile:
Problème 5:
Soient a, b et c les mesures des côtés d'un triangle ABC.
On construit un triangle A'B'C' tel que ses côtés mesurent , et .
Démontrez que
Bonne chance.

une application direct de Héron le tue

Solution au problème 5:
Soit p' le demi périmètre du triangle A'B'C', donc: .
D'après la formule de Héron:


En utilisant la transformation de Ravi (avec a=x+y, b=y+z et c=x+z), on obtient:


Et on a: .
Donc:

.
Et on a d'après l'IAG:

Le produit de ces trois inégalités, en tenant compte de la positivité des termes, donne le résultat voulut.

Problème 6:
Soient x,y et z des réels strictement positifs. Montrer que:
.

problème 6 : par symétrie l'inégalité de réordonement nous donne : , (somme cyclique ) , ainsi il suffit de montrer que chaque somme vérifie : (2) , ce qui nous permetra de conclure par sommation , or , ainsi en trouve le LHS de (2) : d'ou le resultat , l'autre inégo ce fait de la même façon .

Problème 7 Trouver tout les entier naturels vérifiant la propriété suivante : s'il existe Trois réel positif a,b,c tel que leurs somme est égale a 3 , alors :

Oty a écrit:

Problème 7 Trouver tout les entier naturels vérifiant la propriété suivante : s'il existe Trois réel positif a,b,c tel que leurs somme est égale a 3 , alors : .

Ce problème est difficile, n'est ce pas?
Cependant, on remarque à l'aide de l'inégalité de Chebychev que si n est solution alors n+1 l'est également.
Du fait, la question qui doit être posée est "trouvez la valeur minimale de l'entier naturel n tel que qu’on ait la propriété...".
Personnellement, je n'ai plus de solution. Mais une chose est certaine, si n est solution alors n est supérieur ou égal à 4.
(on remarque trivialement que n=1 et n=2 ne conviennent pas, le couple (1,3/2,1/2) élimine le cas n=2 et le couple (2,1/4,7/4) élimine le cas n=3).
Au plaisir!