Le dernier jeu pour la préparation aux IMOs 2012:

Je crée cette page afin de préparer les olympiades internationales et les étapes qui reste des olympiades nationales.
A l'instar d'un ancien jeu, la participation aura comme règles:
§Les exercices doivent être dans les divers piliers des olympiades. Et pour donner une ambiance pour le jeu, les problèmes doivent respecter le cycle suivant:
équations fonctionnelles+inégalités+géométrie+arithmetiques+combinatoires+géometrie, et ainsi de suite.
§Si on ne parvient plus à résoudre un problème, dans un délai de 48 heurs, il sera modifié.
§Ne pas poster d'hors sujets.
Je termine par deux remarques:
§La participation est ouverte pour tout le monde, surtout ceux qui se préparent pour le deuxième stage.
§Il faut que la solution soit lisisble même si elle n'est pas rédigée en Latex.
On commence maintenant.
Bonne chance.

Problème 1:
Soient f et g deux fonctions dérivables et non-constantes sur tel que:
.
Montrez que .
Bonne chance.

rien dit .

Oty a écrit:

l'exercice est erroné , contre exemple : et .

Effectivement, tu as raison.
Et pourtant, il s'agit du quatrième exercice du premier test du baccalauréat de l'an 2008.
Trouver un contre exemple mérite un travail dur, bravo.
L'exercice sera modifié, en effet la troisième condition doit être et non . Ainsi que les deux fonctions doivent être non-constantes.
Désolé.

nmo a écrit:

Problème 1:
Soient f et g deux fonctions dérivables et non-constantes sur tel que:
.
Montrez que .
Bonne chance.

Le délai est terminé sans qu'aucun membre ne présente sa solution, je présente la mienne:
Calcul de f(0) et de g(0):
Si on prends x=y=0 dans les deux relations de l'énoncé, il vient que et .
C'est à dire que et .
La seconde relation implique que ou .
Démontrons la fausseté de par l'absurde.
En effet, si , on aura de la première relation. Ce qui apporte la contradiction désirée.
Ainsi, il résulte que .
On tire immédiatement .
Utilisation de la dérivabilité:
La première relation implique que .
Et si y est différent de 0, on écrit .
En faisant tendre y vers 0, on aura .
On use de la troisième condition pour aboutir à . (1)
De même, on aura . (2)
Démonstration du résultat:
Soit h la fonction définie sur par .
La fonction h est clairement dérivable sur son ensemble de définition, et on a .
Donc , en utilisant 1 et 2.
Ainsi la fonction h est constante, et par conséquent .
Et ainsi , en utilisant f(0)=1 et g(0)=0.
CQFD.
Sauf erreur.

Je propose de nouveau un exercice, qui traitera une inégalité:
Problème 2:
Soient a, b et c trois réels vérifiant la condition suivante: .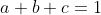
Montrez que .
Bonne chance.
P.S: J'ai l'impression que je continuerai de jouer tout seul...

Oty a écrit:

Bonsoir , je propose , il est bien connue que : et , on pose : et , on obtient et (d’après la condition ) , d'ou . Ainsi il suffit de prouver que : , une rapide étude ce trinôme second degrés montre qu'il s'écrit : avec (x1 et x2 sont connue ) d'ou le résultat , sauf erreur...

Non, ce que tu avances est faux, jette un coup d'oeuil ici: http://www.wolframalpha.com/input/?i=16x%5E2-46%2F3+x%2B1.
Essaie autrement.

oui effectivement j'ai fais une erreur de calcule ....

nmo a écrit:

Je propose de nouveau un exercice, qui traitera une inégalité:
Soient a, b et c trois réels vérifiant la condition suivante: .
Montrez que .
Bonne chance.
P.S: J'ai l'impression que je continuerai de jouer tout seul...

Pose (a,b,c)=(1/3,1/3,1/3) ou (0,1/2,1/2)

oui diablo a raison

Oty a écrit:

oui diablo a raison

Il emblerait que je ne choisi que les fausses exercices.
Je m'excuse, et je propose donc un exercice d'inégalité que j'ai traité:
Problème 2:
Soient 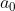, 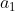,... et 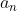des nombres réels de l'intervalle ]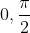[ tels que .
Montrez que .
Bonne chance.

probleme 2 :
solution :
l'inegalité est equivalente a celle-cii : .
d'autre part on a : 1-a_{0} >= a_{1} + ... + a_{n} >= n*sqrt[n](a_{1}...a_{n})
on fait la meme chose pour les autres . d'ou le resultat .

problem 3:
ABC triangle . soit P a l'interieur de ABC tel que : <BPC = 180 - <ABC et CP\PB = CB\AB
montrer que : <APB = <CPB

bonsoir , @Az , j'ai rien compris a ta démo ^^ , tu peux préciser un peu plus ? Merci .

Oty a écrit:

bonsoir , @Az , j'ai rien compris a ta démo ^^ , tu peux préciser un peu plus ? Merci .

Sa solution est très réduite, et pourtant elle est très bonne.
Il a suivi la démarche suivante:
Simplifier en utilisant la loi des tangentes, pour obtenir .
Puis, il a posé , pour chaque i compris entre 1 et n.
Et finalement, il a utilisé astucieusement l'inégalité arithmético-géométrique.

az360 a écrit:

problem 3:
ABC triangle . soit P a l'interieur de ABC tel que : <BPC = 180 - <ABC et CP\PB = CB\AB
montrer que : <APB = <CPB

C'est facile et simple, voici ma démonstration:
On a , ce qui s'écrit ou bien .
D'où .
Et puisqu'on a , il s'ensuit que les deux triangles PCB et PBA sont directement semblables.
Du fait, leurs angles opposés ont la même mesure. Le résultat en découle immédiatement.
Sauf erreur.

ouiii nmo a toi de proposer !!!

Le tour est maintenant de l'arithmétique:
Problème 4:
Soit la suite définie par: .
Montrez qu'il y a au moins mille fois le chiffre 9 dans l'écriture décimale de .
Bonne chance.

solution pour 4:
voila nous poson : b_n = u_n + 1.
on a : b_{n+1} = 4(b_n - 3)(b_n)²
alors on peut montrer par une simple reccurence que : 10^{2^{n}} divide b_n
parce que : 100 divide b_1 ...
alors on aura que : 10^{2^10} divide b_10
d'autre part on a : 2^10 > 1000 (difference de 24 ..)
alros : u_10 aura au moins mille fois le chiffre 9 ...

Spoiler:

probleme 5 :
resoudre dans R cette systeme :
x+y² = y^3
y + x² = x^3 .
bonne chance .

je crois l'avoir résolue je rédige ... on faisant la différence des deux égalité on obtient : soit : x=y ou le discriminant de la 2eme équation (en gardant y fixe et x variable ) est : d'ou la seul possibilité est : x=y : on remplace dans le l'équation on trouve : x=0 ou x²-x-1=0 de la il est facile de trouver les solutions ...

Problème 6 : Soit un triangle ABC isocèle en 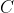. D et E sont deux points des cotes AC et BC de tel manière que les bissectrice des angles et se coupent sur le segment AB en F . Montrer que F est le milieu du segment AB .

Oty a écrit:

je crois l'avoir résolue je rédige ... on faisant la différence des deux égalité on obtient : soit : x=y ou le discriminant de la 2eme équation (en gardant y fixe et x variable ) est : d'ou la seul possibilité est : x=y : on remplace dans le l'équation on trouve : x=0 ou x²-x-1=0 de la il est facile de trouver les solutions ...

Le discriminent est bel et bien faux, mais la démarche est bonne ainsi que les solutions trouvées vers la fin.
C'est à ton tour de proposer un exercice soit de combinatoires ou de géométrie.

Bon je l'ecrit autrement : [img]http://latex.codecogs.com/gif.latex?\Delta=-3y^2&plus;2y-3=-3[(y-\frac{1}{3})^2&plus;\frac{8}{9}]&space;<&space;0[/img]

solution du probleme 6 :
on a d'apres le loi de sin dans les deux triangles EBF et DFA
: EF*sin(x)*AF = DF.FB.sin(y) (1)
d'ou x = <DEF et y = <EDF
alors : FB = FA <=> EF\DF = sin(y)\sin(x)
ce qui bien loi de sin dans le triangle DEF . d'ou le resultat .